Da-Wei Ding(丁大為)Fang-Fang Liu(劉芳芳)Hui Chen(陳輝)Nian Wang(王年)? and Dong Liang(梁棟)

1Key Laboratory of Intelligent Computing and Signal Processing,Ministry of Education,Anhui University,Hefei 230601,China

2School of Electronics and Information Engineering,Anhui University,Hefei 230601,China

1 Introduction

Leon Chua predicted that there should be a fourth type of electronic components,the memristor,based on the physics symmetry.[1]The memristor was not developed or researched within circuit theory until 2008,when HP’s Stan Williamset al.created a solid-state implementation of the memristor.[2]Many studies on the memristor for application development have been published now,such as the memristor-based circuits[3?4]and memristor oscillators.[5?6]

In recent years,more and more scholars are interested in the fractional-order system.In Ref.[7],for the purpose of investigating the nonlinear dynamics of the system,a fractional-order Chua’s circuit based on the memristor,which derives from the integer-order counterparts was provided.The fractional-order system is widely applied in many aspects,such as the oscillator theory,[8]the control field,[9?11]and the energy field.[12]Some of the classic systems have been extended to their fractionalorder counterparts,for example,the Liu system,[13?14]the Chen system,[15]the Duffing system,[16]and the viscoelastic system.[17]

Time delay exists in many engineering systems,causing system instability and bad performance.And it is unavoidable in many dynamical systems,such as biological systems,[18]neural networks,[19]system control,[20]and so on.Therefore,it is signi ficant to investigate the timedelayed effect on dynamical behaviors of complex systems theoretically and practically.

Furthermore,the fractional-order delayed system involves non-integer order derivatives as well as time delay.These have been proved useful in financial system,[21]signal processing,[22]biology,[23]and so on.Many researchers have studied the fractional-order delayed system.[24?29]In Ref.[28],the bifurcation in Duffing-van der Pol oscillators with time delay was analyzed.In Ref.[29],the bifurcation and stability in three neurons fractional-order neural network were investigated by applying the sum of time delay as the bifurcation parameter.Additionally,chaos behaviors in the fractional-order delayed system have become the key focus.[30?31]In Ref.[30],the chaos in a delayed Bloch model was discussed and found that time delay can affect the system stability in this system.In Ref.[31],the discrete chaotic dynamics in fractional delayed logistic maps was studied,and the discrete chaotic attractor was discovered.In Ref.[32],we have analyzed the stability and Hopf bifurcation of fractional-order delayed memristor-based chaotic system by choosing the time delay and fractional-order as the bifurcation parameter.

Chaotic control is to make the trajectories of initial chaotic system approach a steady state.Many control schemes for fractional-order chaotic systems have been proposed,including active control,[33]impulsive control,[34]adaptive control,[35]passive control[36]and generalized projective control.[37]Sliding mode control has received much attention due to its major advantages such as robustness against parameter variations,guaranteed stability,simplicity in implementation and fast dynamic response.Therefore,in recent years,sliding mode control has been investigated for linear and nonlinear systems.[38?41]Many vital results have been reported for the synchronization and control of fractional-order chaotic systems by using the sliding mode control strategy.In Ref.[42],to realize complete synchronization of a class of three-dimensional fractional-order chaotic systems,the author modi fied sliding mode control scheme,and designed a single-state sliding mode controller.In Ref.[43],Tanmoy Dasguptaet al.proposed a novel fractional-order sliding mode controller for synchronization of fractional order chaotic systems,and achieved its application in secure communication.The scholars studied the adaptive sliding mode synchronization control for a class of fractional-order chaotic systems with unknown bounded disturbances in Ref.[44].In order to achieve finite time convergence of the system states,a terminal sliding mode control method was firstly proposed by Zak in Ref.[45].In Ref.[46],the terminal sliding mode control technique that offers some superior properties such as fast response and finite time convergence was proposed,which is particularly suitable for high-precision control as it speeds up the rate of convergence near the origin.In Ref.[47],they investigated the chaotic control of a class of fractional-order chaotic systems via sliding mode control.In Ref.[48],the authors derived new results based on the sliding mode control for the anti-synchronization of four-wing chaotic systems.

Motivated by aforementioned analysis,the main purpose of this paper is to design a fractional-order sliding mode controller,which is the combination of fractional calculus theory and the sliding mode control technique in order to control the fractional-order delayed memristive chaotic system.For this purpose,sliding mode control scheme is utilized along with Lyapunov stability theory to design the suitable control structure.Recall that slide mode controllers,which applied to the fractionalorder chaotic system may be numerous,while applied to fractional-order delayed memristor system are few.The proposed controller makes the system states asymptotically stable and robust against the system’s uncertainty in the presence of an external disturbance.Simulation results illustrate that the proposed method can eliminate chaos and stabilize the system in a finite time.

The rest of this paper is organized as follows.In Sec.2,we discuss a fractional-order delayed memristive chaotic system.According to the sliding mode control theory,a controller is proposed to control the commensurate and non-commensurate fractional-order delayed chaotic system in Sec.3,the design procedure of fractional-order sliding mode approach is described in this section.Numerical simulations results are shown in Sec.4.Finally,some conclusions are drawn in Sec.5.

2 System Description

A memristor is a passive two-terminal circuital element,and it is described by a nonlinear characteristic:iM=W(φ)vM,vM=M(z)iM,whereiM,vM,φ,andzare the current,the voltage,the flux,and the charge in memristor.W(φ)=dz(φ)/dφandM(z)=dφ(z)/dzexpress as inductance and memristance respectively.

Furthermore,the relationship ofφ(z)andz(φ)can be de fined with the charge-controlled memristor and fluxcontrolled memristor.We choose the flux-controlled memristive system:

whereiMandvMdescribe the current and the voltage through the memristor,andf(t,x,vM)is the internal state function.

De finition 1(Ref.[49]):In this paper,a continuous functionf:R+→Rrepresents the Caputo fractional derivative,which has a fractional-orderq:

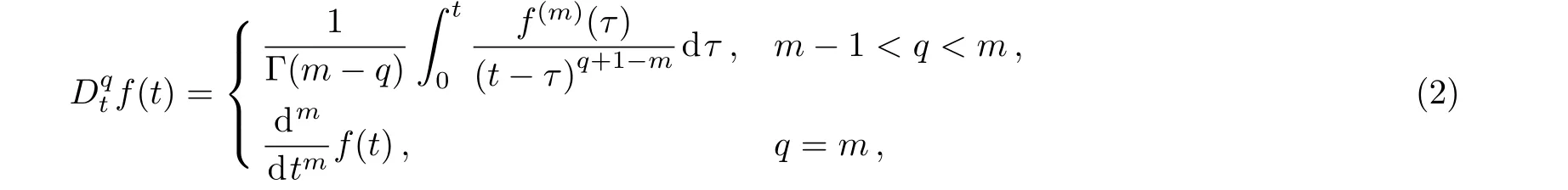
where Γ(q)is the gamma function,m?1＜q≤m,m∈N.

The simplest delayed memristive chaotic system includes a resistorR,a voltage followerU2,a capacitorC,a flux-controlled memristorM,a time delay unit,and an integratorU1(Fig.1 in Ref.[50]).The following equations describe the delayed memristive chaotic system in Fig.1.

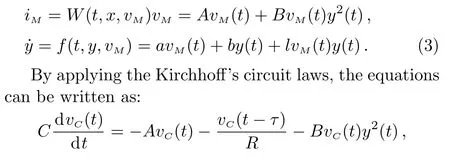
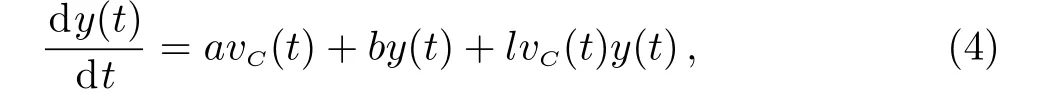
whereτis the time delay,yis the state variable of the memristor,andA,B,a,bandlare the constants.

From the integer-order system,we derive the equations of the fractional-order memristive system,and it can be calculated as:

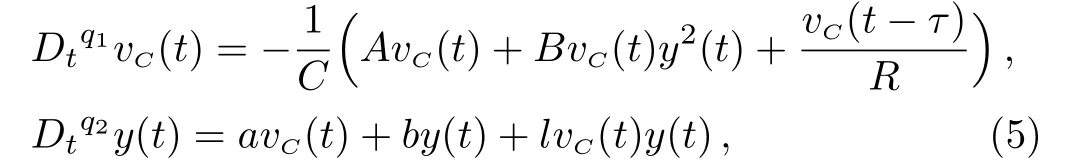
whereq1andq2are the fractional-order of the capacitorCand memristorM.

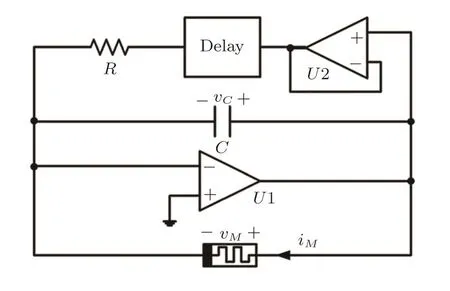
Fig.1 Model of the delayed memristive chaotic system.

Then,we get the following equations:

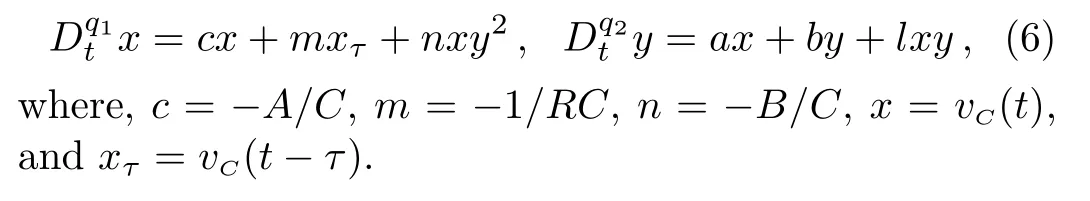
3 Designing the Sliding Mode Control

We add the control inputu(t)to the state equations in system(6)to control the chaos behavior:

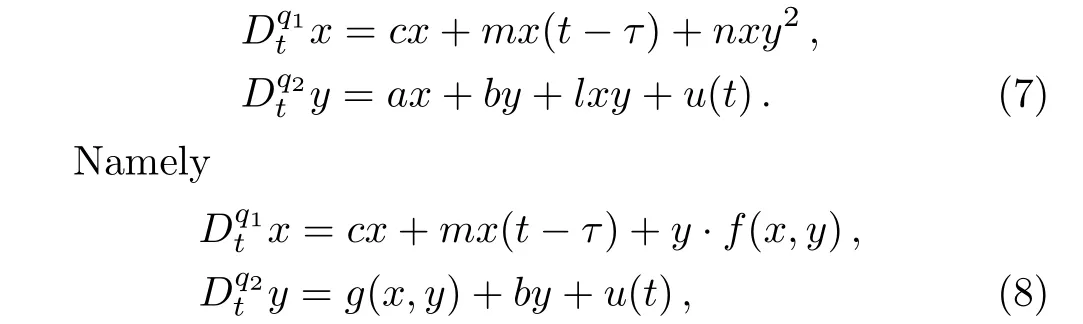
where,f(x,y)=nxy,g(x,y)=ax+lxyis assumed.

Our aim is to design a fractional-order sliding mode controller.The first step is constructing a fractional-order sliding surface that represents a desired system dynamics.Then,a switching control law should be developed,and any states outside the surface are driven to reach the surface in a finite time.[51]Therefore,we choose a sliding surface:

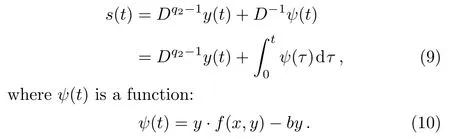
According to the sliding mode method,the sliding surface and its derivative must satisfy the following conditions:

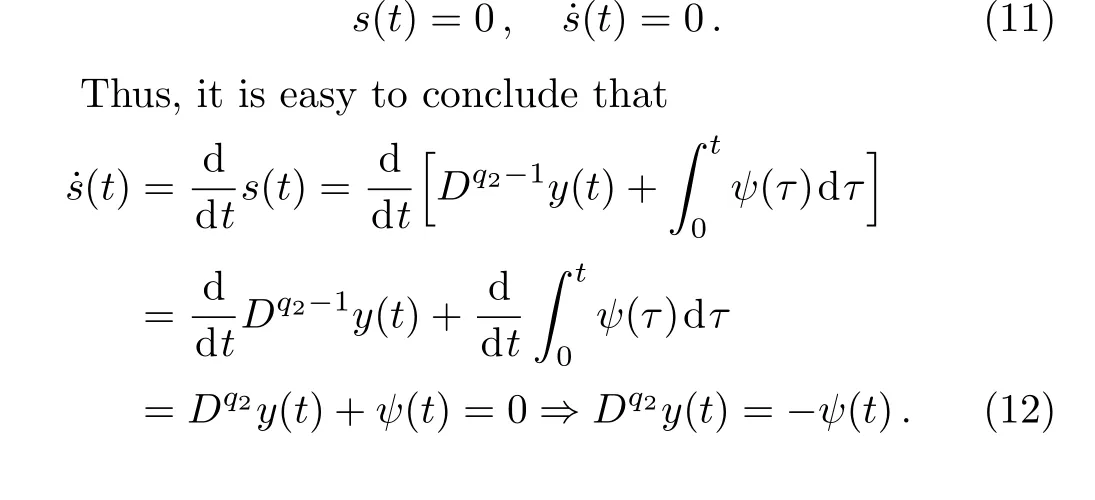
The equivalent control law is calculated as:

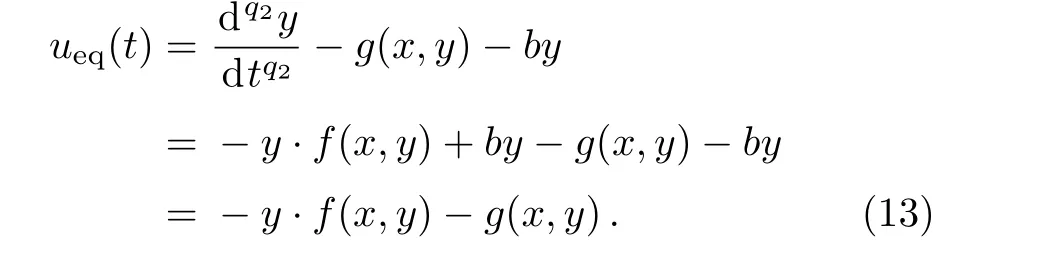
The switching control can keep the system within the sliding manifold.To satisfy the sliding condition,the discontinuous reaching law is chosen as follows:

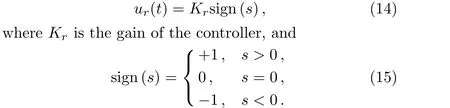
Therefore,the total control law can be de fined as:

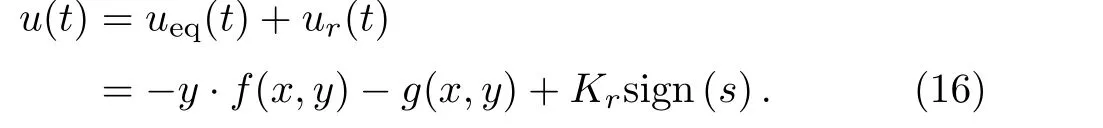
Theorem 1Considering the fractional-order delayed memristive chaotic system(8),and the control law(16),if the controller gainKr＜0,the system is asymptotically stable.

ProofThe Lyapunov candidate is selected as:

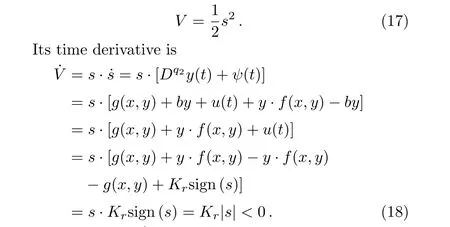
WhenKr＜0,˙V＜0 fors(t)/=0.In other words,the controlled system satis fies the reaching condition.Therefore,a Lyapunov function has been found that it satis fies the conditions of the Lyapunov stability theorem(V＞0,˙V＜0).Thus,the closed-loop system in the presence of the controller(16)is globally asymptotically stable.

Theorem 2Considering the system(8)being perturbed by uncertainties and an external disturbance,it can be modeled as follows:

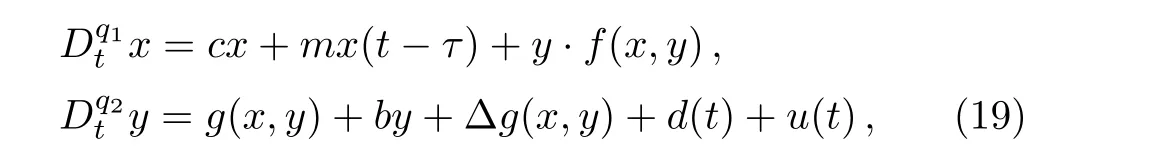
where Δg(x,y)andd(t)are assumed to be bounded,i.e.|Δg(x,y)|≤e1and|d(t)|≤e2.The closed-loop system with the sliding mode control(16)is globally asymptotically stable whenKr＜?(e1+e2).

ProofSelecting the Lyapunov candidate(17),we have

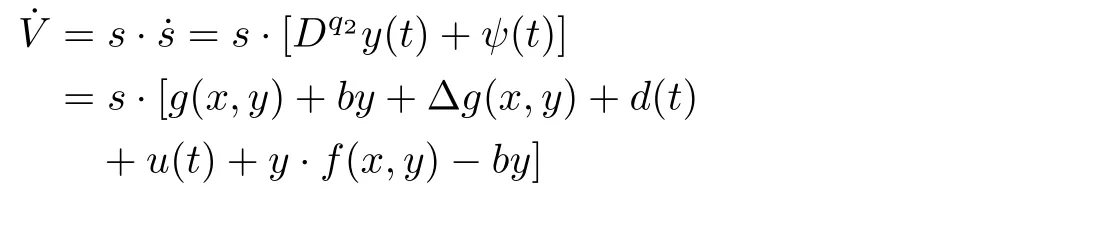
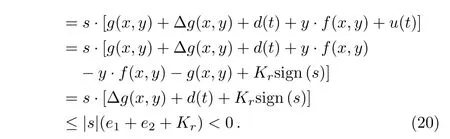
Therefore,in view of the uncertainty and external disturbance,when the controller gainKr＜?(e1+e2),the controller(16)can make the system states asymptotically stable in limited time.

Thus,the theorem is proofed completely.

4 Numerical Simulation

The chaotic states and dynamical behaviors of the uncontrolled system(6)have been discussed in Ref.[50].This section of the paper presents four illustrative examples to verify and demonstrate the effectiveness of the proposed control scheme.In this paper,the modi fied Adams–Bashforth–Moulton predictor-corrector algorithm[52]is used to solve the numerical simulations in the fractionalorder differential equations with time delay.It should be noticed that the controller is applied att=15 s.Here,some parameters are given to calculate in the system:a=2.5b=?0.5,l=?5,c=1.5,m=?2,andn=?2.

Case 1Non-commensurate order

When assuming the different orders of derivatives in state equations(6),i.e.q1/=q2,we get a general noncommensurate order system.The fractional-order delayed memristive chaotic system is chaotic whenq1=0.88 andq2=0.98,which are shown in Fig.2.

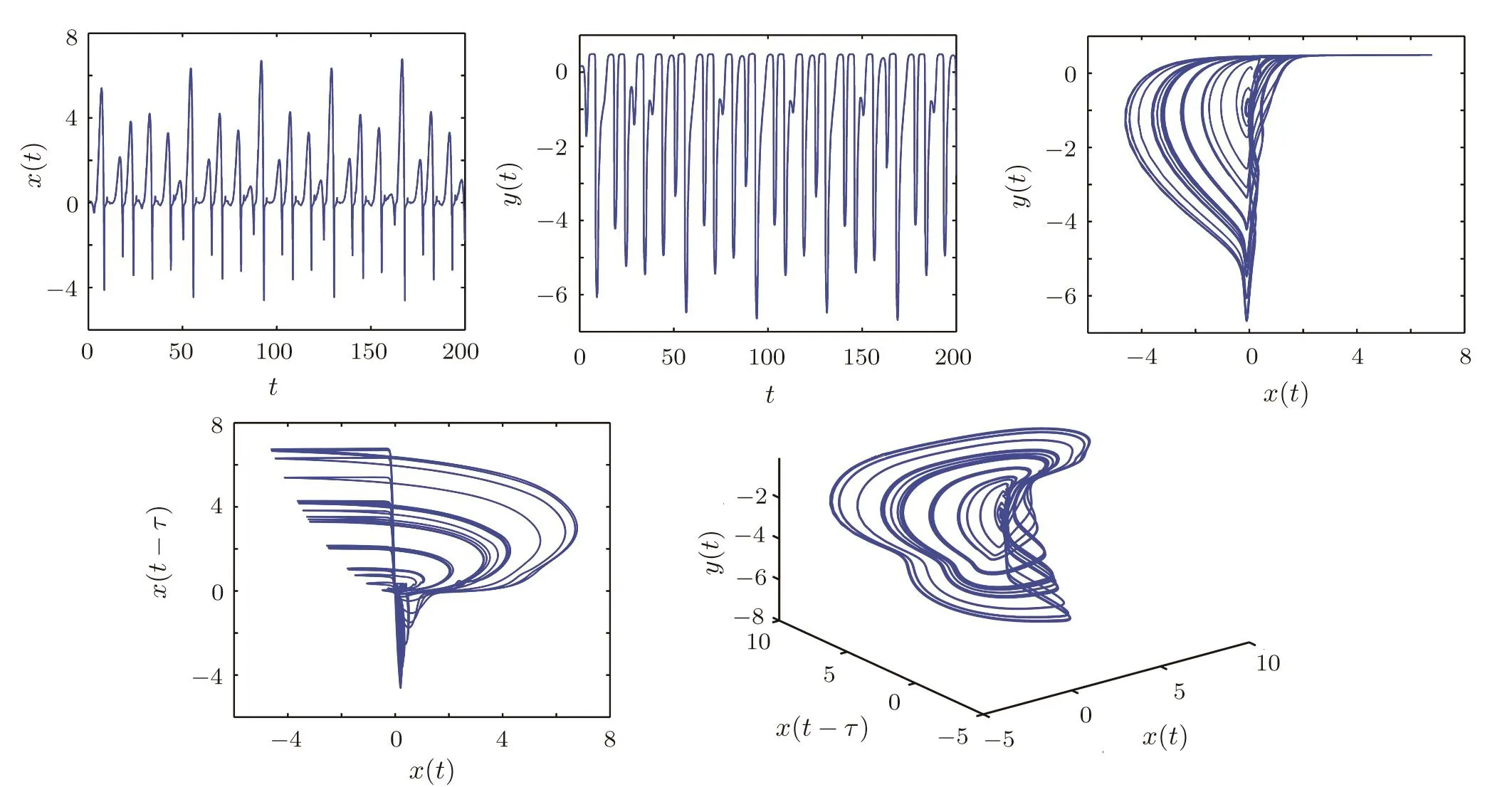
Fig.2 Time-domain diagram and phase diagram of the fractional-order system(6)when q1=0.88,q2=0.98,τ=1.5 without controller.

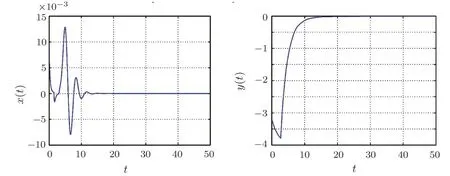
Fig.3 Time response of controlled non-commensurate fractional-order system states(The control u(t)is activated at t=15 s).

In order to satisfy the condition in Theorem 1,we select the gain of the controllerKr=?1 in system(8).To stabilize this system,the control law(16)is applied and the simulation results are depicted in Fig.3.It shows the obtained theoretic results are feasible and efficient for the controlling fractional-order delayed memristive system.

Case 2Non-commensurate order with uncertainty and an external disturbance

In this case,the fractional-order delayed memristive chaotic system is perturbed by an uncertainty term Δg(x,y)=0.45sin(πx)cos(πy)and an external disturbanced(t)=0.5sin(πt),where|Δg(x,y)|≤e1=0.45 and|d(t)|≤e2=0.5.The system state responses of the closed-loop system in the presence of the control law(16)are shown in Fig.4 when the gain of the controllerKr=?1,which conforms to the condition of Theorem 2.

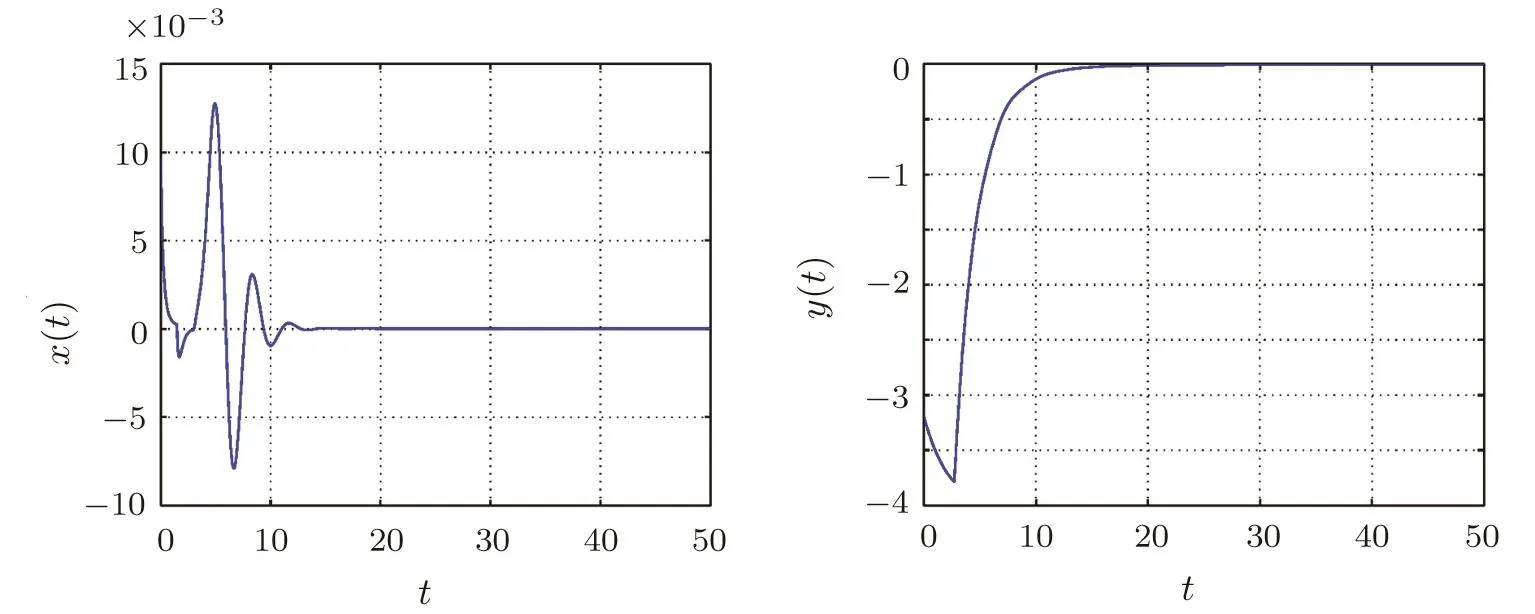
Fig.4 Time response of controlled non-commensurate fractional-order system states in the presence of uncertainty and an external disturbance(The control u(t)is activated at t=15 s).

Case 3Commensurate order

When assuming the same orders of derivatives in the state equations(6),i.e.,q1=q2=q,we get a commensurate order system.The system(6)without the controller exhibits a chaotic behavior as shown in Fig.5 with the commensurate orderq=0.99 of the derivatives.

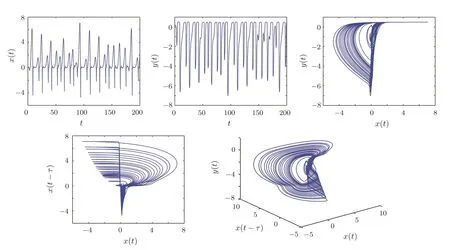
Fig.5 Time-domain diagram and phase diagram of the fractional-order system(6)when q1=q2=0.99,τ=1.5 without controller.

To demonstrate the chaotic behaviors,the Largest Lyapunov Exponent(LLE)should be considered.In this paper,the Wolf algorithm is chosen to calculate LLE in this fractional-order delayed memristive chaotic system.It is known that the Max Lyapunov Exponent(MLE)increases from the negative number to zero when periodic cycles appear,and the chaotic dynamics occurs when MLE is positive.By fixing the parameter of the fractional-order(q=0.9)and varying the parameter of the time delay(τ∈[0.4,1.6]),the transitions from one cycle to two cycles,two cycles to four cycles,and four cycles to chaos are observed atτ=1.18,τ=1.27,andτ=1.28.In the interval 0.54＜τ＜1.18,one cycle is observed.Chaos is observed in the intervalτ＞1.28.The bifurcation diagram and the MLE are shown in Fig.6.

The states of the system(6)under the designed controller(16)are illustrated in Fig.7 whenKr=?1,which shows that the sliding control law guarantees the states reaching the sliding surface and finally stabilization.

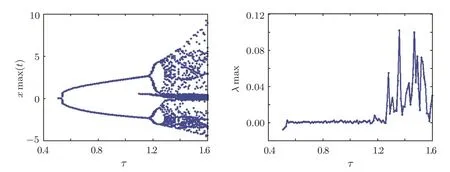
Fig.6 Bifurcation diagram and Max Lyapunov Exponent with q=0.9.

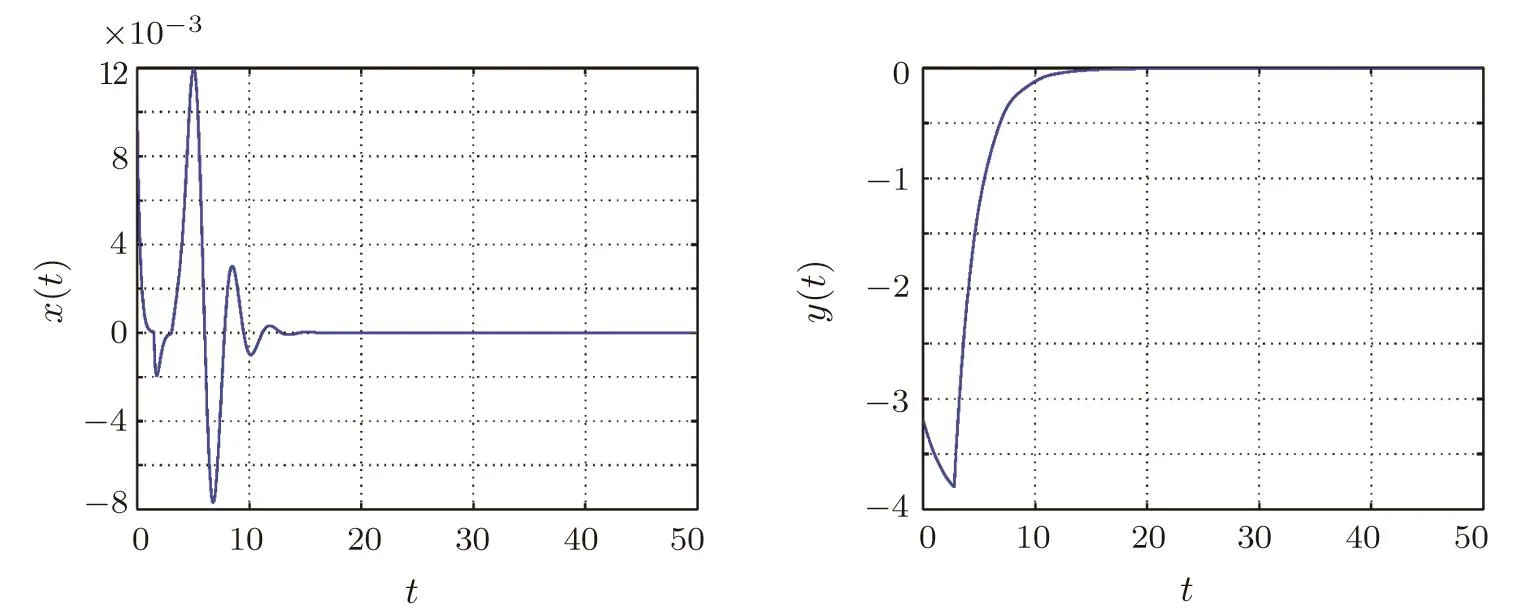
Fig.7 Time response of controlled commensurate fractional-order system states(The control u(t)is activated at t=15 s).

Case 4Commensurate order with uncertainty and an external disturbance

Fig.8 Time response of controlled commensurate fractional-order system states in the presence of uncertainty and an external disturbance(The control u(t)is activated at t=15 s).

In this case,the fractional-order delayed commensurate system(q=0.99)is perturbed by an uncertainty term Δg(x,y)=0.45sin(πx)cos(πy)and an external disturbanced(t)=0.5sin(πt),where|Δg(x,y)|≤e1=0.45 and|d(t)|≤e2=0.5.The system state responses of the closed-loop system in the presence of the control law(16)are illustrated in Fig.8 whenKr=?1,which satis fies Theorem 2.

5 Conclusions

In this paper,a fractional-order delayed memristive chaotic system has been introduced and a fractional-order sliding mode controller is proposed in order to control the chaotic behavior in the system. According to the Lyapunov stability theorem,the control law can asymptotically stabilize the fractional-order delayed memristive chaotic system.The proposed control method is simple,robust and theoretically rigorous,and its performance is satisfactory in the presence of uncertainty and an external disturbance within non-commensurate order system and commensurate order system.It indicates that the sliding mode control has the anti-jamming capability.Finally,numerical simulations present the effectiveness of the control scheme.

Considering that the current system research is not perfect,these studies tend to be more numerical simulation of the system,and did not develop to realize the hardware circuits.In the future,we should focus on how to construct chaotic hardware circuits with associated delay factors.

[1]Leon O.Chua,IEEE Trans.Circuit Theory 18(1971)507.

[2]D.B.Strukov,G.S.Snider,D.R.Stewart,and R.S.Williams,Nature(London)453(2008)80.

[3]B.Muthuswamy and P.P.Kokate,IETE Tech.Rev.26(2009)417.

[4]I.Vourkas and G.C.Sirakoulis,IEEE Trans.Nanotechnol.11(2012)1151.

[5]Makoto Itoh and Leon O.Chua,Inter.J.Bifurcat.Chaos 18(2008)3183.

[6]Corinto,Fernando,A.Ascoli,and M.Gilli,IEEE Trans.Circuits Syst.I,Reg.Papers 58(2011)1323.

[7]D.W.Ding,S.J.Li,and N.Wang,Dynamic Analysis of Fractional-Order Memristive Chaotic System,J.Harbin Inst.Tech.(2017);doi:10.11916/j.issn.1005-9113.16136.

[8]Abbas,Syed,V.S.Erturk,and S.Momani,Signal Process.102(2014)171.

[9]A.K.Golmankhaneh,R.Are fi,and D.Baleanu,J.Vib.Control.21(2002)85.

[10]Girejko,Ewa,and E.Pawluszewicz,J.Dynam.Control Syst.(2016)1.

[11]Kamaljeet and D.Bahuguna,J.Dyn.Control Syst.22(2015)1.

[12]Xu Beibei,et al.,Nonlinear Dynam.81(2005)19.

[13]J.G.Lu,Phys.Lett.A 354(2006)301.

[14]A.K.Golmankhaneh,R.Are fi,and D.Baleanu,Adv.Math.Phys.2013(2013)84.

[15]C.Li and G.Chen,Chaos,Solitons and Fractals 22(2004)549.

[16]J.Cao,C.Ma,H.Xie,and Z.Jiang,J.Computat.Nonlinear Dynam.(2010);doi:10.1115/1.4002092.

[17]Xu,Yong,Y.Li,and D.Liu,J.Comput.Nonlinear Dynam.9(2014)031015.

[18]Gui-Quan Sun,et al.,Sci.Rep.5(2015)11246.

[19]Chang-Jin Xu,Pei-Luan Li,and Yi-Cheng Pang,Commun.Theor.Phys.67(2017)137.

[20]L.Liu,F.Pan,and D.Xue,Opt.Inter.J.Light Electron Opt.125(2014)7020.

[21]J.Cao,C.Ma,H.Xie,and Z.Jiang,J.Comput.Nonlinear Dynam.4(2010)1003.

[22]R.Li,Opt.Int.J.Light Electron Opt.127(2016)6695.

[23]Z.Wang,X.Huang,and G.Shi,Comput.Math.Appl.62(2011)1531.

[24]Liping Chen,et al.,J.Comput.Nonlinear Dynam.10(2015).

[25]G.Velmurugan and R.Rakkiyappan,Nonlinear Dynam.11(2015)1.

[26]A.Babakhani,D.Baleanu,and R.Khanbabaie,Nonlinear Dynam.69(2012)721.

[27]M.Xiao,W.X.Zheng,and J.Cao,IEEE Trans.Neur.Net.Lear.Syst.24(2012)118.

[28]A.Y.T.Leung,H.X.Yang,and P.Zhu,Commun.Nonlinear Sci.19(2014)1142.

[29]Chengdai Huang,J.Cao,and Z.Ma,Inter.J.Syst.Sci.47(2015)1.

[30]Baleanu,Dumitru,et al.,Commun.Nonlinear Sci.25(2015)41.

[31]G.C.Wu and D.Baleanu,Nonlinear Dynam.80(2015)1697.

[32]W.Hu,D.Ding,Y.Zhang,N.Wang,and D.Liang,Optik 130(2017)189.

[33]S.K.Agrawal,M.Srivastava,and S.Das,Chaos,Solitons&Fractals 45(2012)628.

[34]H.Xi,S.Yu,R.Zhang,et al.,Opt.Inter.J.Light Electron Opt.125(2014)2036.

[35]S.Kuntanapreeda,Nonlinear Dynam.84(2016)2505.

[36]Kocamaz,Ugur Erkin,Y.Uyaroglu,and S.Vaidyanathan,Advances and Applications in Chaotic Systems,Springer International Publishing,Berlin(2016).

[37]A.Boulkroune,A.Bouzeriba,and T.Bouden,Neurocomputing 173(2016)606.

[38]Jun-Jun Liu,Xin Chen,and Jun-Min Wang,J.Dynam.Control Syst.22(2016)117.

[39]Bao-Zhu Guo,Hua-Cheng Zhou,et al.,J.Dynam.Control Syst.20(2014)539.

[40]B.Jiang,P.Shi,and Z.Mao,Circ.Syst.Signal Process.30(2011)1.

[41]Z.Gao,B.Jiang,P.Shi,et al.,J.Franklin Inst.349(2012)1543.

[42]L.Gao,Z.Wang,K.Zhou,et al.,Neurocomputing 166(2015)53.

[43]Dasgupta Tanmoy,P.Paral,and S.Bhattacharya,Int.Conference Comput.Commun.Inform.IEEE(2015)pp.1-6.

[44]S.Shao,M.Chen,and X.Yan,Nonlinear Dynam.83(2016)1855.

[45]M.Zak,Phys.Lett.A 133(1988)18.

[46]S.Mobayen,Nonlinear Dynam.82(2015)599.

[47]Di-Yi Chen,Yu-Xiao Liu,and Xiao-Yi Ma,Nonlinear Dynam.67(2011)893.

[48]Sundarapandian Vaidyanathan and Sivaperumal Sampath,Inter.J.Automat.Comput.9(2012)274.

[49]I.Podlubny,Math.Sci.Eng.(1999).

[50]W.Hu,D.Ding,and N.Wang,J.Comput.Nonlinear Dynam.12(2017)0410031.

[51]Dadras Sara and H.R.Momeni,Phys.A Stat.Mech.Appl.389(2010)2434.

[52]S.Bhalekar and V.Daftardar-Gejji,Fract.Calc.Appl.Anal.1(2011)1.