Fatima-Zahra Siyouri

Laboratoire de Physique Th`eorique,Departement de Physique Faculte des Sciences,Universite Mohammed V-Agdal Av.Ibn Battouta,B.P.1014,Agdal,Rabat,Morocco

1 Introduction

Over the last two decades,quantum correlations have been of renewed interest as the area of quantum information theory emerged and progressed.Entanglement,as a special type of quantum correlation,is an important resource in several applications of quantum information theory including quantum communications[1]and quantum cryptography.[2]Its quanti fication is considered as one of the most important topics in quantum information processing for both bipartite and multipartite systems.Despite the fact that the most of studies focus on quantifying two-qubit entangled states.Multipartite entanglement quanti fication has also attracted great attention recently.So,many efforts have been done in this direction by using various strategies.[3?10]In particular,Manet al.have presented a simple entanglement measure to quantify a multiqubit entangled state based on the idea of bipartitions.[3]Moreover,Adessoet al.have presented a geometric measure that is suitable for quantifying entanglement among any partitions of any multiple parties of a quantum system.[5]Furthermore,Suet al.have proposed a new way for quantifying entanglement of multipartite systems,which have a symmetrical structure and can be expressed as valence-bond-solid states.[6]

On the other hand,generally,all quantum systems can be described by using various tools,in particular,wavefunction,density matrix and Wigner function.However,the wave-function cannot describe all quantum states,except pure ones. And the density matrix is particularly suitable when a system is not completely controlled.For that fact,Eugene Wigner introduced the Wigner function[11]as a useful tool,especially in quantum optics,in order to account for quantum corrections to classical statistical mechanics.Its negativity is taken as a strong indicator of the non-classicality of quantum states.[12]Moreover,it has played an essential role with the rise of quantum information theory,principally due to the fact that it is considered as a resource in quantum computing and simulation.[13?14]Furthermore,because it has been proposed as an appropriate measure of quantumness.[15]

Recently,the investigation of quantum correlations by using the Wigner function has attracted substantial attention.[15?20]For instance,Banerjiet al.and Dahlet al.indicated that the negativity of Wigner function,which depicts non-classicality,can be used for detecting quantum entanglement.[14?15]In addition to that,lately we have used this negativity to detect and signal the presence of general quantum correlations in continuous variable bipartite mixed states[20]and we have shown that the Wigner function is not sensitive to all kinds of quantum correlations but it only witnesses entanglement.In this paper,we extend our work to the case of multi-qubit GHZ-entangled squeezed states.However,we focus our attention only on the study of the special kind of quantum correlations that is quantum entanglement.So in this respect,we work with the tripartite negativity as a measure of entanglement presents in the mixed tripartite GHZ-entangled squeezed states.Our goal is not only to con firm previous results,[15?16,20]Wigner function does detect quantum entanglement,but also to generalize the study of the role of Wigner function in detecting and quantifying quantum entanglement.This is done by answering the question:whether Wigner function detect and quantify entanglement for only bipartite systems or also multipartite ones?

In this paper,we investigate the relevancy of the Wigner function in capturing and quantifying multipar-tite quantum correlations in a given quantum system.In Sec.2,we study the behavior of entanglement that is present in GHZ states made of tripartite squeezed states by calculating tripartite negativity.In Sec.3,we de fine the Wigner function for our system.Then,in Sec.4,we analyze the behavior of the Wigner function and compare it to the behavior of the quantum correlations.A discussion and overview of our results are then presented as a conclusion.

2 Quantum Correlations for Tripartite GHZSqueezed States

2.1 Squeezed States and the GHZ-Werner-Type States

In order to generalize the study that was done in Ref.[20],one employs the GHZ-Werner-type states made of tripartite squeezed states,which are characterized by the fact that the indetermination in one of the two quadrature-components of the electromagnetic field is smaller than in the usual coherent states.[21]Interestingly,GHZ-Werner-type states are formed by a mixtures of a GHZ-type state and the completely unpolarized state.

The Fock state expansion of the single-mode squeezed state,[21]is given by:

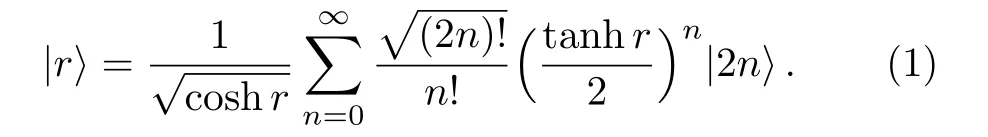
Let us consider an arbitrary tripartite GHZ-squeezed states having the same parameter|r|2. Consider that|?r〉isπradians out of phase with the corresponding squeezed states.Then,the wave function of tripartite GHZ-squeezed states will take the following form:

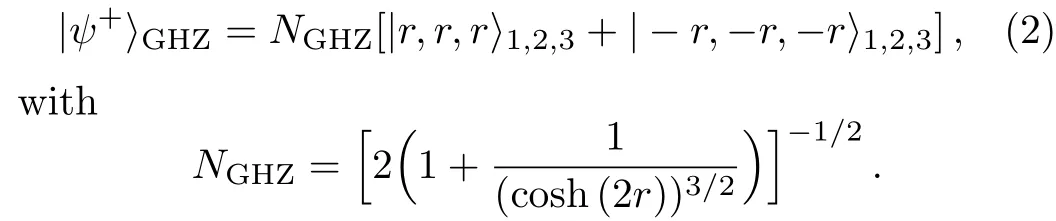
The even and the odd squeezed states|±〉are de fined by

Therefore,the GHZ-Werner-type state that we intend to use in our investigation,

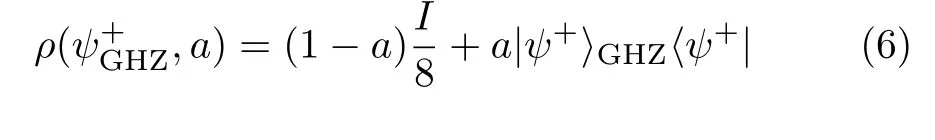
It is worthwhile to notice that the density matrix here is represented in the follwing basis:{|+++〉,|++?〉,|+?+〉,|+??〉,|?++〉,|?+?〉,|??+〉,|???〉}.

2.2 Entanglement

The negativity(N)is an entanglement measure,which is derived from the positive partial transpose(PPT)criterion for separability.It is de fined as,[22]

where,ρTCis the partial transpose ofρwith respect to the subsystemC,andλi(ρTC)are the eigenvalues ofρTC.One can interpret the negativity equivalently as the sum of the absolute values of the negative eigenvalues ofρTC,[22]and it depends on the subsystem on which we perform the partial transpose ofρ.

When negativity is higher than zero(N＞0),we deduce that there is an entanglement between the subsystemCand the subsystemAB,but,inversely if there is entanglement between the subsystemsCandAB,the negativity is not necessarily higher than zero.Therefore,tripartite negativity can be de fined,[23]

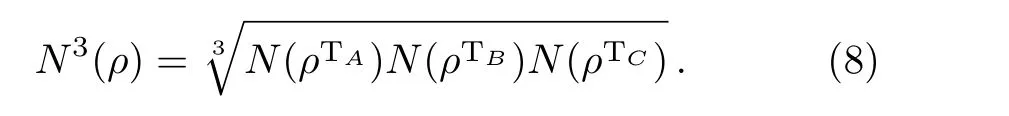
This quanti fier will be different from zero only when the entanglement is shared between all of the three subsystems(it is a complete tripartite entanglement).[23]

3 Wigner Function of the Tripartite GHZType Squeezed States

Wigner function is regarded as a powerful indicator of the non-classicality of single mode states.[21,24?25]Here,we will show that it does apply also for multipartite systems by investigating its behavior in the case of the tripartite Greenberger–Horne–Zeilinger(GHZ)-type squeezed states.

For a quantum system described by the density matrixρ,the Wigner function is de fined by[21]

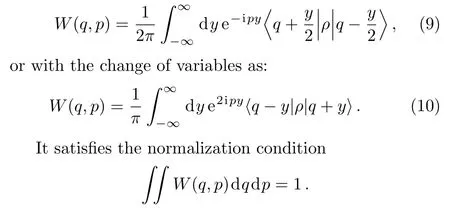
From which the non-classical volume is de fined as a doubled volume of the integrated negative part of the Wigner function that may be expressed as[15]

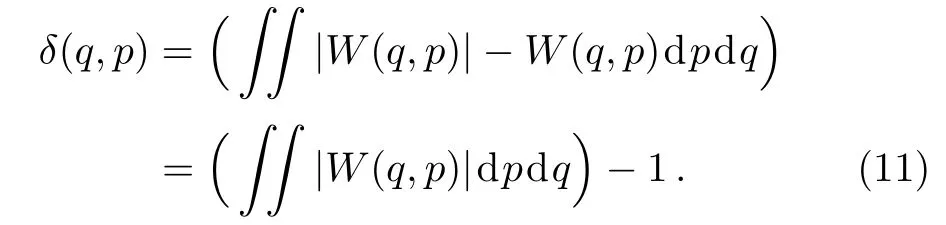
This quantity(δ(q,p))is by de finition equal to zero whenever Wigner function is non-negative.In this work we consider the volume of the negative part of the Wigner function as a parameter of non-classicality(δ(q,p)),which can be used consequently to detect and quantify the entanglement between the three modes of the tripartite system.

The generalization of Wigner function to a three mode state is expressed as:[26?27]

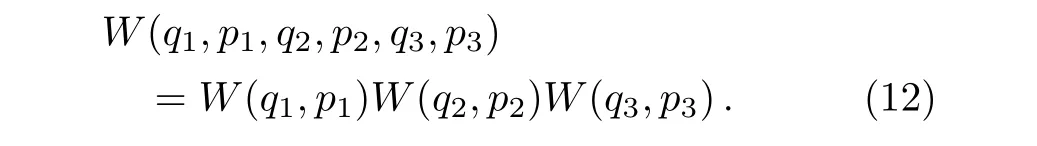
For a single mode squeezed state,with squeezing parameterr,the Wigner function is given by[28]

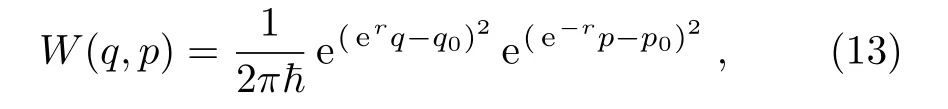
whereqandpare position and momentum respectively.

The Wigner function of a three mode squeezed state is a function of the six quadrature variablesq1,p1,q2,p2,q3,andp3,[15]it can be written as

and the interference structure,which appears between the three peaks is given by

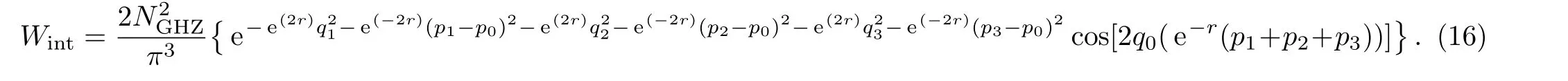
Therefore,the Wigner function of mixed tripartite squeezed states of GHZ type,ρ(ψ+GHZ,a),is

with 1/π3is the Wigner function of identity.

4 Behaviors of Quantum Entanglement and Wigner Function

In order to explore the behavior of entanglement present in the tripartite GHZ-type squeezed states,we plot in Fig.1 its variation as function of the mixing parameteraand the squeezing parameterr.

From Fig.1,we see that the quantum entanglement(tripartite negativity)for the states increases with increasing values of the mixing parameteraand the squeezing parameterr.Furthermore,it is absent for small values ofaandrand it attains its maximum value for the larger values of these parameters.So one can affirm,for instance,that the pure tripartite states(a=1)contain more quantum correlations than the corresponding mixed ones(0≤a＜1).

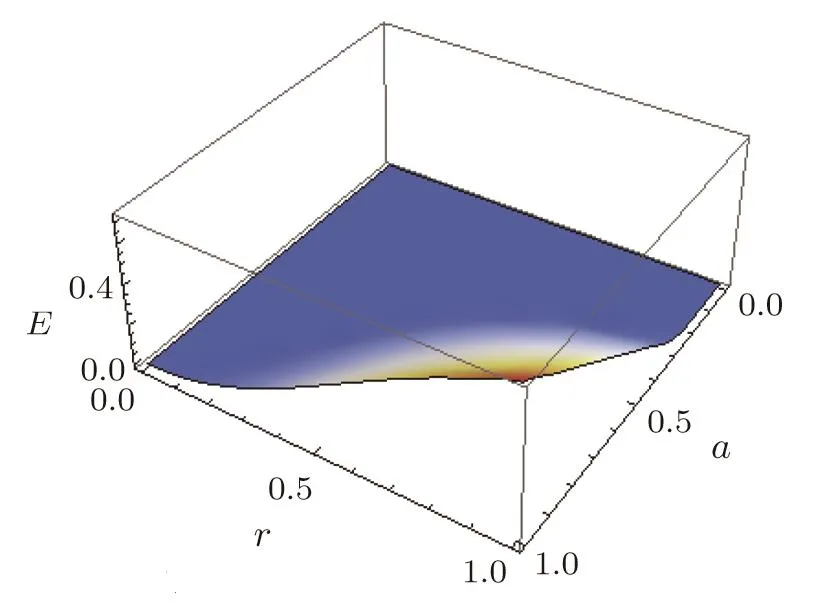
Fig.1 Entanglement plotted with respect to mixing parameter a and squeezing parameter r.

On the other hand,to shed some light on the structure and the behavior of Wigner function for multipartite system we have chosen to show in Fig.2 their plots as a function ofq1,p2,andp3as these are more suitable to study the correlations between the three modes.The fact that,it is negative in certain regions is indicative of the non-classicality of the corresponding states that in turn indicates the presence of non-classical correlations between the three modes of the tripartite system.

In Fig.2 one can see that the volume of the negative parts of the Wigner function increases with the mixing parameter,the squeezing parameterrand the separation distanceq0(Figs.2(b),2(c),2(d),and 2(f)).It is seen also that the number of fringes as well as the volume of the fringes change with changing the squeezing parameterr(Figs.2(b)and 2(c)).Moreover,Fig.2(a)shows that forq0=0,the structure of the Wigner function for the tripartite GHZ-type squeezed states reduces to the structure of a single squeezed vacuum state,but it is displaced in the phase space.Furthermore,Fig.2(e)shows that the volume of the negative part of Wigner function increases with increasing the mean value of positionq0and decreasing the mean value of momentump0.

Now,we turn our attention to verify if the multipartite quantum correlations can also be detected by the Wigner function.For that purpose,we displayed in Fig.3 2D behavior of the Wigner function and that of the quantum entanglement as a function of the squeezing parameterr.

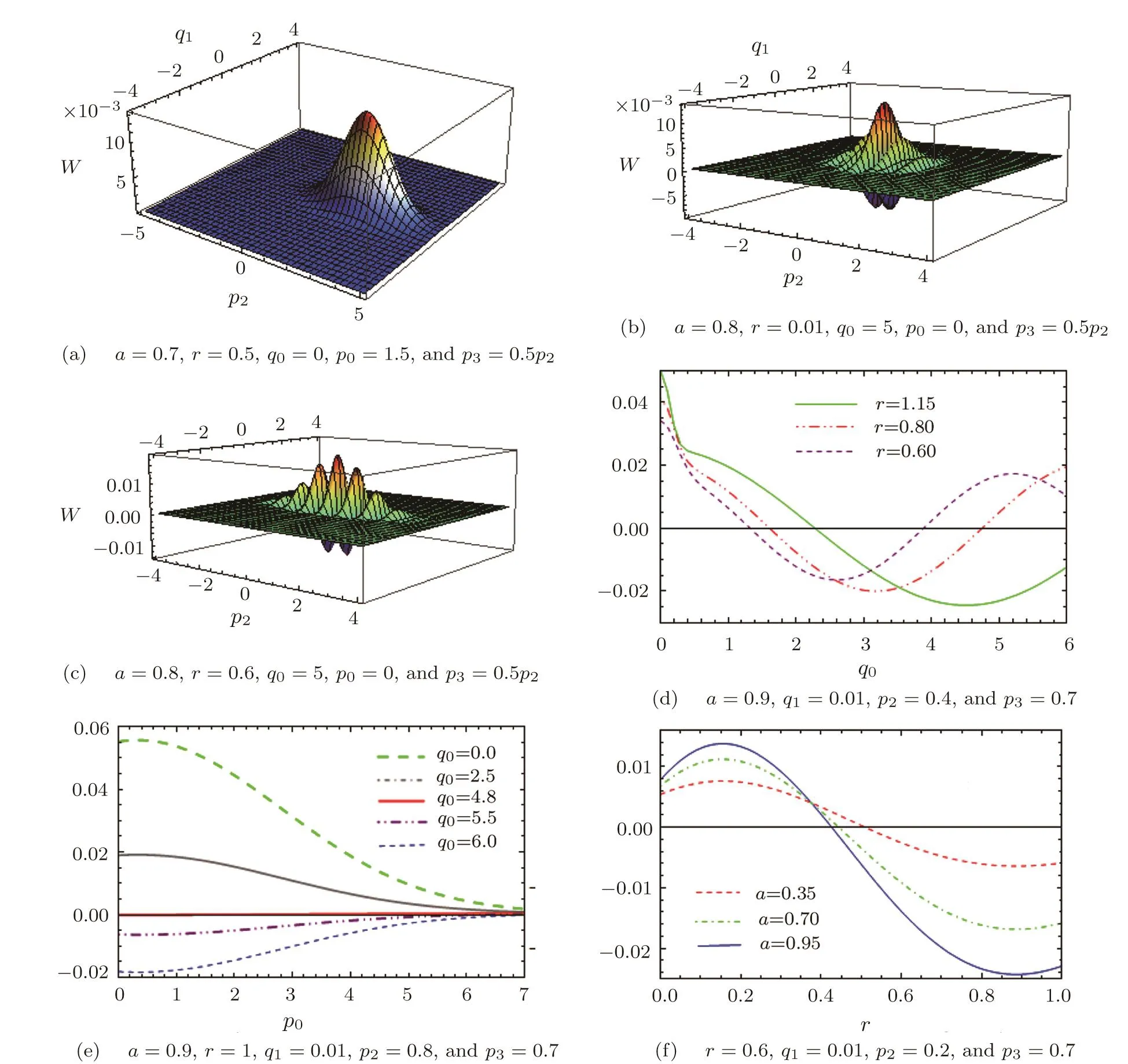
Fig.2 Wigner function W(q1,p2,p3)plotted as function of{q1,p2,p3=0.5p2}(a),(b),(c),q0(d),p0(e)and r(f).

The Plots in Fig.3,show that whenever the Wigner function is negative there is entanglement and the opposite is also true,whenever there is entanglement the Wigner function is negative i.e.the existence of entanglement allows to have a negative Wigner function.Furthermore,one can see that increasing entanglement present in the tripartite states by increasing the parametersaorrincreases the overall volume of the negative region in the plot of the Wigner function.In view of this,one can conclude that the Wigner function is not sensitive to only bipartite quantum correlations[20]but also toamultipartite ones.

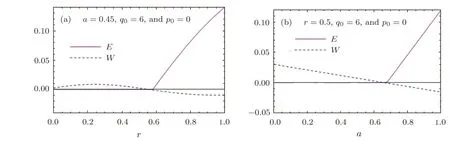
Fig.3 Entanglement and Wigner function for the GHZ state for fixed values of p1,q2,and q3(p1=q2=q3=0)with respect to squeezed parameter r(a)and mixing parameter a(b).

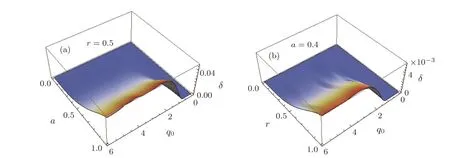
Fig.4 Variation of the non-classicality parameter δ(q1,p2,p3)for the GHZ state.

In Fig.4,we show the variation of non-classicality parameterδ(q1,p2,p3)as function of the squeezing parameterrand the mixing parametera.

It is seen in Fig.4 that the indicator of the nonclassicalityδ(q1,p2,p3)showed similar variation with the order of the mixing parameteraand squeezing parameterras entanglement.In the sens that,increasing values ofrandaenhance this indicator as the volume of negative part also increases;this causes the emergence of the interference pattern,which in turn re flects the presence of entanglement.Fora=1(pure states)the volume occupied by the indicator of the non-classicalityδattain it’s maximum value.Moreover,for small values of parametersaandr,the non classicality parameterδis absent correspondingly leading to the absence of entanglement between the three modes of the tripartite system.Indeed,the parameterδshould be also considered as a strong tool to quantify the amount of quantum correlations present in the tripartite states.

5 Conclusion

In this letter,we have investigated the role of Wigner function in capturing and quantifying multipartite quantum entanglement.In this respect,we have shown that the existence of entanglement in tripartite system guarantees the negativity of the Wigner function and the reciprocal is also true.Therefore,we have found that the volume of this negativity may be used as a measure of entanglement even for tripartite system.So,we can conclude that this work can be regarded as a generalization of the role of Wigner function in capturing bipartite entanglement in bipartite systems to a multipartite systems.Furthermore,we deem that it does represent a major step forward in understanding its quanti fication in a such systems.

[1]C.H.Bennett,G.Brassard,C.Crpeau,et al.,Phys.Rev.Lett.70(1993)1895.

[2]A.K.Ekert,Phys.Rev.Lett.67(1991)661.

[3]Z.X.Man,Y.J.Xia,and N.B.An,New J.Phys.12(2010)033020.

[4]Z.X.Man,Y.J.Xia,and S.M.Fei,J.Phys.A:Math.Theor.45(2012)195306.

[5]G.Adesso,A.Sera fini,and F.Illuminati,Phys.Rev.Lett.93(2004)220504.

[6]P.Y.Su,W.D.Li,X.P.Ma,et al.,Quantum Inf.Proc.16(2017)190.

[7]L.Aolita,R.Chaves,D.Cavalcanti,et al.,Phys.Rev.Lett.100(2008)080501.

[8]M.Hein,W.D¨ur,and H.J.Briegel,Phys.Rev.A 71(2005)032350.

[9]Z.X.Man,Y.J.Xia,and N.B.An,Phys.Rev.A 78(2008)064301.

[10]N.B.An and J.Kim,Phys.Rev.A 79(2009)022303.

[11]E.P.Wigner,Phys.Rev.40(1932)749.

[12]N.L¨utkenhaus and S.M.Barnett,Phys.Rev.A 51(1995)3340.

[13]A.Mari and J.Eisert,Phys.Rev.Lett.109(2012)230503.

[14]V.Veitch,N.Wiebe,C.Ferrie,and J.Emerson,New J.Phys.15(2013)013037.

[15]A.Kenfack and K.Zyczkowski,J.Opt.B:Quantum Semiclass Opt.6(2004)396.

[16]A.Banerji,R.P.Singh,and A.Bandyopadhyay,Opt.Commun.330(2014)85.

[17]J.P.Dahl,H.Mack,A.Wolf,and W.P.Schleich,Phys.Rev.A 74(2006)042323.

[18]R.Simon,Phys.Rev.Lett.84(2000)2726.

[19]R.Taghiabadi,S.J.Akhtarshenas,and M.Sarbishaei,Quantum Inf.Proc.15(2016)1999.

[20]F.Siyouri,M.El Baz,and Y.Hassouni,Int.J.Mod.Phys.B 30(2016)1650187.

[21]C.Gerry and P.Knight,Introductory Quantum Optics,Cambridge University Press,New York(2005).

[22]G.Vidal and R.F.Werner,Phys.Rev.A 65(2002)032314.

[23]C.Sabin and G.Garca-Alcaine,Eur.Phys.J.D 48(2008)435.

[24]V.V.Dodonov,J.Opt.B:Quantum Semiclass.Opt.4(2002)R1.

[25]A.Barenco,D.Deutsch,A.Ekert,and R.Jozsa,Phys.Rev.Lett.74(1995)4083.

[26]He-Jun Wu and Hong-Yi Fan,Mod.Phys.Lett.B 11(1997)544.

[27]Nian-Quan Jiang,J.Opt.B:Quantum Semiclass Opt.7(2005)264.

[28]U.Leonhardt,Measuring the Quantum State of Light,Cambridge University Press,Cambridge(1997).