A New Negative Discrete Hierarchy and Its N-Fold Darboux Transformation?
Ning Zhang(張寧) and Tie-Cheng Xia(夏鐵成)
1Department of Basical Courses,Shandong University of Science and Technology,Taian 271019,China
2Department of Mathematics,Shanghai University,Shanghai 200444,China
1 Introduction
Itis an importanttask in soliton theory to find integrable lattice system such as those connecting with well-known physical meaning equations. In past decades,lots of nonlinear integrable lattice soliton systems have been obtained and discussed successfully,e.g. the Ablowitz–Ladik lattice,[1]the Toda lattice,[2]the differential-difference KdV equation,[3]the Blaszakl–Marciniak lattice,[4?5]and so on.[6?10]It is well known,there are many systematic approaches to obtain explicit solutions of lattice soliton systems,such as the inverse scattering transformation,[11]the Hirota technique,[12]the algebra-geometric method,[13]the Darboux transformation,[14?15]etc.Among them,it has been proved that Darboux transformation is one of the most fruitful algorithmic procedures to get explicit solutions of nonlinear partial differential equations from a trivial seed.[16?22]
In this paper,we consider a discrete spectral problem

whereqn=q(n,t),pn=p(n,t)are potentials,andλis the spectral parameter andλt=0.For a lattice functionfn=f(n),the shift operatorE,the inverse ofEand difference operatorDare de fined as follows

If letpn→qn/λ,qn→λpn,then the spctral problem(1)can be changed into the spectral problem

which was considered by Dinget al.,where only a positive discrete hierarchy and 1-fold Darboux transformation were obtained.[23]So in this paper,we would like to further consider a negative discrete hierarchy and its properties associated with spectral problem(1).
The organization of this paper is as follows.In Sec.2,we first establish a negative discrete hierarchy related to the spectral problem(1).In Sec.3,it is shown that the hierarchy is integrable in Liouville sense and possesses bi-Hamiltonian structure.In Sec.4,anN-fold Darboux transformation for negative discrete hierarchy is established with the help of gauge transformations of Lax pair.As an application,some exact solutions for a discrete equation in the negative hierarchy are given in Sec.5.
2 A New Negative Discrete Hierarchy
In order to get the discrete integrable system,we first proceed to solve the stationary discrete zero curvature equation

From Eq.(5),it is easy to obtain the following recursion relations


then compatibility condition between Eqs.(1)and(12)gives zero curvature equation
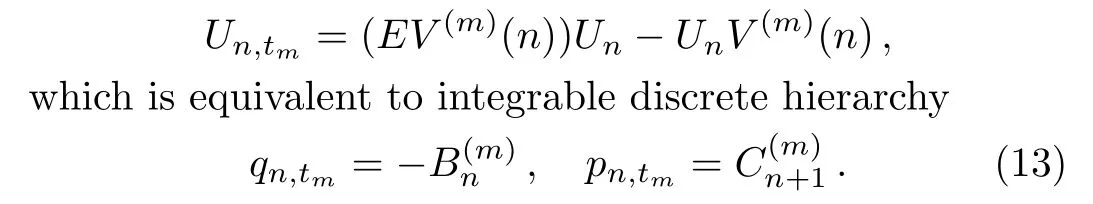
We can give the first two discrete integrable systems in the hierarchy:
Whenm=0,the hierarchy(13)gives
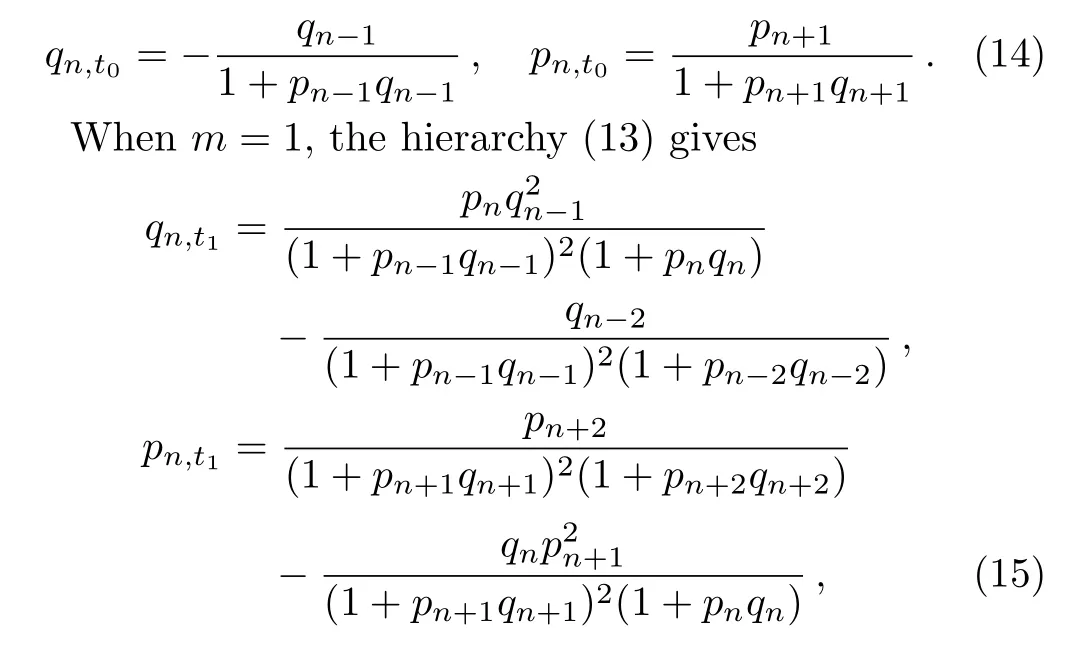
Eq.(14)is a new negative discrete system,whose time part of the Lax pairs is
V(n)=V(0)(n)
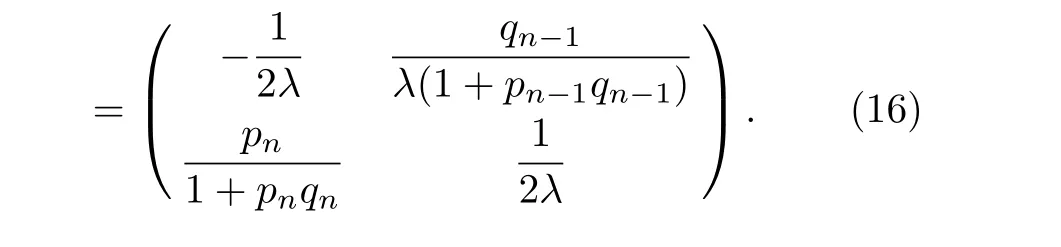
3 Bi-Hamiltonian Structures of the Hierarchy
De fine
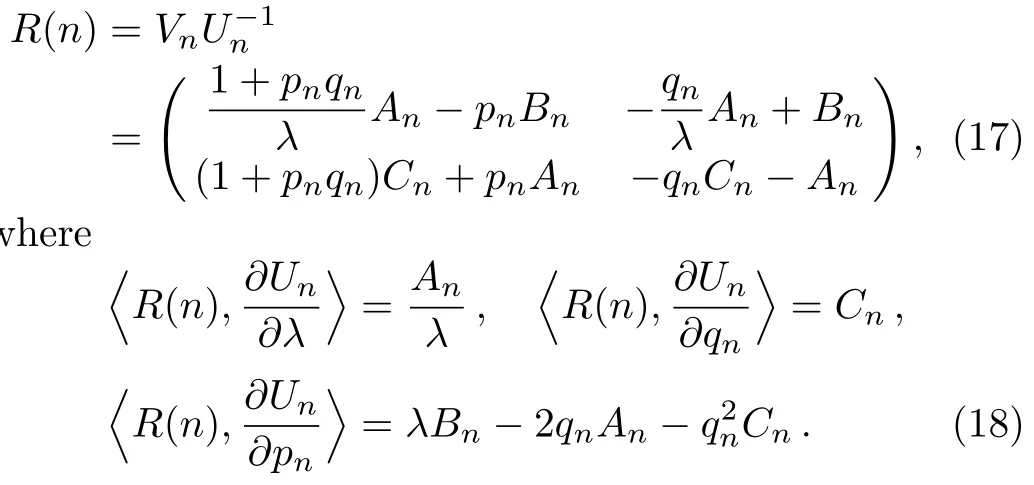
By implying the discrete trace identity

withεto be determined later.Substituting expressions

into Eq.(20)and comparing the coefficient ofλm?1,we obtain
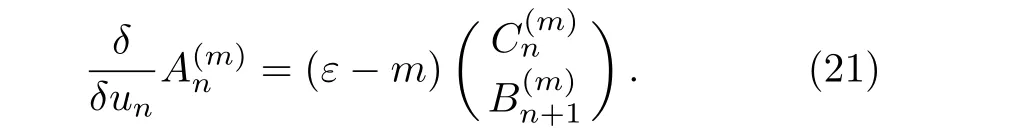
Takingm=1 in Eq.(21),a direct calculation shows thatε=0,so we get
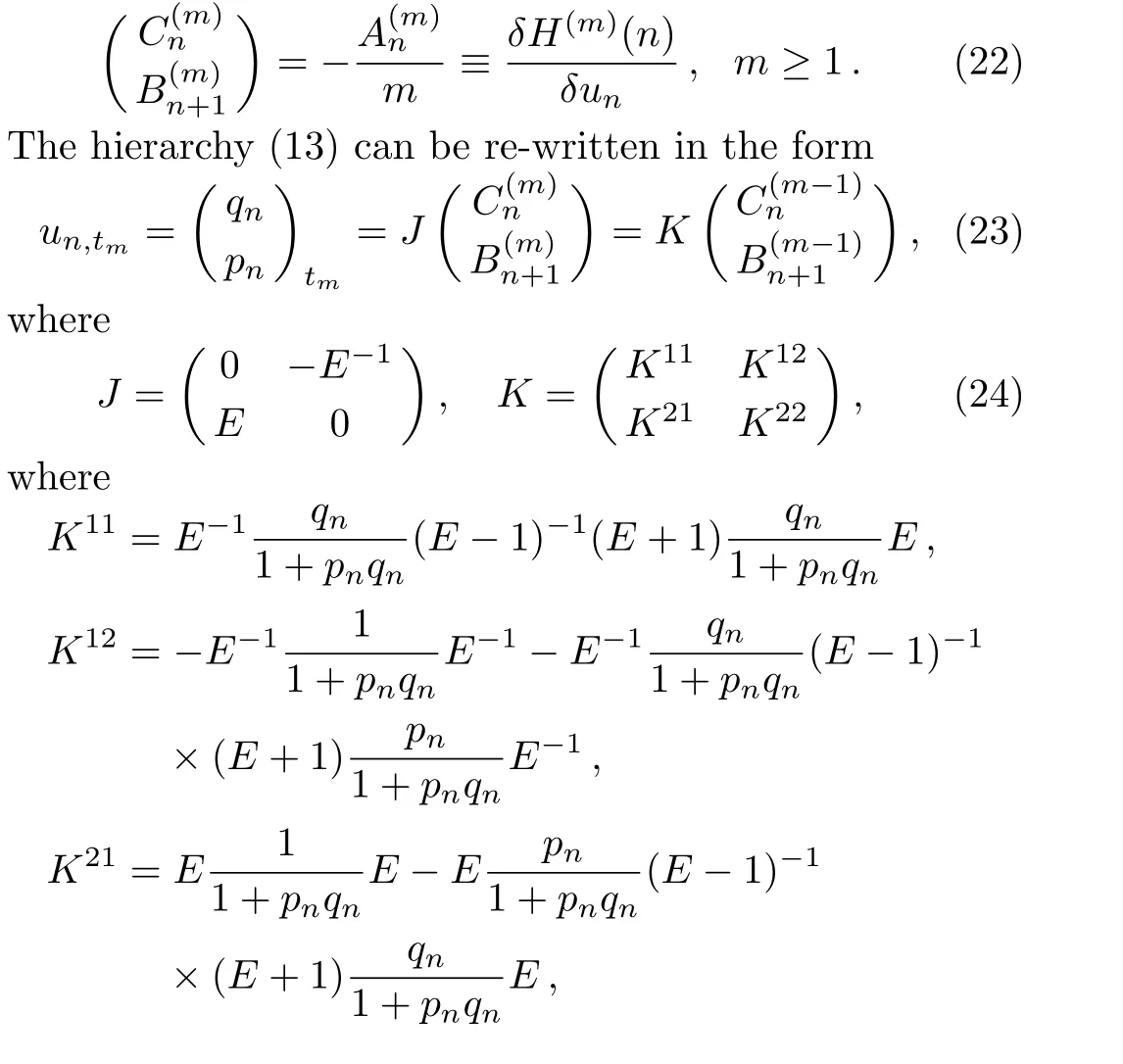

It is easy to verify thatJandKare all skew-symmetric operators,i.e.J=?J?,K=?K?.Then substituting Eq.(22)into Eq.(23)gives the bi-Hamitonian structure for the hierarchy(13)

We can further prove the following theorem:

4N-Fold Darboux Transformation
As an illustrative example,we construct theN-fold Darboux transformation for the system(14)based on its Lax pair

In fact,the Darboux transformation of the system(14)is a special gauge transformation of Lax pair(26)and(27).Consider the following gauge transformation

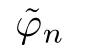
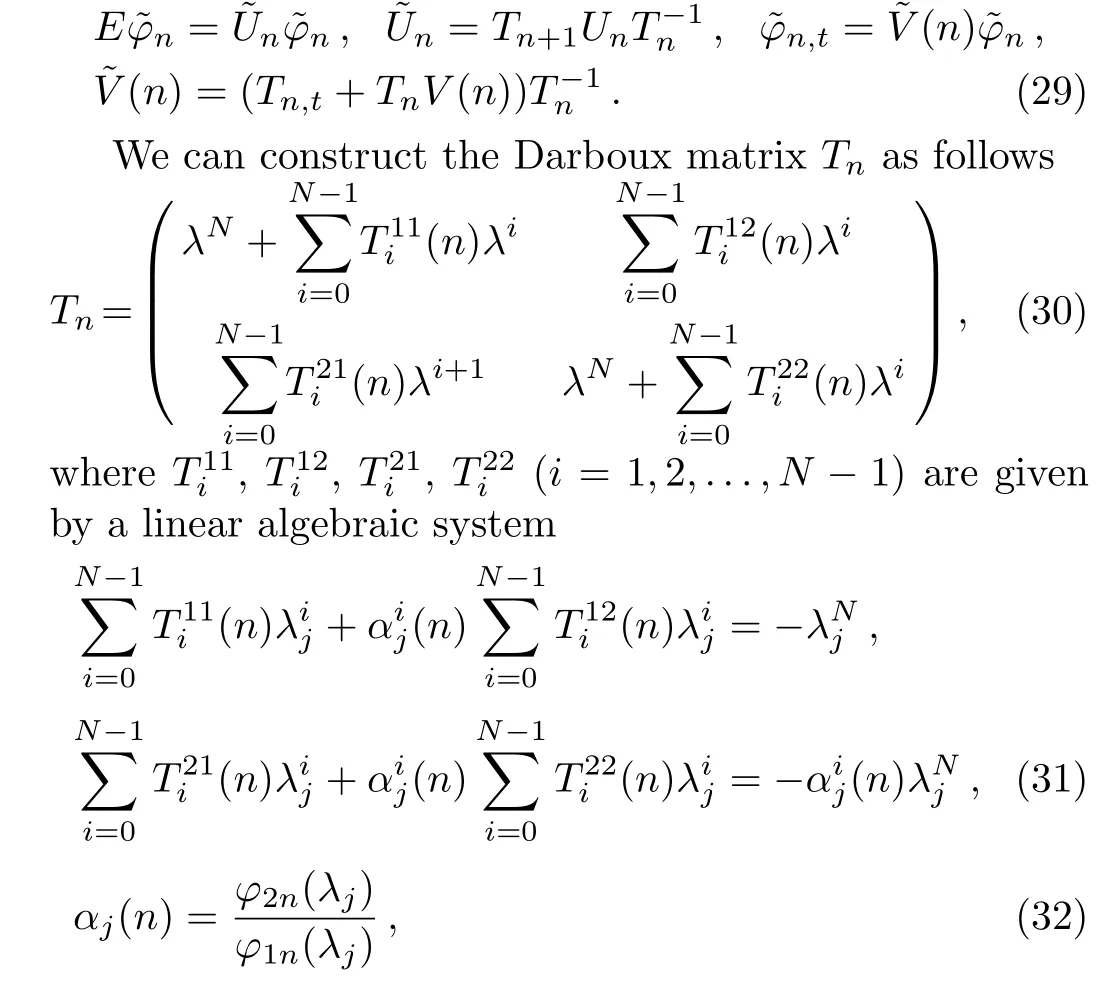
whereφin=(φi1n(λj),φi2n(λj))T(i=1,2)are two basic solutions of Lax pair(26)and(27),andλj(j=1,2,...,2N)are 2Nparameters suitably chosen so that the determinant of the coefficients of the system(31)is nonzero.According to Eqs.(30)–(32),we can show that detTnis a(2N)-th order polynomial ofλ

By using above fact,we can prove the following proposition.

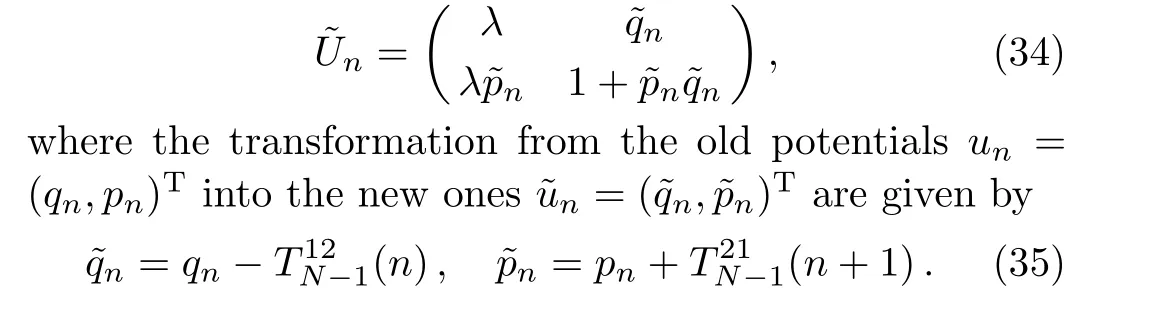
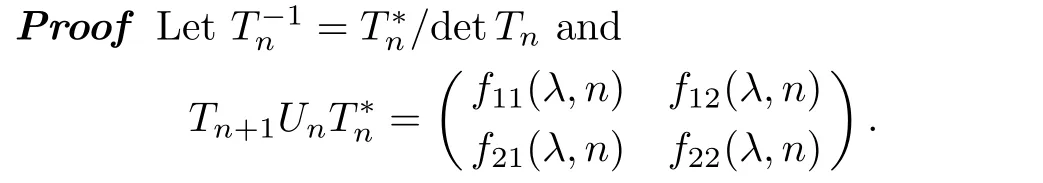
It is easy to see thatf11(λ,n)andf22(λ,n)are(2N+1)-th order polynomials inλ,f12(λ,n),andf21(λ,n)are(2N)-th order polynomials inλ,respectively.From Eqs.(26)and(32),we can get
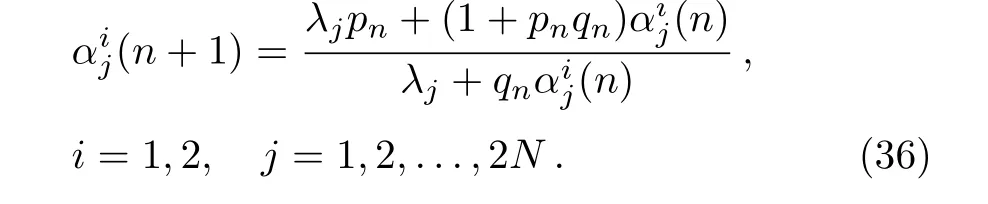
Moreover,by virtue of Eqs.(33)and(36),it can be proved thatλj(j= 1,2,...,2N)are roots offk,l(λ,n)(k,l=1,2),which together with Eq.(33)imply thatfk,l(λ,n)(k,l=1,2)may be divided by detTn.Therefore,we have
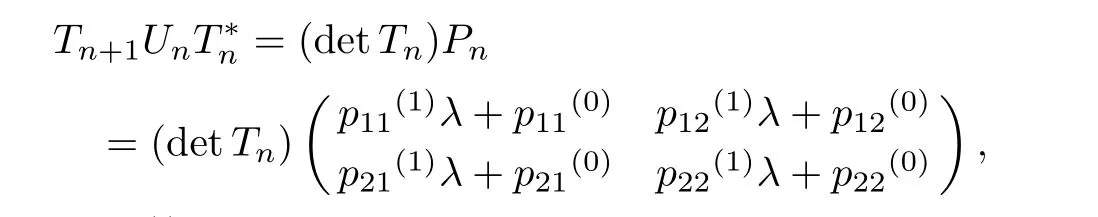

By comparing the coefficients ofλN+1,λNin Eq.(37),we obtain


Proposition 2Under the Darboux transformation(28),the matrix?V(n)de fined by Eq.(29)has the same form as

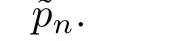
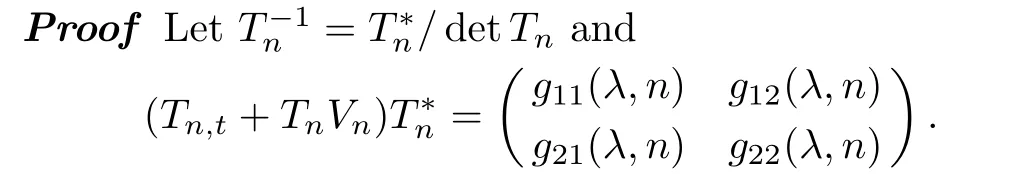
It is obvious thatg11(λ,n),g22(λ,n)org12(λ,n),g21(λ,n)are(2N+1)-th or(2N)-th polynomials inλ,respectively.It can be checked thatλj(j=1,2,...,2N)are roots ofgk,l(λ,n)(k,l=1,2). Therefore,the matrix(Tn,t+TnVn)T?nis written as
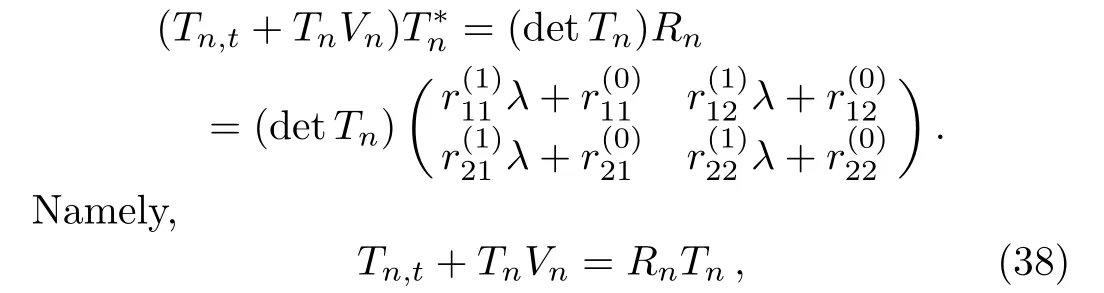
whererl ij(i,j=1,2;l=0,1)are independent ofλ.Comparing the coefficients ofλi(i=N+1,N,N?1)in Eq.(38),we obtain


which leads to the relations(35)between old potential functions(pn,qn)and new potential functions(?pn,?qn).
By using above facts,we can obtain the following theorem:
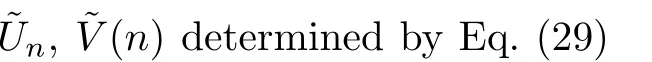
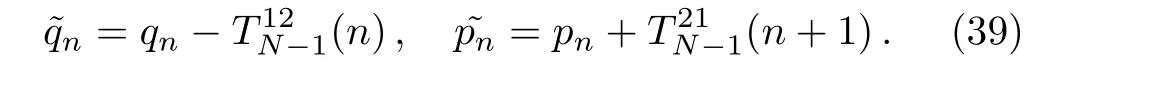
5 The Exact Solutions
In this section,we will give some exact solutions of system(14)via Darboux transformation(39).Taking the trivial solutionqn=0,pn=0,we obtain two kinds of exact solutions of the Lax pair(26)and(27)withλ=λj(j=1,2,...,2N)as follow

According to Eqs.(32)and(36),we have

By use of Cramer’s rule,the linear algebraic system(41)leads to
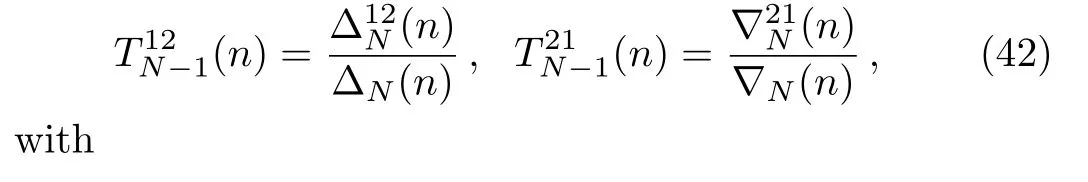
Next,we give some exact solutions of the system(14)via Darboux transformation(39)for two cases whenN=1 andN=2 respectively.
Case 1WhenN=1,formula(42)leads to


Therefore,by using the Darboux transformation(39),we obtain new solutions of the system(14)as follows
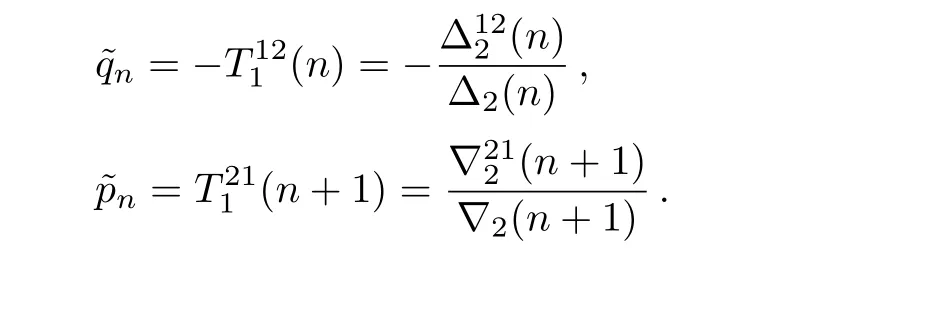
[1]M.J.Ablowitz and J.F.Ladik,J.Math.Phys.16(1975)598.
[2]Gui-Zhang Tu,J.Phys.A:Math.Gen.23(1990)3903.
[3]K.M.Tamizhmani an M.Lakshmana,J.Phys.A:Math.Gen.16(1983)3773.
[4]M.Blaszak and K.Marciniak,J.Math.Phys.35(1994)4661.
[5]Fa-Jun Yu and Li Li,J.Modern Phys.B 25(2011)3371.
[6]Xin-Yue Li,Qiu-lan Zhao,Yu-Xia Li,and Huan-He Dong,J.Nonl.Sci.Appl.8(2015)496.
[7]Xiang-Rong Wang,Xiao-En Zhang,and Pei-Yi Zhao,Abst.Appl.Anal.ID253102(2014)1.
[8]Xi-Xiang Xu,Appl.Math.Comput.216(1)(2010)344.
[9]Ning Zhang and Huan-He Dong,Modern Phys.Lett.B 23(2009)3491.
[10]Ning Zhang and Tie-Cheng Xia,Int.J.Nonl.Sci.Num.Simulat.16(2015)301.
[11]M.J.Ablowitz and H.Segur,Solitons and the Inverse Scattering Transform,SIAM,Philadelphia(1981).
[12]Hirota Ryogo and Satsuma Junkichi,Progr.Theoret.Phys.Suppl.59(1976)64.
[13]Yu-Qing Li,Huan-He Dong,and Bao-Shu Yin,J.Appl.Math.ID416472(2014)1.
[14]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer-Verlag,Berlin(1991).
[15]Chao-Hao Gu,He-Sheng Hu,and Zi-Xiang Zhou,Darboux Transformation in Soliton Theory and Its Geometric Applications,Shanghai Scienti fic and Technical Publishers,Shanghai(1999).
[16]Yong Zhang,Huan-He Dong,Xiao-En Zhang,and Hong-Wei Yang,Comput.Math.Appl.73(2017)246.
[17]Yu-Feng Zhang,Hong-Qing Zhang,and Xin-Bo Gong,Gongcheng Shuxue Xuebao 18(2001)93(in Chinese).
[18]Wen-Xiu Ma and Xian-Guo Geng,Centrc de Recherches Mathematiques CMR Proceedings and Lecture Notes 29(2001)313.
[19]En-Gui Fan,J.Phys.A 38(2005)1063.
[20]Sen-Yue Lou,Man Jia,Xiao-Yan Tang,and Fei Huang,Phys.Rev.E 75(2007)056318.
[21]En-Gui Fan,Commun.Theor.Phys.37(2002)145.
[22]Sen-Yue Lou,Man Jia,Fei Huang,and Xiao-Yan Tang,Int.J.Theor.Phys.46(2007)2082.
[23]Hai-Yong Ding,Xi-Xiang Xu,and Xiang-Dong Zhao,Chin.Phys.13(2004)0125.
[24]Huan-He Dong,Yong Zhang,and Xiao-En Zhang,Commun.Nonl.Sci.Numer.Simulat.36(2016)354.
 Communications in Theoretical Physics2017年12期
Communications in Theoretical Physics2017年12期
- Communications in Theoretical Physics的其它文章
- Rumor Spreading Model with Immunization Strategy and Delay Time on Homogeneous Networks?
- In fluence of Cell-Cell Interactions on the Population Growth Rate in a Tumor?
- Linear Analysis of Obliquely Propagating Longitudinal Waves in Partially Spin Polarized Degenerate Magnetized Plasma
- Damped Kadomtsev–Petviashvili Equation for Weakly Dissipative Solitons in Dense Relativistic Degenerate Plasmas
- General Solutions for Hydromagnetic Free Convection Flow over an In finite Plate with Newtonian Heating,Mass Diffusion and Chemical Reaction
- New Exact Traveling Wave Solutions of the Unstable Nonlinear Schrodinger Equations
