李余輝

(桂林電子科技大學(xué)數(shù)學(xué)與計(jì)算科學(xué)學(xué)院,廣西桂林541004)

李余輝

(桂林電子科技大學(xué)數(shù)學(xué)與計(jì)算科學(xué)學(xué)院,廣西桂林541004)

本文研究了Brown運(yùn)動(dòng)在Hlder范數(shù)與容度下的泛函極限問(wèn)題.利用大偏差小偏差方法,獲得了Brown運(yùn)動(dòng)增量局部泛函極限的收斂速度,推廣了文[4]中的結(jié)果.

Brown運(yùn)動(dòng);收斂速度;Hlder范數(shù);容度

1　引言

考慮經(jīng)典的Wiener空間(B,H,μ),設(shè)Dr,p是Wiener泛函的Sobolev空間,即

其中Lp記為(B,μ)上的實(shí)值函數(shù)的Lp空間,L是(B,H,μ)上的Ornstein-Uhlenbeck算子.對(duì)r≥0,p＞1,(r,p)-容度定義如下

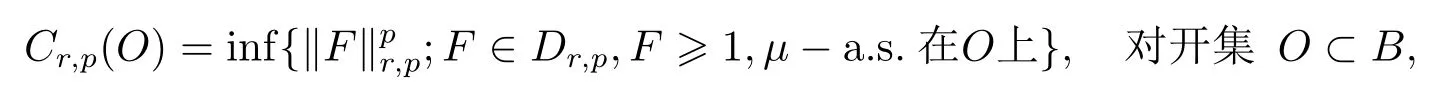
且對(duì)任意集合A?B有,Cr,p(A)=inf{Cr,p(O);A?O?B,O是開(kāi)集}.設(shè)Cd為從[0,1]到Rd的連續(xù)函數(shù)空間,賦予上確界范數(shù)‖f‖=|f(t)|.記={f∈Cd;f(0)=0}, Hd={f∈;f(t)=|(t)|2dt＜∞},Hd是一定義如下內(nèi)積的Hilbert空間,〈r1,r2〉Hd= (1(s),2(s))ds.設(shè)μ是上的Wiener測(cè)度,(,Hd,μ)是一經(jīng)典Wiener空間.下面考慮如下兩個(gè)Banach空間

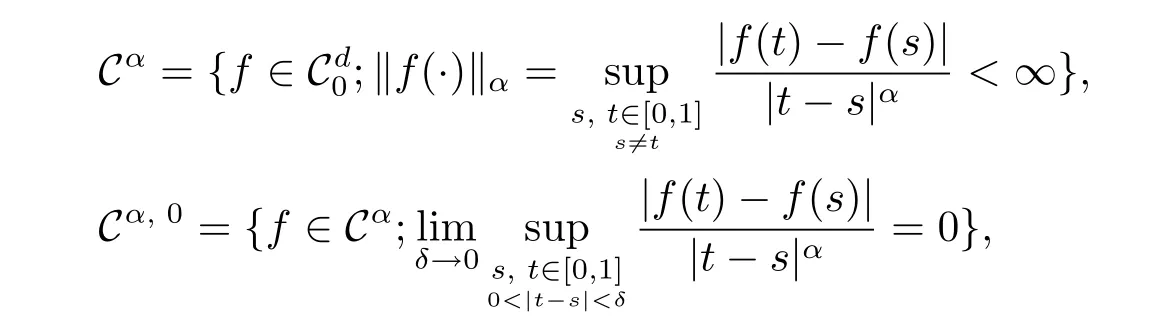
自從Yoshida[1]首先得到了關(guān)于容度Cr,p意義的大偏差結(jié)論,近年來(lái)關(guān)于Brown運(yùn)動(dòng)在Hlder范數(shù)下的擬必然泛函極限理論開(kāi)始受到關(guān)注.Baldi與Roynette[2]利用大偏差得到了Brown運(yùn)動(dòng)在Hlder范數(shù)下的收斂速度,并證明了存在k=k(α)≥0,使得

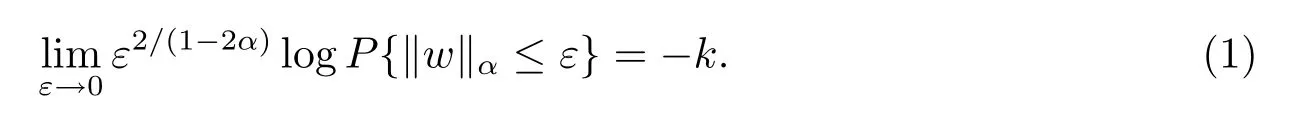
進(jìn)一步,對(duì)任意f∈K與γ=(1-2α)/2有

后來(lái),Chen與Balakrishnan[3]得到Brown運(yùn)動(dòng)在Hlder范數(shù)與容度Cr,p意義下泛函重對(duì)數(shù)律的極限定理.本文利用Hlder范數(shù)下的大偏差小偏差,得到了Brown運(yùn)動(dòng)增量在Hlder范數(shù)下,關(guān)于容度Cr,p意義下局部泛函極限的收斂速度.主要結(jié)果如下.

定理1設(shè)ru定義為從R+到R+的單調(diào)不減函數(shù),滿足0＜ru≤u且u/ru單調(diào)不減.記σu=,若=∞,則在Cr,p-q.s.意義下有

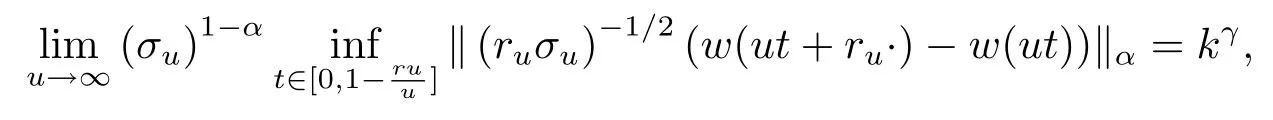
其中γ=(1-2α)/2,k＞0如式(1)中所定義.

定理1的證明可由引理5與引理6得到,在此之前敘述已有的相關(guān)結(jié)果.

2　定理1的證明

引理1(見(jiàn)文獻(xiàn)[3]定理2.1)設(shè){Sε}ε＞0是Cα,0上一雙射線性算子,使得對(duì)任意ε＞0及A?Cα,0有=μ(ε-1/2A),則對(duì)(r,p)∈[0,∞)×(1,∞),有

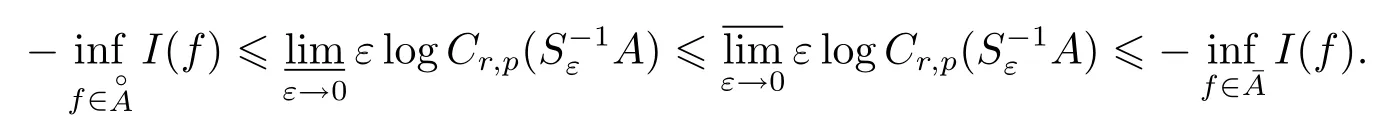
引理2(見(jiàn)文獻(xiàn)[6]引理2.1)設(shè)k∈N,q1,q2∈(1,∞)滿足1/p=1/q1+1/q2,則存在常數(shù)c=c(k,p,q1,q2)＞0使得對(duì)任意-∞＜ai＜bi＜∞,δ∈(0,1),及Fi∈Dk,kq1有下式成立

引理3設(shè)k,p,q1,q2如引理2中定義.對(duì)任意ε＞0,ti≥0,hi＞0,i=1,2,···,n,及f∈K,設(shè)

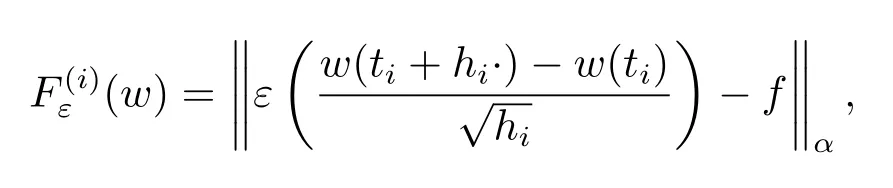
則存在一常數(shù)c=c(k,p,q1,f)＞0,對(duì)任意δ∈(0,1],ε∈(0,1],有

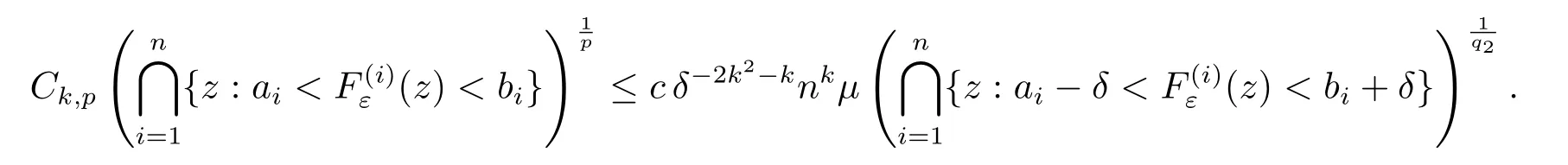
證利用引理2,類似文獻(xiàn)[6]中引理2.2易證.

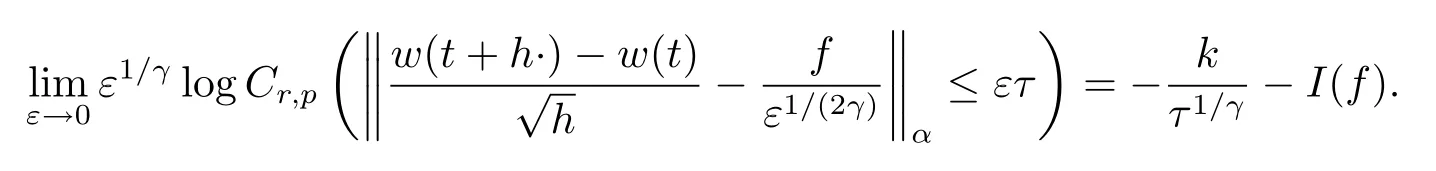
證考慮到容度具有性質(zhì)Cr,p(·)≥μ(·),結(jié)合(2)式只需證明

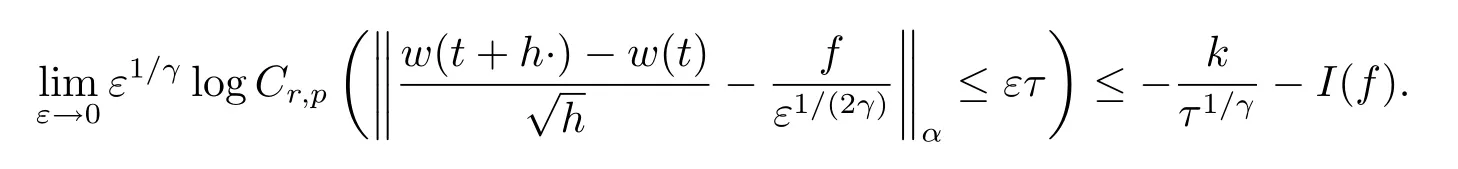
對(duì)任意1＞δ＞0,c0＞0,令k=[r]+1,根據(jù)引理3,有

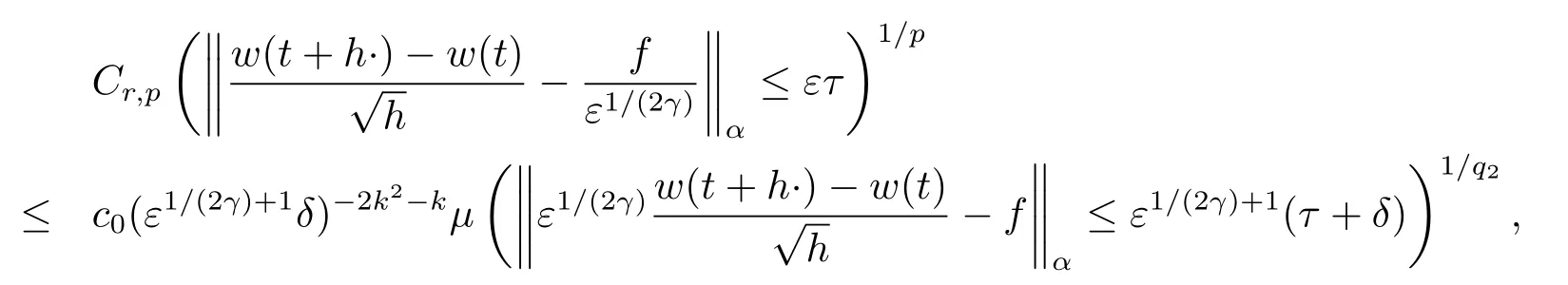
再根據(jù)(2)式得

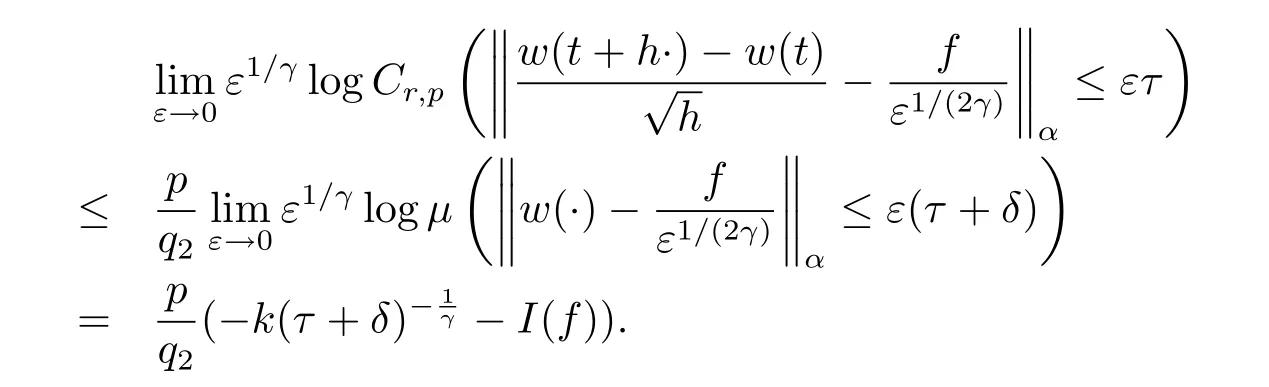
最后令δ→0,q2→p,引理4獲證.

引理5設(shè)ru,σu如命題1所定義,則對(duì)s∈[0,1]在Cr,p-q.s.意義下有

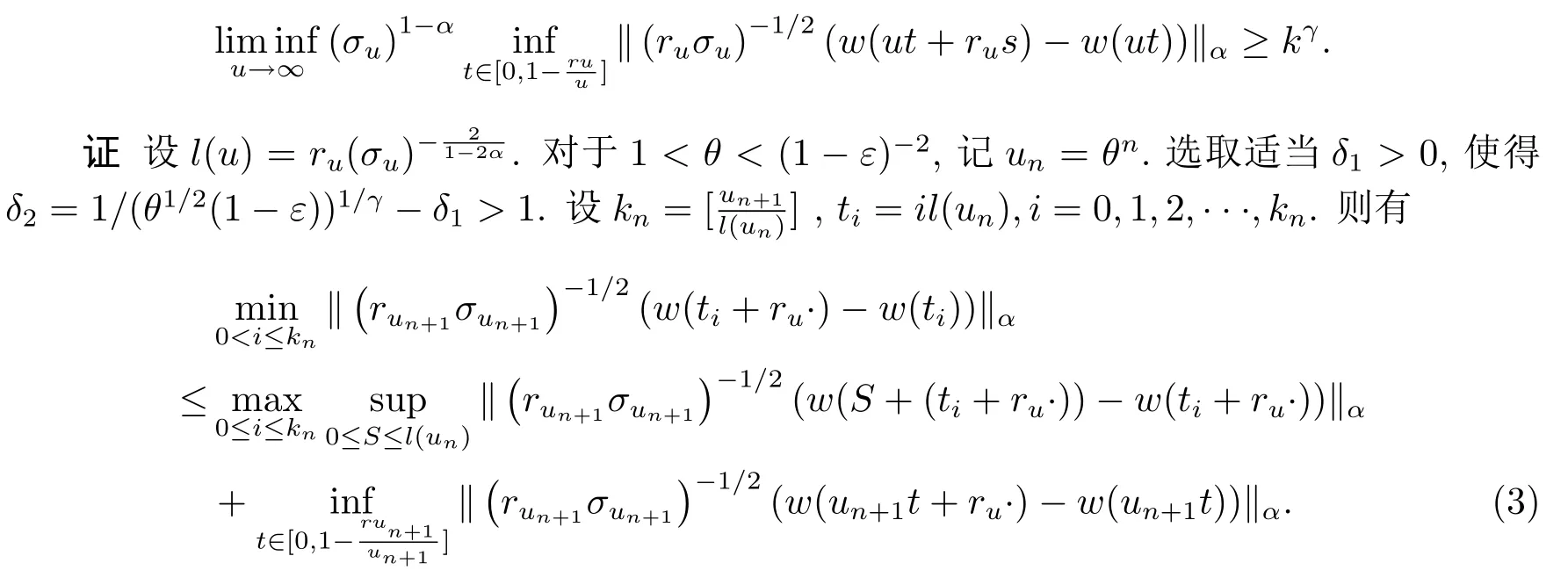
由引理4,對(duì)任意0＜ε＜1,當(dāng)n充分大時(shí)有

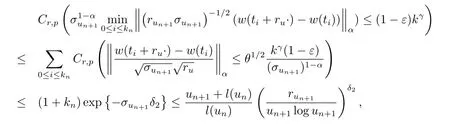
因此根據(jù)Borel-Cantelli引理得到在Cr,p-q.s.意義下有

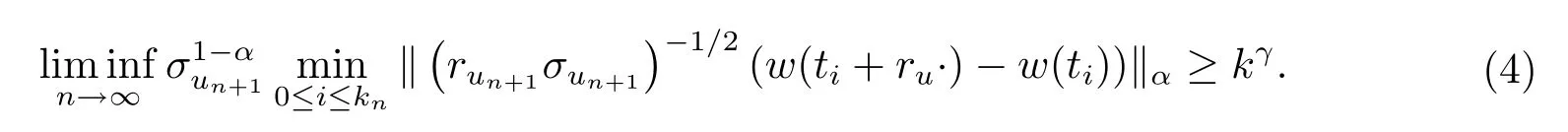
另一方面,對(duì)任意η＞0有

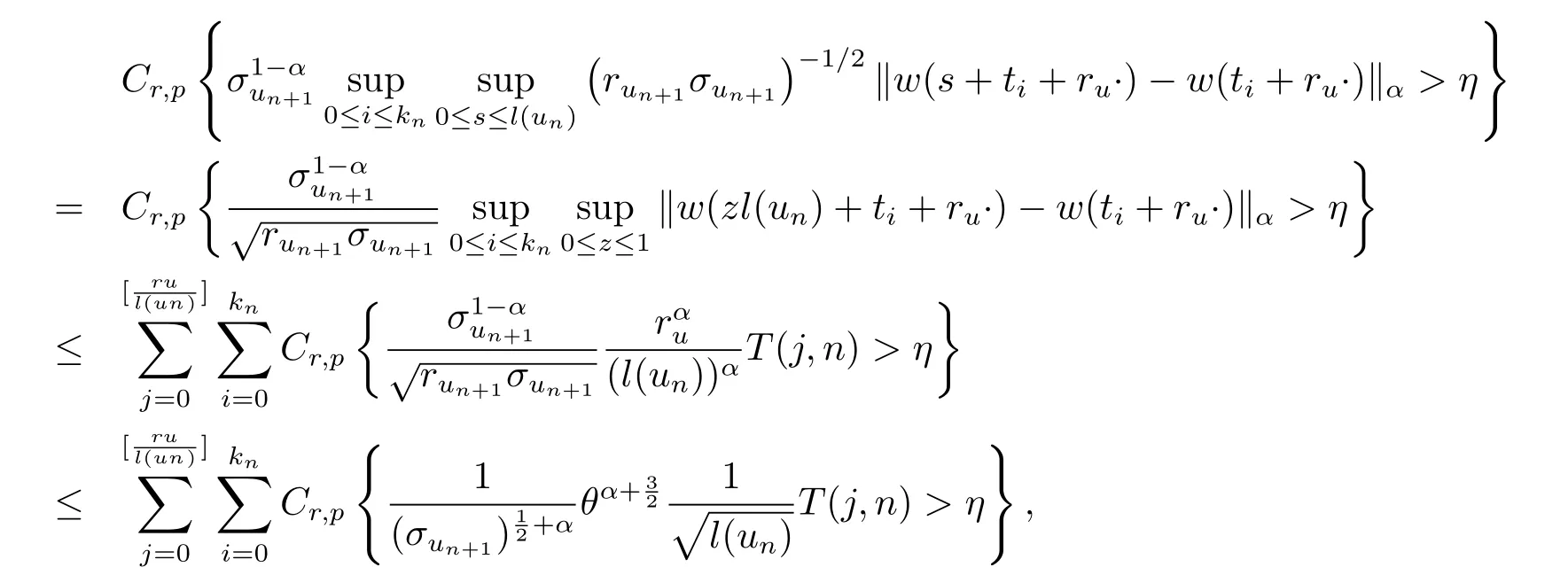
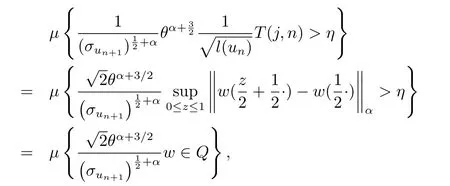
其中Q={f∈Cα,0;,故由引理1知當(dāng)n充分大時(shí)有

考慮到當(dāng)n→∞,σun+1→∞,因此

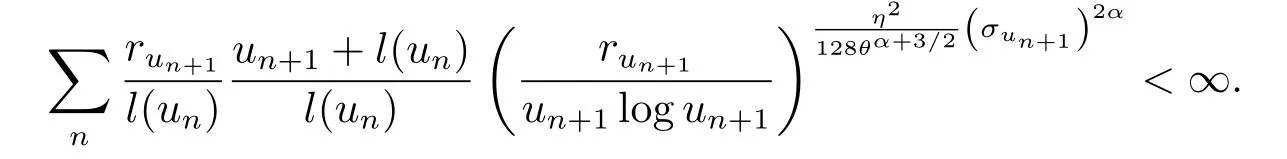
再次利用Borel-Cantelli引理可得在Cr,p-q.s.意義下有

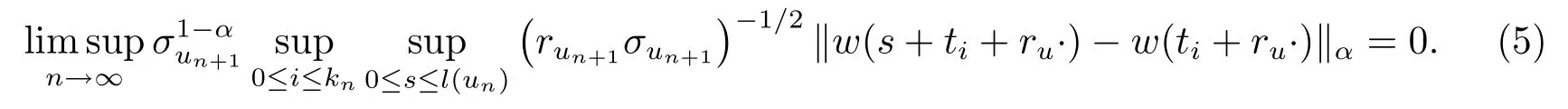
聯(lián)合(3),(4),(5)式得

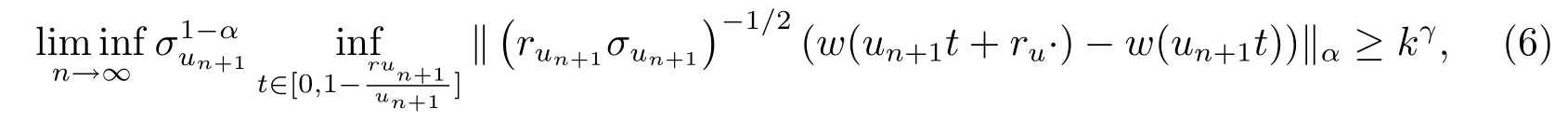
對(duì)于u∈[un,un+1),再設(shè)φt,u(s)=(ruσu)-1/2(w(ut+rus)-w(ut)),從而有

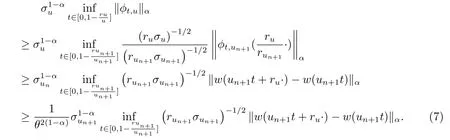
令θ→1,由式(6)、(7)證得在Cr,p-q.s.意義下有

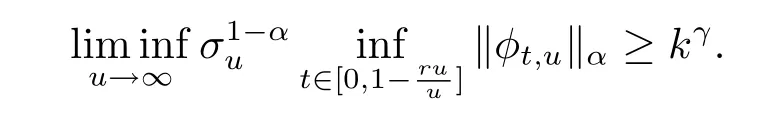
引理6設(shè)ru,σu如引理5中所定義,若=∞,則在Cr,p-q.s.意義下有

[1]Yoshida N.A large deviation principle for(r,p)-capacities on the Wiener space[J].Prob.The.Relat. Fields,1993,94(4):473-488.

[2]Baldi P,Roynette B.Some exact equivalents for the Brownian motion in Hlder norm[J].Prob.The. Relat.Fields,1992,93(4):457-483.

[3]Chen Xiong,Balakrishnan N.Extensions of functional LIL w.r.t.(r,p)-capacities on Wiemer space[J].Stat.Prob.Lett.,2007,77(4):468-473.

[4]Liu Jicheng,Ren Jiagang.A functional modulus of continuity for Brownian motion[J].Bull.Sci. Math.,2007,131(1):60-71.

[5]Wang Wensheng.A generalization of functional law of the iterated logarithm for(r,p)-capacities on the Wiener space[J].Stoch.Proc.Appl.,2001,96(1):1-16.

[6]Liu Yonghong,Li Luoqing.The rate of quasi sure convergence in the functional limit theorem for increments of a Brownian motion[J].J.Math.Analy.Appl.,2009,356:21-29.

[7]Baldi P,Ben A G,Kerkyacharian G.Large deviations and the Strassen theorem in Hlder norm[J]. Stoch.Proc.Appl.,1992,42(1):171-180.

[8]Deuschel M,Stroock D W.Large deviation[M].Baston:Academic Press,1989.

[9]張立新.布朗運(yùn)動(dòng)在(r,p)-容度意義下的下極限性質(zhì)[J].數(shù)學(xué)學(xué)報(bào),1996,39(4):543-555.

[10]危啟才.k-維Brown運(yùn)動(dòng)的泛函重對(duì)數(shù)定律[J].數(shù)學(xué)雜志,2007,27(4):405-410.

2010 MR Subject Classification:60F10;60F15;60F17

THE RATE OF LOCAL FUNCTIONAL CONVERGENCE FOR BROWNIAN MOTION'S INCREMENTS IN HLDER NORM

LI Yu-hui
(School of Mathematics and Computing Science,Guilin University of Electric and Technology, Guilin 541004,China)

In this paper,the local functional limit theorem for increments of a Brownian motion is derived.With large and small deviations,the local functional convergence rate for increments of Brownian motion in Hlder norm with respect to capacity is estimated,and the result in[4]is generalized.

Brownian motion;convergence rate;Hlder norm;capacity

MR(2010)主題分類號(hào):60F10;60F15;60F17O211.4

A

0255-7797(2016)06-1231-07

?2015-05-22接收日期:2015-12-23

國(guó)家自然科學(xué)基金資助(71162017);廣西自然科學(xué)基金資助(2014GXNSFAA118010).

李余輝(1981-),男,湖北咸寧,講師,主要研究方向:概率極限理論.