OPTIMAL EXISTENCE OF SYMMETRIC POSITIVE SOLUTIONS FOR A FOURTH-ORDER SINGULAR BOUNDARY VALUE PROBLEM
ZHANG Yan-hong
(School of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)
OPTIMAL EXISTENCE OF SYMMETRIC POSITIVE SOLUTIONS FOR A FOURTH-ORDER SINGULAR BOUNDARY VALUE PROBLEM
ZHANG Yan-hong
(School of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)
In this paper,we study a fourth-order singular boundary value problem.Using the Leggett-Williams fixed point theorem together with constructing a special cone,we establish optimal existence of symmetric positive solutions for a fourth-order singular boundary value problem under certain conditions,which generalizes optimal existence of symmetric positive solutions to singular boundary value problem.
symmetric positive solutions;boundary value problem;cone
2010 MR Subject Classification:34B15;34B25
Document code:AArticle ID:0255-7797(2016)06-1209-06
1 Introduction
We consider existence of symmetric positive solutions for a fourth-order singular boundary value problem:
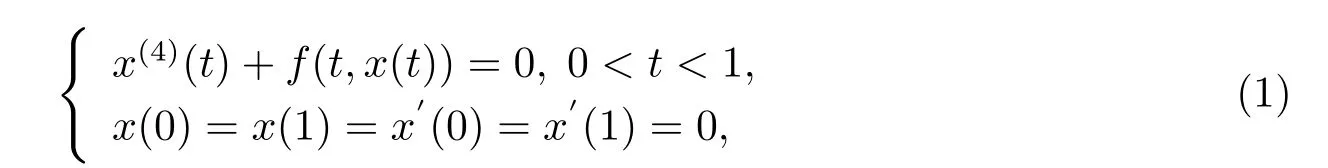
which describes the deformations of an elastic beam with both endpoints fixed,where f: (0,1)×(0,+∞)→(0,+∞)is conditions and f(t,x)=f(1-t,x)for each(0,1)×(0,+∞). f(t,x(t))may be singular at t=0 and/or t=1.
Here symmetric positive solutions for a fourth-order singular boundary value problem (1)satisfying x(t)=x(1-t)and x(t)>0,t∈(0,1).
Boundary value problems arise in a variety of different areas of applied mathematics and physics(see[1,2]and the references therein).Recently many authors studied the existence of positive solutions for four-order singular boundary value problems for example [3-13]and the references therein.Most of these results are obtained via transforming the four-order boundary value problems into a second-order boundary value problems,and thenapplying the Leray-Schauder continuation method,the topologial degree theory,the fixed point theorems on cones,the critical point theory,or the lower and upper solution method. However results about the existence of symmetric positive solutions to singular boundary value problem(1)are few.Motivated by the results in[9,11]we try to establish optimal existence of symmetric positive solutions to problem(1)by applying Leggett-Williams fixed point theorem.
2 Preliminary
We consider problem(1)in a Banach space C[0,1]equipped with the norm‖x‖=|x(t)|.A function x(t)∈C[0,1]is said to be a concave function if x(τt1+(1-τ)t2)≥ τx(t1)+(1-τ)x(t2)for all t1,t2,τ∈[0,1].We denote
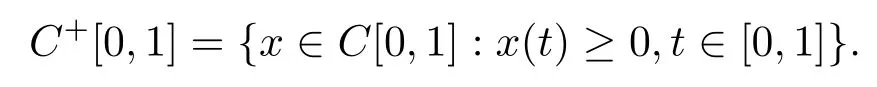
Let K be a cone of C[0,1]and m,n be constants,0<m<n.Define
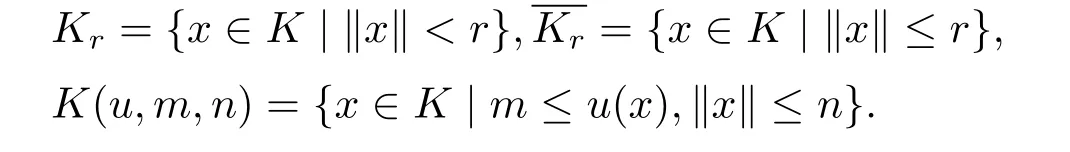
Let G(t,s)be the Green's function of the corresponding boundary value problem(1),i.e.,
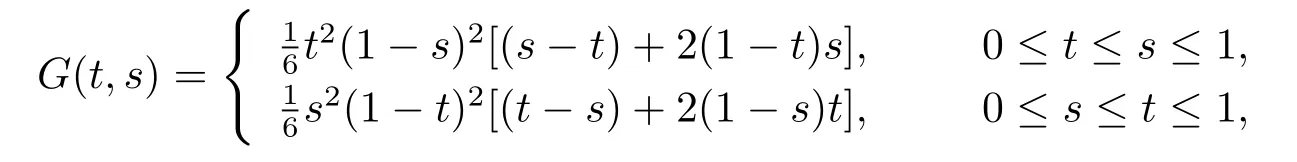
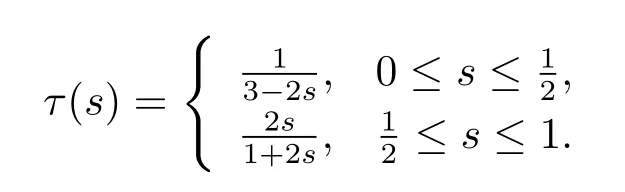
After a simple calculation,we get
(IV)(see[9])q(t)G(τ(s),s)≤G(t,s)≤G(τ(s),s),q(t)=min{t2,(1-t)2},t∈[0,1].
Lemma 2.1(see[14])Let A:K→K be a completely continuous operator,u be a nonnegative continuous concave function on K,and satisfies u(x)≤‖x‖for all x∈In addition,assume that there exist 0<d<m<n≤r satisfy the following conditions:
(iii)u(Ax)>m for x∈K(u,m,r)and‖Ax‖>n; then A has at least three fixed points x1,x2,x3onsatisfy‖x1‖<d,m<u(x2),and‖x3‖>d for u(x3)<m.
3 Main Results
Theorem 3.1 Suppose the following conditions hold:
(H1)f∈C((0,1)×[0,+∞),[0,+∞)),f(t,x)≤g(t)h(x),g∈C((0,1),[0,+∞)),h∈C([0,+∞),[0,+∞));
then problem(1)has triple symmetric positive solutions x1,x2,x3satisfy‖x1‖<d,m<u(x2),and‖x3‖>d for u(x3)<m.
Proof Denote K={x∈C+[0,1]:x(t)is convex function and x(t)=x(1-t),t∈[0,1]},then K is a cone of C+[0,1].
Define operator A:K→K by Ax(t)=G(t,s)f(s,x(s))ds.Obviously Ax(t)≥ 0,(Ax)''(t)<0 for 0<t<1,and for x∈K,
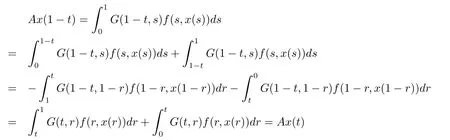
consequently Ax∈K,that is A:K→K.By Arzela-Ascoli theorem,we can prove A:K→K is completely continuous.
From(H1)and 3)in(H3),for any x∈we know that
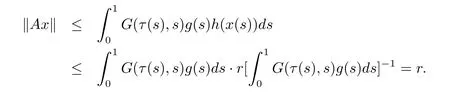
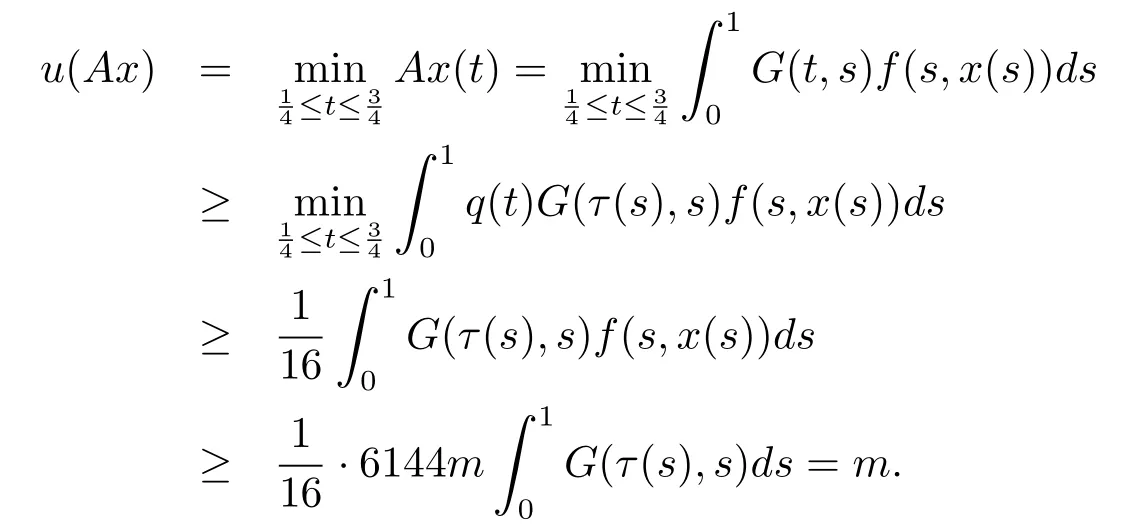
Thus condition(i)of Lemma 2.1 holds.
Next from(H1)and 1)in(H3),for any x∈we have
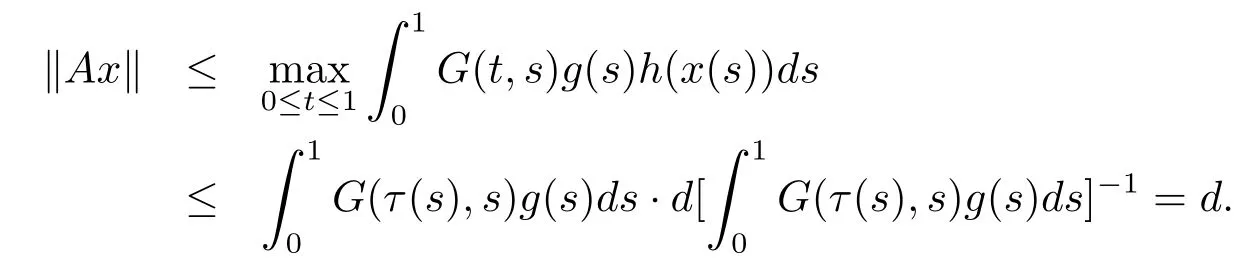
Finally we prove u(Ax)>m for x∈K(u,m,r)and‖Ax‖>4m.
From 2)in(H3),for x∈K(u,m,r)and‖Ax‖>4m,we know that
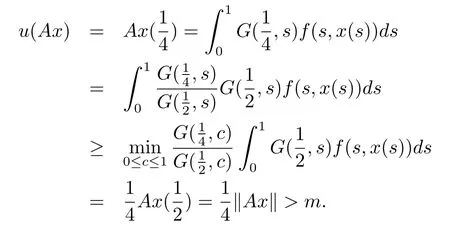
Therefore condition(iii)of Lemma 2.1 holds too.The proof is completed.
RemarkTheorem 3.1 also holds when nonlinearity f(t,x(t))is nonsingular at t=0 and t=1.
4 Example
Example 4.1The following boundary value problem:
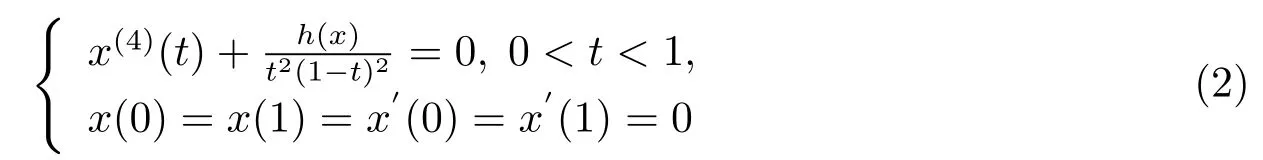
has triple symmetric positive solutions,where
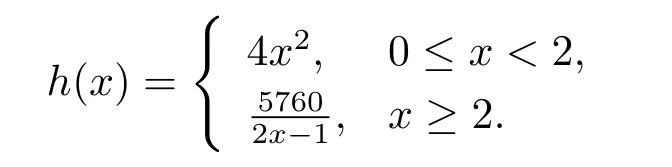
Proof Let f(t,x)=h(x)g(t),g(t)=Obviously g(t)is signular at t=0 and t=1.h(x)∈C[0,+∞).So(H1)holds.
Since
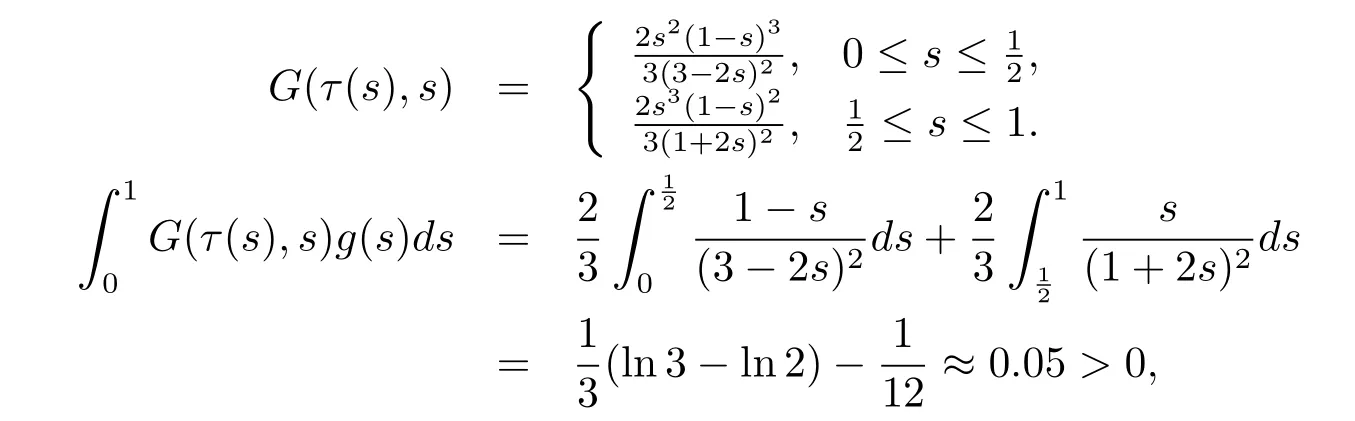
then(H2)holds.
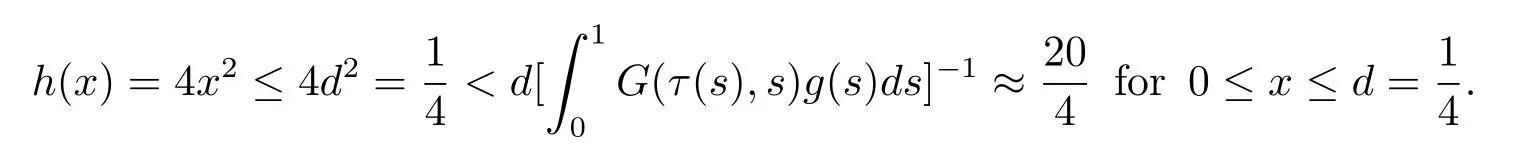
2)In(H3)is immediate,since we may take m=2 then
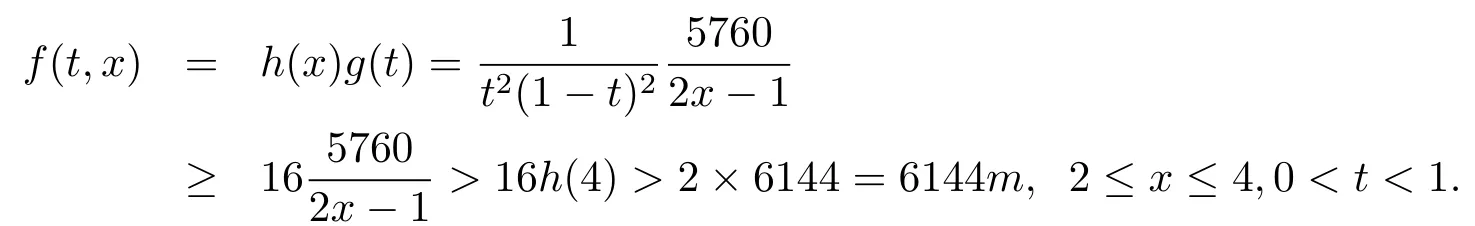
3)In(H3)is immediate,since we may take r=100>2m=4 then
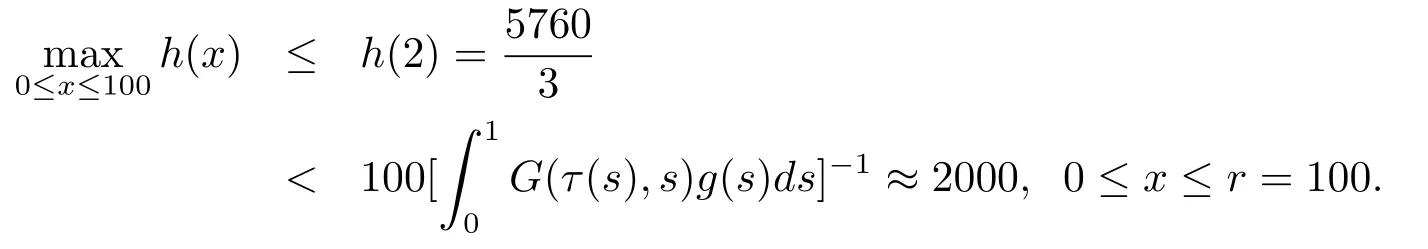
Thus from Theorem 3.1,we know that problen(2)has triple symmetric positive solutions x1,x2,x3satisfy‖x1‖<2<u(x2),and‖x3‖>for u(x3)<2.
References
[1]Davis J M,Erbe L H,Henderson J.Multiplicity of positive solutions for higher order Sturm-Liouville problems[J].Rocky Mountain J.Math.,2001,31:169-184.
[2]Liu L S,Sun Y.Positive solutions of singular boundary value problems for differential equations[J]. Acta Math.Sci.Ser.A.Chin.Ed.,2005,25(4):554-563.
[3]Tang Rongrong.A class of fourth-order nonlinear boundary layer solution of singular perturbation boundary value equation[J].J.Math.,2007,27(4):385-390.
[4]Alves E,Ma T F,Pelicer M L.Monotone positive solutions for a fourth order equation with nonlinear boundary conditions[J].Nonl.Anal.TMA,2009,71:3834-3841.
[5]Graef J R,Yang B.Positive solutions of a nonlinear fourth order boundary value problem[J].Comm. Appl.Nonl.Anal.,2007,14(1):61-73.
[6]Ma H L.Symmetric positive solutions for nonlocal boundary value problems of fourth order[J].Nonl. Anal.,2008,68:645-651.
[7]Liu B.Positive solutions of fourth-order two-point boundary value problems[J].Appl.Math.Comput.,2004,148:407-420.
[8]Ma R,Wang H.On the existence of positive solutions of fourth-order ordinary differential equations[J].Appl.Anal.,1995,59:225-231.
[9]Pei M,Chang S K.Monotone iterative technique and symmetric positive solutions for a fourth-order boundary value problem[J].Math.Comput.Model.,2010,51:1260-1267.
[10]Yang B.Positive solutions for the beam equation under certain boundary conditions,electron[J].J. Diff.Equ.,2005,78:1-8.
[11]Yao Q.Positive solutions for eigenvalue problems of fourth-order elastic beam equations[J].Appl. Math.Lett.,2004,17:237-243.
[12]Zhang X P.Existence and iteration of monotone positive solutions for an elastic beam with a corner[J].Nonl.Anal.RWA,2009,10:2097-2103.
[13]Jankowski T,Jankowski R.Multiple solutions of boundary-value problems for fourth-order differential equations with deviating arguments[J].J.Optim.The.Appl.,2010,146:105-115.
[14]Guo D J,Lakashmikantham V.Nonlinear problems in abstract cones[M].New York:Academic Press,1988.
一類四階奇異邊值問題對稱正解的最優(yōu)存在性
張艷紅
(福州大學(xué)數(shù)學(xué)與計算機科學(xué)學(xué)院,福建福州350108)
本文研究了一類四階奇異邊值問題.通過建立一個特定的錐,利用Leggett-Williams不動點定理,從而在一定的條件下得到一類四階奇異邊值問題對稱正解的最優(yōu)存在性,推廣了奇異邊值問題對稱正解的最優(yōu)存在性的結(jié)果.
對稱正解;邊值問題;錐
MR(2010)主題分類號:34B15;34B25O175
?date:2014-10-14Accepted date:2015-07-06
Supported by the Science and Technology Development Fund of Fuzhou University(2014-XQ-30).
Biography:Zhang Yanhong(1976-),female,born at Fuzhou,Fujian,associate professor,major in differential equation.

