門宏志,劉文龍,王　楠,金明錄

(大連理工大學信息與通信工程學院,遼寧大連 116023)

?

空間調制系統低復雜度的天線選擇算法

門宏志,劉文龍,王楠,金明錄

(大連理工大學信息與通信工程學院,遼寧大連 116023)

空間調制(Spatial Modulation,SM)是一種特殊的多天線傳輸技術,利用發(fā)送天線索引和發(fā)送的符號共同傳遞信息.為了獲得發(fā)送分集增益,人們將天線選擇技術應用到SM系統中,提高SM系統解調性能.在天線選擇技術中,最大-最小歐式距離(Euclidean Distance Antenna Selection,EDAS)準則應用較為廣泛,但是它的全搜索求解方法復雜度高,限制了其應用.為此,本文利用空間調制系統和調制符號本身的特性,從2維量化解調的視角出發(fā),給出了兩種低復雜度的最優(yōu)天線選擇算法,并通過計算機仿真和復雜度分析,表明了該算法的有效性和最優(yōu)性.

空間調制;天線選擇;低復雜度

1　引言

現代無線通信對數據傳輸速率和頻譜利用率的要求越來越高,多輸入多輸出(Multiple Input Multiple Output,MIMO)系統應運而生[1].然而,由于信道間干擾(Inter-Channel Interference,ICI),天線間同步(Inter-Antenna Synchronization,IAS)和多無線電射頻(Radio Frequency,RF)鏈路等問題,引起了MIMO系統成本和復雜度的不斷增加.空間調制(Spatial Modulation,SM)技術的出現解決了MIMO系統的上述局限.

SM系統解調不同于傳統MIMO系統的解調,不僅需要解調發(fā)送天線發(fā)送的符號,還需要判斷是由哪根天線進行發(fā)送的.激活天線的解調主要依靠發(fā)送天線信道間的差異,所以信道特性對SM系統解調的影響嚴重,需要盡可能地選擇信道特性較好的天線進行數據傳輸.所以各國學者提出了各種新的空間調制方案,主要包括開環(huán)[5～7]和閉環(huán)[8～10]兩種方案.天線選擇技術已經在傳統MIMO系統中被廣泛研究和應用[11～13],在提高系統性能上有良好效果,所以天線選擇技術被引入SM系統,受到學者們的關注.天線選擇的一個有效的準則是歐氏距離準則(Euclidean Distance Antenna Selection,EDAS),但全搜索的EDAS算法具有非常高的計算復雜度,限制了其應用.為此,多種低復雜度的次優(yōu)[14～15]和最優(yōu)[16～17]天線選擇算法相繼被提出.

文獻[14]的算法認為天線間信道增益矩陣的奇異值越小,其天線間歐氏距離越小.文獻[15]的算法認為發(fā)送符號的幅度越小,歐氏距離越小,因此只遍歷幅度最小的發(fā)送符號即可.在文獻[16]中,作者提出了一種低復雜度的EDAS(EDAS-LC)算法,利用QR分解和硬判決思想,降低算法的復雜度,同時保持了全搜索EDAS算法的最優(yōu)性.文獻[17]是在文獻[16]的基礎上,利用調制符號的鏡像對稱特性,進一步降低天線選擇算法的計算復雜度.這兩種算法只討論了MQAM調制的SM系統,沒有考慮MPSK調制的SM系統.然而,與非恒包絡調制(如MQAM)相比,恒包絡調制(如MPSK)能在功耗和能效方面提供更好的性能[2],因為其不要求嚴格的線性,使得功率放大器的功效不會受調制方式的線性要求的嚴重影響,減少發(fā)送端的發(fā)送功率.因此,基于恒包絡調制(比如MPSK)的SM技術必然擁有更大的優(yōu)勢[2].

本文基于調制符號固有的性質,并利用量化的原理,針對MPSK調制的SM系統,提出了兩種復雜度與調制階數無關的最優(yōu)天線選擇算法:EAQ-EDAS(Equal Amplitude and Quantization based EDAS)算法,利用MPSK各星座點符號具有相等的幅度的性質,簡化了EDAS準則,然后利用2-D量化原理,求得所需的選擇天線;RS-EDAS (Rotational Symmetry based EDAS)算法,利用調制符號本身的旋轉對稱性(RS),降低符號搜索空間的大小,進而降低算法的計算復雜度.兩種算法在降低EDAS算法復雜度的同時實現了最優(yōu)性能.

2　系統模型

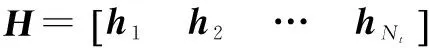
y=Hx+n=hls+n

(1)

(2)

S表示調制符號集合,且|S|=M.那么,EDAS準則就是:計算各個天線組合中歐氏距離的最小值,然后尋找所有天線組合的最小值中的最大值,該最大值對應的天線組合,就是應當選用的天線組合,即:

(3)

3　低復雜度的最優(yōu)天線選擇算法

3.1EAQ-EDAS算法

EAQ-EDAS算法利用了MPSK星座圖中各個星座點符號的幅度相等的特性.對于式(3)的EDAS準則,當i=j,s1≠s2時,可以表示為:

(4)

(5)

因為選擇的天線的序號i,j和發(fā)送符號s1,s2是獨立的,因此式(3)的內部優(yōu)化問題可以分解為先求解發(fā)送符號,再求解天線序號的嵌套優(yōu)化問題:

(6)

式(6)的求解可以分兩步,先求解給定i和j條件下的s1和s2,然后再對i和j求解.下面我們討論給定天線序號i,j的條件下,使得歐氏距離最小的s1,s2,即式(6)的內部優(yōu)化問題,等價于:

(7)

(8)

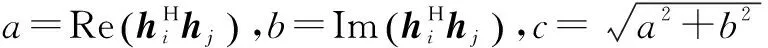
(9)

假設cosθi,j=a/c,sinθi,j=b/c,那么,根據三角函數積化和差公式,式(9)可以進一步化簡得到:

(10)

根據余弦函數的性質,當φ2-φ1+θi,j=0即φ2-φ1=θi,j時,式(10)取值最大值,且最大值等于c.但φ2-φ1∈{2π*k/M},k∈{-M+1,…,M-1},θi,j∈[0, 2π]所以大部分情況下φ2-φ1不可能等于θi,j,只能求得滿足條件且與θi,j最近的角度值.根據三角函數的性質,我們可以得到如下結論:

(11)

(12)

EAQ-EDAS算法總結如算法1

算法1EAQ-EDAS算法

end

fork=1:N

end

end

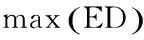
3.2RS-EDAS算法

RS-EDAS算法利用了旋轉對稱性,所以首先我們介紹旋轉對稱性的概念.

定義1(旋轉對稱性)假設復平面上有L個不同的點,等間隔的分布在同一個圓上,且圓心位于坐標原點,相鄰兩點之間的夾角為α(基本旋轉角),則稱這L個點彼此關于α旋轉對稱,這L個點構成的集合稱為旋轉對稱集合.

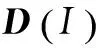
(13)

其中,Θ={1,2,…,N},Ii,Ij分別表示集合I中第i個和第j個元素對應的天線的索引.當i=j時,對于MPSK調制,可以求得|s1-s2|2的最小值為(2sin(π/M)2.當i≠j時,式(13)可以轉換成實數矩陣表示:

D(I)i,j=

(14)

其中,Re(·)和Im(·)分別表示變量的實部和虛部.定義

(15)

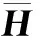
(16)

此時式(14)可以表示為:

(17)

(18)

(19)

通過上面的推導我們可以知道,在EDAS算法求最優(yōu)解過程中,只需對s2進行遍歷即可,s1可以根據式(19)直接獲得.那么如何簡單快速搜索s2就成為降低EDAS算法復雜度的關鍵.本算法利用旋轉對稱性降低符號s2的搜索空間,進而降低EDAS算法的復雜度.為此,我們先給出下面的定理.

=u1coskα-u2sinkα

=u2coskα+u1sinkα

(20)

所以同一個旋轉對稱集中只需要搜索一個星座點即可.MPSK星座圖中僅有1個旋轉對稱集,所以,MPSK調制下,符號搜索空間大小為1.根據上面的分析,RS-EDAS算法的搜索空間大小為nN2,其復雜度是全搜索EDAS算法復雜度的1/M2.

RS-EDAS算法總結見算法2

算法2RS-EDAS算法

2:forl=1:n

根據(16)式求解R

令s2為MPSK星座圖中任意一點,求解u1,u2,u

end

fork=1:N

end

ED(l)=min(Di,j)

end

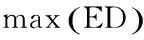
旋轉對稱性不僅是MPSK星座的性質,也是MQAM調制的特性,所以,基于旋轉對稱性的RS-EDAS算法一定可以用于MQAM調制的SM系統中.同樣定理1也適用于MQAM調制,所以,MQAM調制的SM系統符號搜索空間為M/4個元素.

4　仿真結果與分析

本節(jié)在不同參數下的SM系統中對提出的算法和幾種經典算法進行仿真,在所有仿真中我們都假設信道為瑞利衰落,噪聲為加性高斯白噪聲.

圖2仿真的系統參數為Nt=6,Nr=4,N=4.仿真結果表明:(1)相同的系統中,天線選擇技術可以降低系統的誤碼率,提高系統可靠性;(2)本文提出的兩種算法都具有最優(yōu)的性能;(3)文獻[15]算法在MQAM調制下不是最優(yōu)的,但在MPSK調制下是最優(yōu)的.

圖3仿真的系統參數為Nr=4,N=4SNR=10dB,8PSK調制.仿真結果表明隨著Nt的增加,本文提出的算法仍然具有最優(yōu)性能,同時相比于不進行天線選擇的SM系統性能要好很多.

圖4仿真的系統參數為Nt=6,N=4,SNR=10dB,8PSK調制.仿真結果表明隨著接收天線數的增加算法的性能越來越好,這是因為接收分集增益變大了.

圖5仿真的系統參數Nt=6,Nr=4,N=4,SNR=10dB,仿真點數為1000000.仿真時使用的是單核AMD Athlon 64 3500+處理器,核心速度1001.9MHz.仿真結果為了方便,采用了對數形式表示,結果表明全搜索DEAS算法復雜度與M2成正比;文獻[14]的算法與全搜索EDAS算法相比有一定的降低;文獻[15]的算法復雜度隨M線性增加;本文提出的兩種算法復雜度與M無關.

5　結論

在SM系統中,天線選擇技術是提高系統的性能的有效途徑.如何獲得最優(yōu)且低復雜度的天線選擇方案是當前研究的一個熱點問題.本文正是在這樣的背景之下提出了兩種低復雜度且最優(yōu)的天線選擇算法.兩種算法充分利用了調制符號本身的性質,MPSK調制符號的等幅性和旋轉對稱性,結合2-D量化原理,降低天線選擇算法的復雜度,同時不損失算法的性能.本文對提出算法的誤符號率性能和復雜度進行了詳細的分析和仿真,從理論和仿真兩個方面證明了兩種算法最優(yōu)性.

目前,大天線技術和綠色通信技術正受到業(yè)界的廣泛興趣,使用恒包絡調制信號(如MPSK)的SM 技術也受到關注,本文的提出的算法又對MPSK調制的SM系統有更強的優(yōu)勢,因此本文的算法有較好的實際應用意義.

[1]蘇彥兵,談振輝.基于天線選擇的低秩信道MIMO系統容量研究[J].電子學報,2004,32(3):395-398.

SU Y B,TAN Z H.Capacity of deficient rank MIMO channels with antenna selection[J].Acta Electronica Sinica,2004,32(3):395-398.(in Chinese)

[2]RENZO DI M,HAAS H,GHRAYEB ALI.Spatial modulation for generalised MIMO:challenges,opportunities,and implementation[J].Proceedings of the IEEE,2014,102(1):56-103.

[3]RENZO DI M,HAAS H,GRANT P M.Spatial modulation for multiple-antenna wireless systems:a survey[J].IEEE Communications Magazine,2011,49(12):182-191.

[4]RENZO DI M,HAAS H.Bit error probability of spatial modulation(SM-MIMO) over generalised fading channels[J].IEEE Transactions on Vehicular Technology,2012,61(3):1124-1144.

[5]RENZO DI M,HAAS H.Transmit-diversity for spatial modulation(SM):Towards the design of high-rate spatially-modulated space time block codes[A].IEEE International Conference on Communications[C].Kyoto,Japan:IEEE,2011.1-6.

[6]BASAR E,et al.Space-time block coded spatial modulation[J].IEEE Transactions on Communications,2011,59(3):823-832.

[7]RENZO DI M,HAAS H.On transmit-diversity for spatial modulation MIMO:Impact of spatial-constellation diagram and shaping filters at the transmitter[J].IEEE Transactions on Vehicular Technology,2013,62(6):2507-2031.

[8]WANG J L,et al.Closed-loop spatial modulation with antenna selection[A].IEEE International Conference on Signal Processing[C].Beijing,China:IEEE,2012.1291-1294.

[9]CHUNG W Ho,HUNG C Y.Multi-antenna selection using space shift keying in MIMO systems[A].IEEE Vehicular Technology Conference[C].Yokohama,Japan:IEEE,2012.1-5.

[10]YANG P,et al.Adaptive spatial modulation for wireless MIMO transmission systems[J].IEEE Communications Letter,2011,15(6):602-604.

[11]張廣馳,秦家銀.放大轉發(fā)MIMO中繼系統中的快速天線選擇算法[J].電子學報,2010,38 (1):68-73.

ZHANG G C,QIN J Y.Fast antenna selection algorithm in amplify and forward MIMO relay systems[J].Acta Electronica Sinica,2010,38 (1):68-73.(in Chinese)

[12]伍裕江,聶在平,樂鐵軍.基于極化可重構天線的天線選擇方案[J].電子學報,2007,35 (12):2252-2257.WU Y J,NIE Z P,LE T J.Antenna selection scheme based on polarization reconfigurable antenna[J].Acta Electronica Sinica,2007,35 (12):2252-2257.(in Chinese)

[13]楊亮,秦家銀.Nakagami-m Keyhole衰落信道下MIMO系統 容量及天線選擇[J].電子學報,2006,34 (1):107-109.

YANG L,QIN J Y.Capacity and antenna Selection of MIMO system over keyhole nakagami-m fading channels[J].Acta Electronica Sinica,2006,34 (1):107-109.(in Chinese)

[14]NTONTIN K,et al.A low-complexity method for antenna selection in spatial modulation systems[J].IEEE Communications Letter,2013,17(12):2312-2315.

[15]ZHOU Q,et al.Reduced-complexity antenna selection schemes in spatial modulation[J].IEEE Communications Letter,2014,18(1):14-17.

[16]RAJASHEKAR R,HARI K V S,HANZO L.Antenna selection in spatial modulation systems[J].IEEE Communications Letter,2013,17(3):521-524.

[17]PILLAYN,XU H.Comments on ‘Antenna selection in spatial modulation systems’[J].IEEE Communications Letter,2013,17(9):1681-1683.

門宏志女,1988年6月出生于吉林,大連理工大學信息與通信工程學院博士研究生,主要研究方向無線通信MIMO技術研究.

E-mail:menruiye@sina.com

劉文龍男,1973年11月生于遼寧,現任大連理工大學信息與通信工程學院副教授,博士生導師,主要研究方向為MIMO及SM系統檢測問題等.

E-mail:liuwl@dlut.edu.cn

王楠女,1989年11月生于吉林,2014年獲得大連理工大學通信與信息系統碩士學位,主要研究方向為MIMO系統、空間調制系統檢測算法研究.

E-mail:alisadlut@163.com

金明錄男,1958年2月出生于吉林,先后在日本、韓國和澳大利亞等國家訪問工作,現任大連理工大學信息與通信工程學院教授,博士生導師,主要研究方向為信號與通信系統基礎理論與技術.

E-mail:mljin@dlut.edu.cn

Low-Complexity Antenna Selection Algorithms for Spatial Modulation Systems

MEN Hong-zhi,LIU Wen-long,WANG Nan,JIN Ming-lu

(TheSchoolofInformationandCommunications,DalianUniversityofTechnology,Dalian,Liaoning116023,China)

Spatial modulation (SM) is a special multi-antenna transmission technology,where the transmit antenna index is exploited to convey information except for modulation signals.In order to obtain transmit-diversity gains,antenna selection technology is introduced in SM systems to increase its demodulation performance.In antenna selection technology,Euclidean distance antenna selection (EDAS) is widely applied.However,its exhaust-search detection has extremely high complexity,which limits its application.Thus,exploiting the characteristics of modulation symbols and 2-D quantization,two low-complexity and optimal antenna selection algorithms are proposed.The simulation results show that the proposed algorithms reduce the computational complexity meanwhile achieving optimal performance.

spatial modulation (SM);antenna selection;low complexity.

2014-09-01;修回日期:2014-12-11;責任編輯:梅志強

國家自然科學基金(No.11372069);遼寧省自然科學基金(No.2013020033)

TN911.23

A

0372-2112 (2016)06-1322-06