Sayed Ahmad Hosseini and Mohammad Mahdavi

Physics Department,University of Mazandaran,P.O.Box 47415-416,Babolsar,Iran

1 Introduction

There has been considerable interest in recent years in the field of electromagnetic Weibel instabilities due to their important role in generating quasi-stationary magnetic fields in laboratory[1?2]and astrophysical plasmas.[3]In fusion plasmas(Inertial confinement fusion plasma)it is well known that decreasing the laser wavelength increases the critical density of the target plasma.Consequently,energy is deposited more deeply onto the fusion target.The thermal energy flows from the deposition region into the target interior,where,the heat flow can be a ff ected by the magnetic fields resulted from the growing Weibel like instabilities.[4?6]More studies,in the field of Weibel like instabilities,have been structured in un-magnetic field free plasma.[7?9]These instabilities can develop both un-magnetic field free plasmas and magnetized plasmas.[10]Also,the non resonant instabilities can be certainly a ff ected because of the resonant instability resulted due to the cyclotron resonance with plasma particles.Studies,in the field of the inertial confinement fusion,show the spin polarized DT fuel can be effective on decreasing the required driver energy by increasing the cross-section of an effective fusion reaction.[11?12]In addition,it is well known that the Coulomb collisions are considered the basic mechanism of the absorption of the high frequency electromagnetic radiation.So,this can be important in coupling the laser energy to the plasmas when the short-wavelength lasers have been considered.Therefore the purpose of this paper is studying the electromagnetic Weibel modes in a magnetized fuel plasma in the presence of the Coulomb collisions.In Sec.2 the mathematical model and Weibel dispersion relation will be derived.Our discussion and conclusions are presented in Sec.3.

2 Mathematical Model and Dispersion Relation

The dynamics of system have been described by the non relativistic Boltzman equation(the Vlasov equation with a collision term)combined by the Maxwell equations which are:

Assuming linear transverse waves in a dense plasma composed of electrons and immobile ions,ions only act as a fixed neutralizing background and do not contribute to the Weibel unstable modes because of their larger mass and

where f=F+ δfω,kis the electron distribution function sum of the equilibrium and the perturbed distribution functions respectively,at momentumand positionat time t.The quantities m and q= ?e are the rest mass and charge of electron,respectively.andcontributed in the Lorentz force,are the perturbed electric and sum of the background and perturbed magnetic fields,respectively.The time evolution of the electron distribution function due to the effective Coulomb collisions,(δF/δt)coll,has been replaced by the lower temperature than that of electrons species.Therefore,the linear dispersion relation of the unstable Weibel modes will be derived only by solving the non relativistic Boltzman equation relevant to the time evolution of the electrons distribution functions:“Crook” simplicity term ?ν(f ?F),where ν is the background Coulomb collision frequency.The components of the perturbed magnetic field are described by the following expressions;[13]

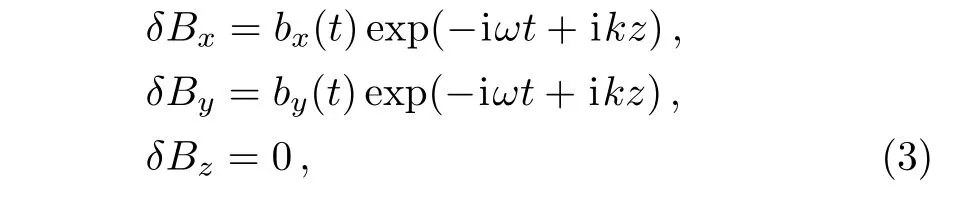
where the perturbed values vary as exp(?iωt+ikz)for each mode(k,ω),with the wave number,k,propagated to the z-axes of the coordinate system and the wave frequency,ω.It is assumed the background magnetic field is directed along the z-axis,since the x-and the y-axis are considered in perpendicular plane.The quantities bx,y(t)are describing the magnetic field amplitudes where their time variation will be smaller than that of the exponential part.For simplicity,let us follow Pokhotolov’s method,where the linearized Boltzman equation can be expressed as follows:[14?15]

The indexes∥and⊥are describing the parallel and perpendicular directions to the propagation of the wave number of the unstable modes.For a symmetric equilibrium velocity distribution function,the components of the magnetic field are considered equal.The quantity ωcis the electron cyclotron frequency while the quantity α is the pitch-angle where vx=v⊥cos(α)and vy=v⊥sin(α).Using the perturbed distribution function in form;δfω,k=exp(?iα)(the ? sign corresponds to the clock-wise(right-hand)or anti-clockwise(left-hand)rotation of the wave polarization plane),it can be derived as:

where ω′is sum of the frequency of unstable wave and electron-background(ions)collision in complex plane;i.e.ω′= ωr+i(ωi+ ν).Calculating the current density and linearizing the Ampere low by the non relativistic Maxwell equations,the general dispersion function can be obtained by following;

The mechanism of the Weibel instability depends on the stored free energy in the velocity space where,an anisotropic particle distribution will be governed in the velocity space(temperature anisotropy).[16?18]In this order,let us assume the perpendicular temperature dominates over the parallel so that in this direction,the particles tend to relativistic properties.Therefore,it can be possible,to describe the distribution function as semi-relativistic:[19]

where n is the plasma number density,and=is the thermal velocity of electrons in the vertical(parallel)direction.

Substituting Eq.(7)in Eq.(6)and making integrating as well as ignoring the contribution of the smaller sentences,we obtain

The relativistical parameter,μ,is defined as

and Z(ξ)is the plasma dispersion function as follows

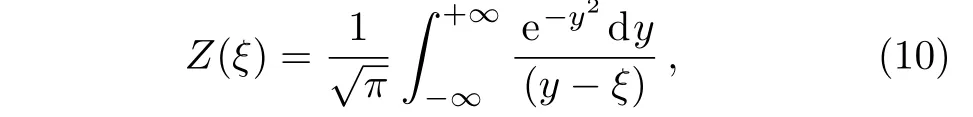
with ξ=((ω′± ωc)/kvT∥)and y=v∥/vT∥.The resonant unstable modes are usually described by those arguments of the plasma dispersion function which are comparable to unity or less,((ω ?ωc)/kvT∥) ≤ 1.The non resonant instability such as the Weibel mode should be defined in the very large and the very small arguments of the plasma dispersion function so that the growth rate of the unstable modes can be larger than their oscillation frequency.For large arguments of the plasma dispersion function,Eq.(8)only includes real statements that are not able to represent the growth rate and oscillation frequency.Therefore,let us continue for low-frequency limit,|ξ=((ω′± ωc)/kvT∥)|? 1,where Z(ξ)can be approximated as:

Replacing this approximation,(Eq.(11)),in Eq.(8),the imaginary part of frequency as the Weibel instability growth rate,(δ=Im ω),and the real frequency as the oscillation frequency,can be calculated as,respectively;

The effective collision frequency,ν,is the sum of the total frequency of different collisions that will occur among particles plasma(ν = νei+ νee+ ···).But the goal of this paper is to investigate the Coulomb collision effect of electron-ion;[20]since:

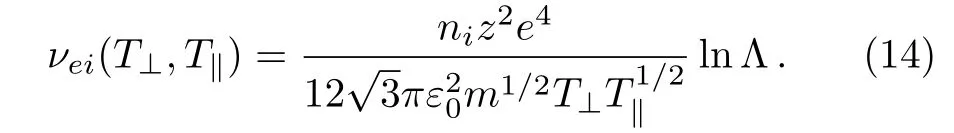
Finally,the Weibel instability growth rate can be derived as follows

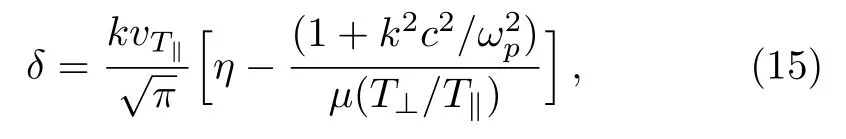
where

whenμ=η=1,the obtained conditions are supported for the unmagnetized collision less bi-Maxwellian plasma.

3 Discussion and Conclusion

In this paper,the Weibel instability has been studied in a dens magnetized plasma.In that case the Coulomb collision effects of the electron-background ions play an important role.In this order,analytical expressions are derived for the growth rate,also the oscillation frequency and the condition restricted unstable mode arguments in the low frequency limit of the plasma dispersion function.The obtained results imply the dependence of the oscillation frequency on the electron cyclotron movement frequency.So,the growth rate of the unstable modes is only relevant to the temperature anisotropy fraction,the collision(η)and the relativistic parameters,(μ).The growth rate normalized to ωp,(δ/ωp),are shown in Figs.1 and 2 for different η and μ with respect to ck/ωp.It is shown that the growth rate of Weibel instability will be increased by increasing the collision term due to decreasing the Coulomb collision frequency,which is equivalent to increasing the plasma temperature.With the advent of the relativistic quantity,μ,and its gradual increase even in the presence of high levels of collision frequency,it is equivalent to a reduction in plasma temperature.The growth rate will be increased in comparison with a nonrelativistic plasma and the absence of external magnetic

The parameter η as an effective parameter due to collision effects,leads to limiting the condition for the Weibel instability growth rate compared with the mode without collision effects.The oscillation frequency has been obtained in the rang of the electron cyclotron frequency.So in that case it is expected that the non resonant unstable modes only be present when the growth rate is much larger than the cyclotron frequency.While similar to unmagnetized plasma,for the small values of the cyclotron frequency,the Weibel instability can be a purely growing mode.Regarding this condition,the restricted condition on the Weibel modes can be derived by if eld.[13]Also,the variations of the growth rate normalized to ωp,(δ/ωp),according to ck/ωpare shown in Fig.3 for different values of T⊥/T∥in the limit η =0.58.The temperature anisotropy,T⊥/T∥,will be decreased due to applying a background magnetic field vertically along the propagation axis.Thus,the background magnetic field leads to decreasing the Weibel instability growth rate.

Fig.1 Variation of the normalized growth rate,δ/ωp,versus ck/ωpfor different μ in the limit η =0.38.

Fig.2 Variation of the normalized growth rate,δ/ωp,versus ck/ωpfor different η in the limit μ =100.

Fig.3 Variation of the normalized growth rate,δ/ωp,versus to ck/ωpfor different values T⊥/T∥ in the limitsμ=4 and η=0.58.

[1]A.Sid,A.Ghezal,A.Soudani,and M.Bekhouche,Plasma Fusion Res.5(2010)007.

[2]N.G.Zaki,Pramana-Journal of Phys.75(2010)4.

[3]P.Romatschke and R.Venugopalan,Phys.Rev.Lett.96(2006)062302.

[4]A.Raven,O.Willi,and P.T.Rumsby,Phys.Rev.Lett.41(1978)554.

[5]A.Raven,et al.,Appl.Phys.Lett.35(1979)526.

[6]M.D.J.Burgess,B.Luther-Davies,and K.A.Nugent,Phys.Fluids 28(1985)2286.

[7]S.Zaheer and G.Murtaza,Phys.Plasmas 14(2007)0221080.

[8]S.Zaheer and G.Murtaza,Phys.Plasmas 14(2007)072106.

[9]K.Estabrook,Phys.Rev.Lett.41(1978)1808.

[10]M.Lazar,R.Schlickeiser,and S.Poedts,Phys.Plasmas 16(2009)012106.

[11]M.Temporal,V.Brandon,B.Canaud,J.P.Didelez,R.Fedosejevs,and R.Ramis,Nucl.Fusion 52(2012)103011

[12]R.Kulsrud,et al.,Phys.Plasma 12(2005)082301.

[13]T.B.Yang,et al.,Phys.Plasmas 1(1994)9.

[14]K.Huang,Statistical Mechanic,Wiley,New York(1987).

[15]O.A.Pokhotelov and M.A.Balikhin,Ann.Geophys.30(2012)1051.

[16]E.S.Weibel,Phys.Rev.Lett.2(1959)83.

[17]B.Shokri and M.Ghorbanalilu,Phys.Plasmas 11(2004)5398.

[18]M.Mahdavi and H.Khanzadeh,Phys.Plasmas 21(2014)062708.

[19]M.Mahdavi and H.Khanzadeh,Commun.Theor.Phys.6(2014)127.

[20]M.Mahdavi and H.Khanzadeh,Phys.Plasmas 20(2013)052114.