SUN Shi-li,HU Jian,SUN Yi-long

(1 State Key Laboratory of Ocean Engineering,College of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2 College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China;3 China Ship Development and Design Center,Shanghai 200240,China)

0 Introduction

It is an old subject to analyze ship motions in waves or compute the hydrodynamic forces of prescribed body motion.Most of the research work is limited to the diffraction and radiation problem about those structures whose boundaries are almost perpendicular to the free surface such as the hemispheres or rectangular boxes.But most of surface ships or other surface structures have oblique boundaries,and thus the analysis on the hydrodynamic coefficients of the structures with oblique boundaries is urgent.A variety of analytical and numerical methods have been developed over the past few decades,the most famous of these are the Kelvin source model and the Rankine source model.The Rankine source model[1-2]should set panels on all its boundaries,but the form of its Green function is simple.This model has been used in many hydrodynamics problems with large and curved free surface elevations[3-4].The Kelvin source model is based on time domain Green function and only need set panels on body surface,but this is rather complex and its value is hard to be obtained.On this purpose,the solution for time domain Green function has been researched by many others[5-6],which make the use of time domain Green function method become possible.Lin and Yue[7]computed the hydrodynamic force on a hemisphere and a Wigley hull using time domain Green function method.Sen[8]presented a time domain computation for a Wigley hull with forward speed in wave and analyzes the influence of nonlinearities on the results.Singh and Sen[9]reported on 3D time domain seakeeping computations of a Wigley hull at different level of modeling of nonlinear effects.Dong[10]employed time-domain Green function method to compute the wave forces exerted on a hemisphere which accelerates the calculation by tabulating the Green’s function and its derivatives,interpolating their values on the grid during run time.However,this time domain Green function method is singular and highly oscillatory and thus it is hard to be used in diffraction and radiation problem of large flattering structures such as wedge-shape structures,conical structures or ships with large oblique boundaries due to its divergence,which has been analyzed by Chen and Wu[11].The divergence does not exist for straight-wall structure no matter the frequency of the structure is high or low.As a result,the method is greatly used in the hydrodynamic force of straight-wall structure such as hemisphere,rectangular box or those whose boundaries are most perpendicular to the free surface such as Wigley hull.But large flattering structures exist everywhere which makes the application of time domain Green function method limited.Frequency domain Green function has either been approximated by Newman[12]and similar work is done by Wang[13].

Most people think that divergence of diffraction and radiation problem using time domain Green function method is due to the singularity and highly oscillatory properties of free-surface Green function.Chen&Duan[14]and Chen,Duan&Lu[15]computed free-surface Green function considering surface tension and fluid viscosity indeed making the singularity of it disappears and it is an important progress for time domain Green function method.But for large flattering structures, the hydrodynamic force is still divergent using the method considering surface tension and fluid viscosity.After analyzing,the paper found that the divergence is induced by the high-frequency part of gravity waves.So,the paper filers the gravity waves induced by a source point on the large flattering structures to remove the high-frequency part and leave low frequency part through an algorithm based on the method by Chen,Duan&Lu[15],takes the three dimensional conical structures as an example,compares the result in the paper with that of the conventional method and determines the convergence condition of hydrodynamic coefficients.

1 Numerical procedures

1.1 Governing equation and boundary conditions

We consider the problem of heaving motion of a cone,as shown in Fig.1.The water surface is initially calm.A Cartesian coordinate system O-xyz fixed in the space is defined,in which x,y are along the undisturbed free surface and z points upwards and passes through the tip of the cone.The deadrise angle of the cone is defined as α,as shown in Fig.1.A is the amplitude of the heaving motion.And H is vertical length of the cone below the free surface when it stays at its equilibrium position.The fluid is assumed to be incompressible and inviscid,and the flow to be irrotational.

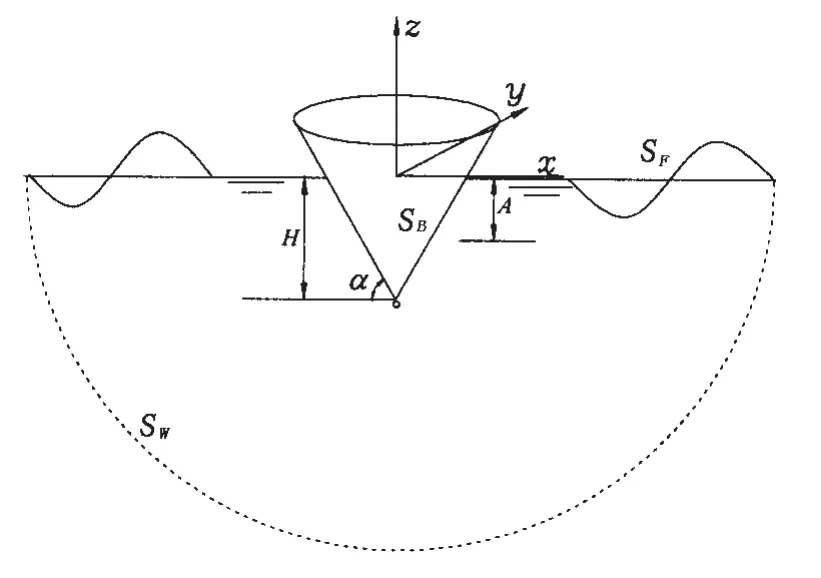
Fig.1 Sketch of the problem

For the entire fluid domain,Laplace(continuity)equation is applied as a governing equation

On the free surface,linear boundary condition should be satisfied

where g is gravity acceleration.On the cone surface,we have

where V is velocity of the cone.At the infinity

The initial boundary condition is

If this radiation problem is calculated by time-domain Green function method,the above boundary conditions must be satisfied.But,the time-domain sources are only needed to be placed on body surface SB.The influence of the free surface SFand the infinite radiation boundary Swis represented by linear time-domain Green function.Thus the form of linear time-domain Green function is rather complex.

1.2 Linear time-domain Green function considering surface tension and fluid viscosity

The linear time-domain Green function satisfying Eqs.(1-5)is given by:

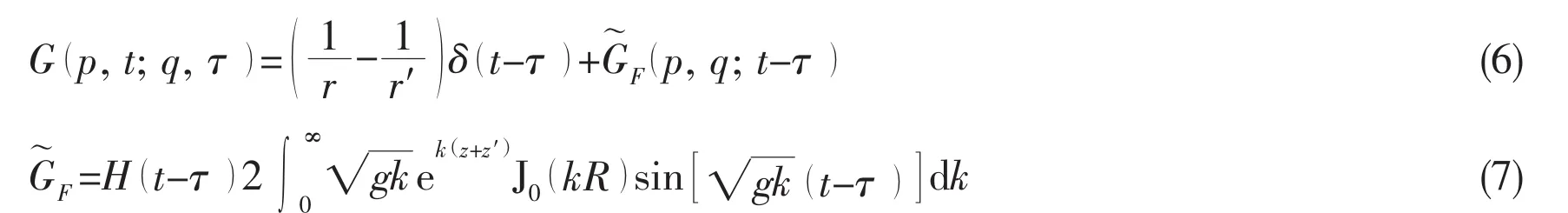
As a result,Chen,Duan&Lu[15]gave a new form of free surface Green function considering surface tension and viscosity which is written as

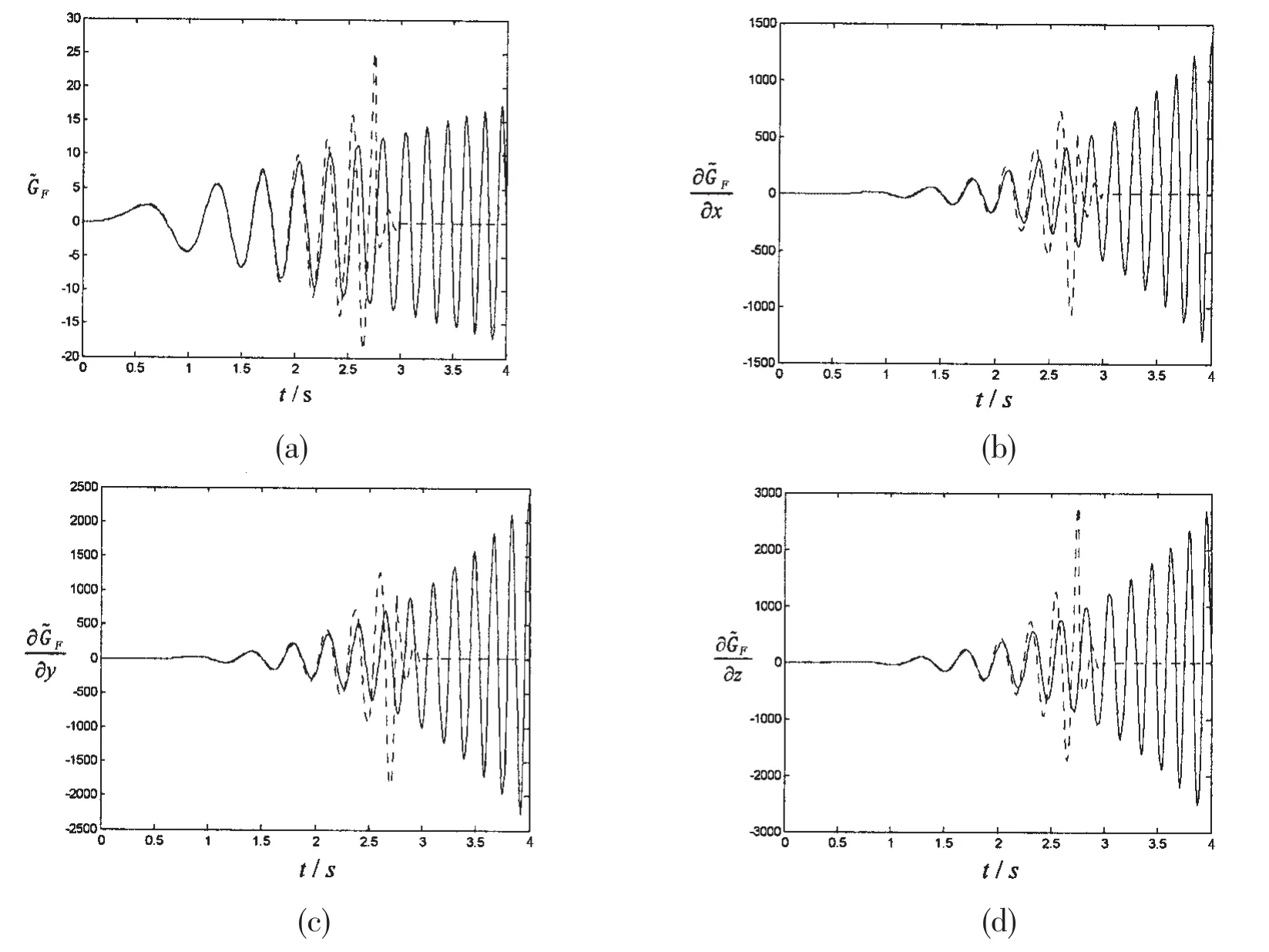
Fig.2 The change ofand its partial derivatives along t(v=0.000 01,h=0.5,solid line:Eq.(7),dashed line:Eq.(8))

Although the singularity disappears by taking the surface tension and viscosity into account,the hydrodynamic forces using the free surface Green function are still divergent sometimes especially for those structures with low-frequency heaving motion,the hydrodynamic force using Chen’s method is still divergent.That means the radiation problem of large flattering structures with low-frequency heaving motion is divergent using free-surface Green func-tion method considering surface tension and viscosity.For other conditions,whether the method can be used or not needs further researches.The divergence problem is so important that it influences the application scope of linear time-domain Green function method.Based on the above reasons,the paper gives a filtering method to resolve the divergence problem on the method by Chen,Duan&Lu[15].

1.3 Filtering scheme

The singularity disappears but the highly oscillatory property is not completely vanished by taking account of the viscosity and surface tension.From Fig.3,we can see that the frequency ofdecreases along time which means the free surface Green function changes from low frequency to high frequency,and then the high-frequency part disappears.Maybe,the divergence problem has already happened before the disappearance.So the main idea of the filtering scheme is removing the high-frequency part of free surface Green function and leaving low-frequency part according to the frequency of the motion and the shape of the structure.For different radiation problems,the degree of filtering is greatly different.The paper gives a reference quantity β,it represents the ratio of the frequency of gravity-dominate wave and that of the motion.

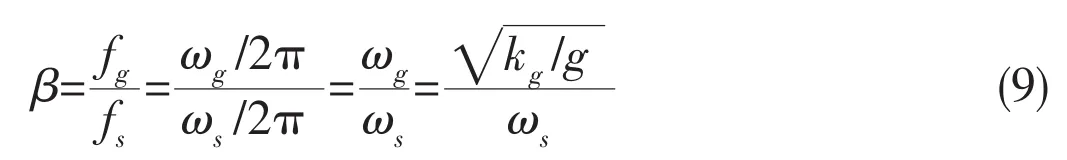
Fig.3 β changes along with time

where fg,ωgand kgare the frequency of gravity-dominate waves which change along with time,fsand ωsare the frequency of the prescribed motion which does not change along with time.In the paper,we denote the heaving motion as the prescribed motion.For radiation problem,ωsis already known.If we want to get the magnitude of β,kgmust be calculated first.kgcan be obtained through the following equation

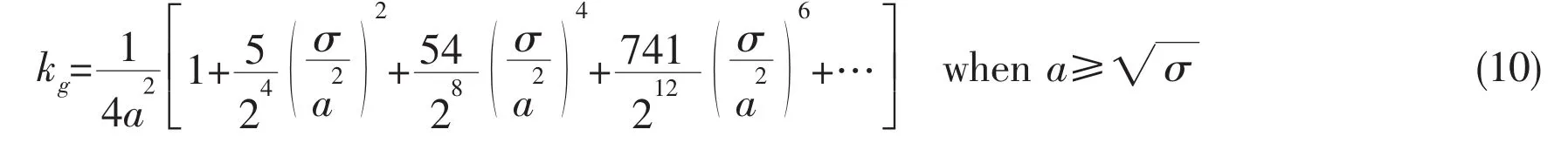
The filtering coefficient curve of β is as the Fig.3.

When β is greater than a certain value β0,the gravity-dominant wave decreases to zero.In the paper,we define β0as the filtering coefficient

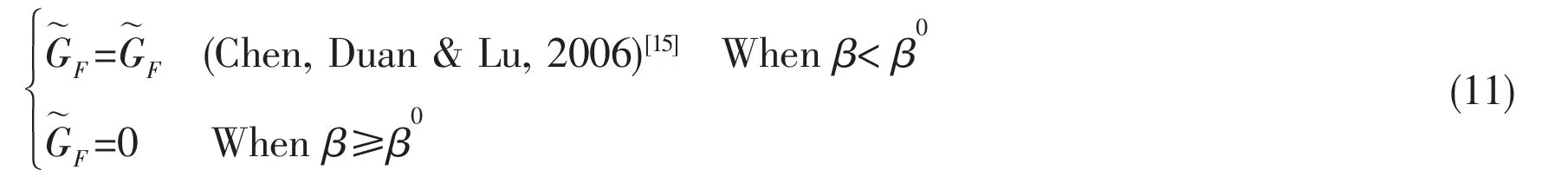
The most critical problem is how to choose the filtering coefficient β0.From the paper’s research,β0is influenced by many factors such as the frequency of the motion,the amplitude of the motion,the shape of the structure,and so on.The main purpose of this paper is determining the reasonable β0to guarantee the convergence of the radiation problem.In the paper,it denoteas the most reasonable β0and it only discusses the heaving motion of the conical structure.

2 Numerical result

2.1 Small-amplitude heaving motion

In the paper,a heaving cone with α=45°is taken as an example to analyze the influence of the filtering coefficient β0on the convergence property of the hydrodynamic force.The result for heaving amplitude A/H=0.05 is given in Fig.4 which is small enough.Through this figure,it can be seen that the hydrodynamic force is convergent for β0≤2.5 and divergent for β0≥3.5.The optimum filtering coefficientmust between 2.5 and 3.5.Meanwhile,although the result is convergent when β0is 0.5 or 1.5,the numerical result of them is larger than that of β0is 2.5.That is because the filtering degree is a little greater when β0is 0.5 or 1.5.As a result,the precision may be influenced if the filtering degree is excessive although the result is convergent which means β0can not be too small.The magnitude of β0can not be too larger either.If the filtering coefficient β0is too large,the filtering degree is light,the divergence problem may happen.Thus,choosing a reasonable β0is urgent.It should be noticed that the filtering method is reasonable for that the high-frequency part of wave acting on a structure indeed can not make the structure having larger displacement.So high-frequency wave can not make the structure generating great hydrodynamic force.

The method still needs further proof for obtaining a reasonablewhich can ensure both the precision and the convergence.Thus the added mass and damping coefficient by method in the paper are compared with that by frequency-domain Green function method.The divergence problem does not exist for frequency-domain Green function method.Because this method does not need computation in the time-domain.From the above analysis,it judges thatis be-tween 2.5 and 3.5.But from Fig.5,the result in the paper is most close to the added mass using frequency-domain Green function when β0is between 2.5 and 3.if β0is greater than 3,the result of added mass began showing divergent trend.So the scopeis further reduced.Now,is between 2.5 and 3.When β0is between 2.5 and 3,both added mass and damping coefficient do not change violently along β0and are very close to that by frequency-domain Green function.When β0is 2.5,the relative error of the added mass is only 1.9%and that of damping coefficient only 2.5%.That means although the paper adopts the filtering method to guarantee the convergence of the hydrodynamic forces of the heaving moment,it influences the precision of hydrodynamic forces weakly.If a reasonable filtering coefficient is chosen,it is reasonable to adopt the filtering method to resolve the heaving problems of large flattering structure.The main rule of choosing a reasonable filtering coefficient is selecting the magnitude which can have the most accurate added mass and damping coefficient on the basis of guaranteeing the result convergent.

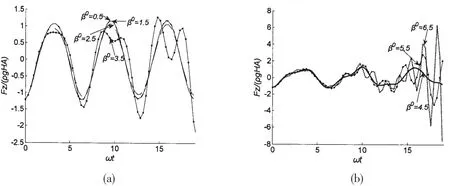
Fig.4 The hydrodynamic forces of small-amplitude heaving motion(ω=0.8,A/H=0.05)

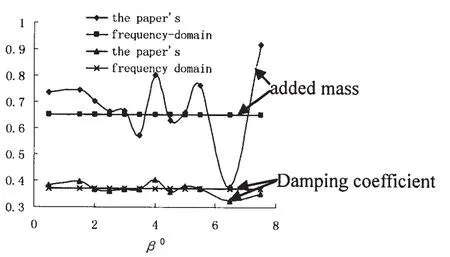
Fig.5 Added mass and damping coefficient

2.2 large-amplitude motion

For large-amplitude motion,the paper still takes the conical structure with α=45°as an example to analyze the influence of the filtering coefficient β0on the convergence property.Figs.6-8 give the hydrodynamic force of heaving motion with amplitude A/H=0.2,0.5,0.7 respectively.For all these three amplitudes,the hydrodynamic force is convergent when β0is less than 2.5,otherwise divergent.As a result,the optimum valueof the filtering coefficient β0nearly has nothing to do with heaving amplitude A/H.

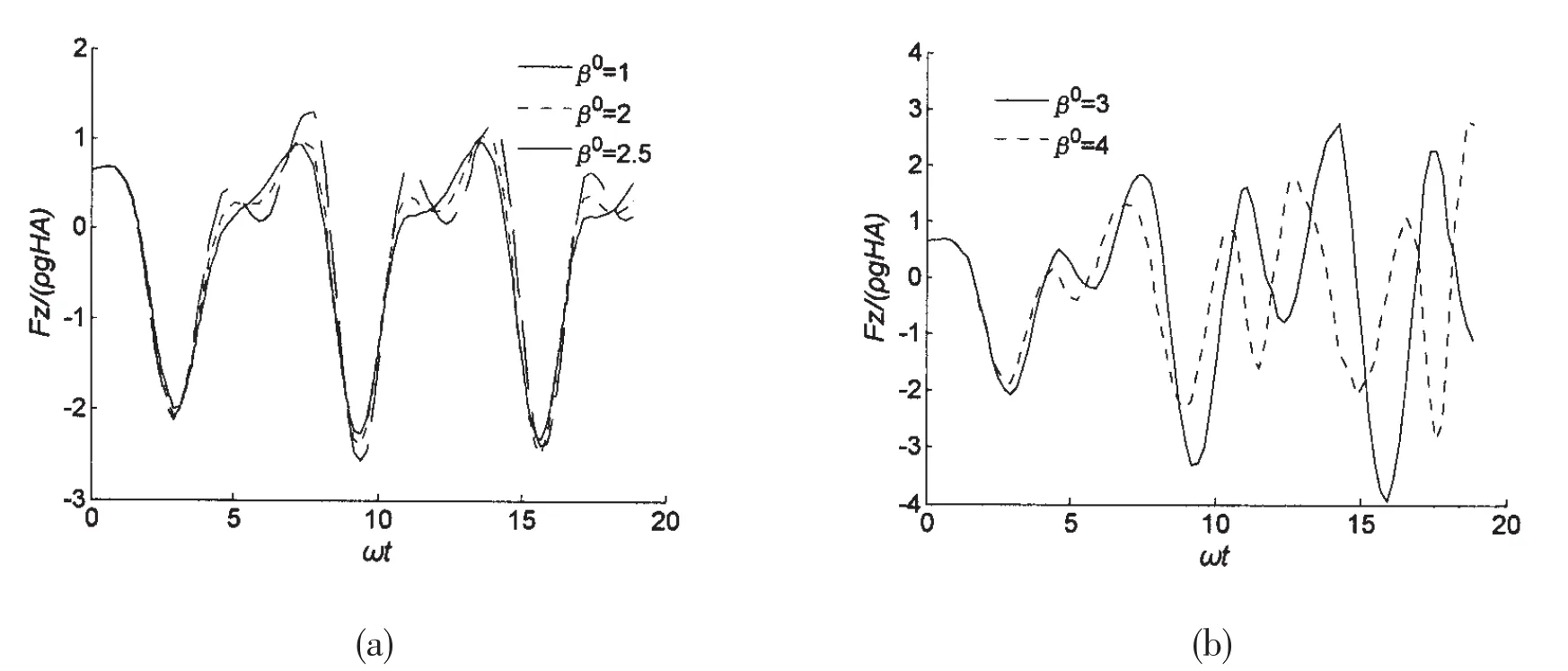
Fig.6 The hydrodynamic forces of large-amplitude heaving motion(ω=0.8,A/H=0.2)

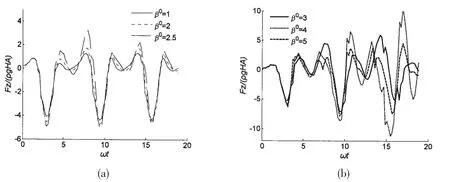
Fig.7 The hydrodynamic forces of large-amplitude heaving motion(ω ■ H /g =0.8,A/H=0.5)

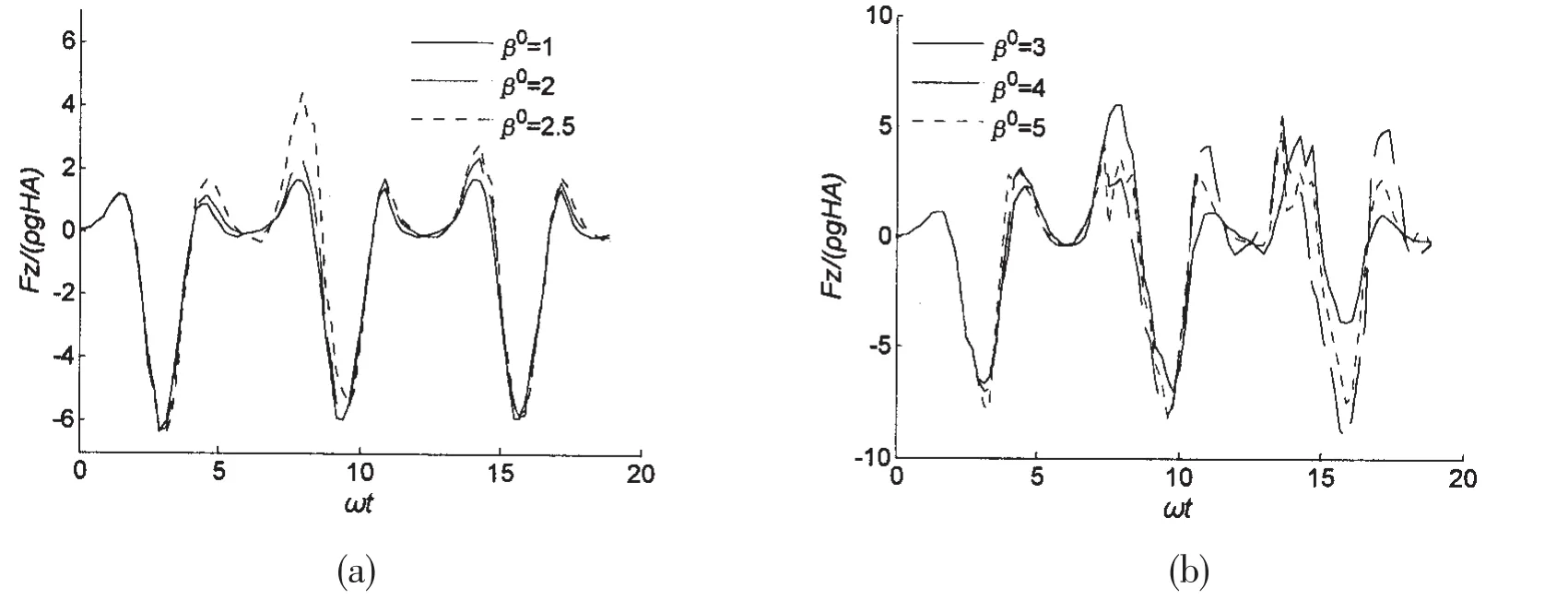
Fig.8 Fig.8 The hydrodynamic forces of large-amplitude heaving motion(ω=0.8,A/H=0.7)

2.3 The influence of ω and α

From above analysis,it founds that the amplitude ofnearly has nothing to do with motion amplitude A/H.In this section,the heaving frequency ω and the deadrise angle α of the cone are changed to analyze the convergence property which is given in Fig.9.This figure shows thatdecreases along with heaving frequency ω greatly when ω is less than 4 and this change becomes gentle when ω is more than 4.mainly becomes larger when α decreases.This change has a little difference when ω is less than 2.

Fig.9 Change ofalong α

3 Conclusions

The filtering scheme put forward by this paper is effective which can make the hydrodynamic force on those structures with oblique boundaries convergent and the added mass and the damping coefficient approaching that by frequency domain Green function method if an optimum filtering coefficientis chosen.Thus,convergence property and precision of hydrodynamic coefficients are both rules judging an optimum valueof the filtering coefficientnearly has nothing to do with heaving amplitude A/H,but is influenced by heaving frequency ω and the deadrise angle α.

[1]Liu Yingzhong.Theory of ship wave making resistance[M].Beijing:National Defense Industry Press,2003.(in Chinese)

[2]Chen J P,Zhu D X,Liu X D.A research on numerical prediction method for wave-making resistance and its application to container ship hull form optimization[J].Journal of Hydrodynamics,Ser.A.,2006,21(1):113-121.(in Chinese)

[3]Sun S L,Wu G X.Oblique water entry of a cone by a fully three dimensional nonlinear method[J].Journal of Fluids and Structures,2013,42:313-332.

[4]Wu G X,Sun S L.Similarity solution for oblique water entry of an expanding paraboloid[J].Journal of Fluid Mechanics,2014,745:398-408.

[5]Huang D B.Approximation of time-domain free surface function and its partial derivatives[J].Shipbuilding of China,1992,4:16-25.

[6]Chang J M,Qiu W,Peng H.On the evaluation of time-domain Green function[J].Ocean Engineering,2007,34:962-969.

[7]Lin W M,Yue D K P.Numerical solutions for large amplitude ship motions in the time domain[M].In:Proceedings of the 18th Symposium on Naval Hydrodynamics.National Academy Press,Washington,DC.,1990:41-66.

[8]Sen D.Time-domain computation of large amplitude 3D ship motions with forward speed[J].Ocean Engineering,2002,29(8):973-1002.

[9]Singh S P,Sen D.A comparative linear and nonlinear ship motion study using 3-D time domain methods[J].Ocean Engineering,2007,34:1863-1881.

[10]Dong G H,Sun L,Zong Z,Zhao Y P.Numerical analysis of the forces exerted on offshore structures by ship waves[J].O-cean Engineering,2009,36:468-476.

[11]Chen X B,Wu G X.On singular and highly oscillatory properties of the Green function for ship motions[J].J Fluid Mech.,2001,445:77-91.

[12]Newman J N.The approximation of free-surface Green functions[C].Manuscript for Fritz Ursel Retirement Meeting,1990:29-30.

[13]Wang R S.Numerical approximation of three-dimensional free-surface Green function and its partial derivatives(frequency-domain infinite water depth)[J].Journal of Hydrodynamics,Ser.A,1992,7(3).

[14]Chen X B,Duan W Y.Cappillary-gravity waves due to an impulsive disturbance[C]//Proc.18th Intl workshop on Water Waves and Floating Bodies.Carry-Le-Rouet(France),2003.

[15]Chen X B,Duan W Y,Lu D Q.Gravity-waves with effect of surface tension and fluid viscosity[C]//Proc.21th Intl workshop on Water Waves and Floating Bodies.Carry-Le-Rouet(France),2006.

[16]Abramowitz M,Stegun I A.Handbook of Mathematical Functions with Formulas,Graphs and Mathematical Tables[K].Government Printing Office,Washington,and Dover,New York,1964.