QI Hao,Elkin Vumar

(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: Given a graph G=(V,E)and mutually disjoint nonempty subsets A1,A2,...,Ar of V,we say that G is spanning cyclable with respect to A1,A2,···,Ar if there exist mutually disjoint cycles C1,C2,···,Cr such that Ai? V(Ci)for i=1,2,···,r and C1∪C2∪···∪Cr spans G.And G is r-spanning-cyclable if G is spanning cyclable with respect to A1,A2,...,Ar for every such mutually disjoint nonempty subsets of V.Moreover,we say that G is r-spanning-cyclable of order t if G is spanning cyclable with respect to A1,A2,···,Ar for any r nonempty mutually disjoint subsets A1,A2,···,Ar of V such that|A1∪A2∪···∪Ar|≤ t.In this paper we prove if G is a graph of order n ≥ 3r+1(r≥ 1)and has at least+k+r?2 edges for 3≤k≤n?r+1,then G is r-spanning-cyclabe of order k+r?3.Our result extends the result obtained by Cheng et al.in[1]for r=2.

Key words:Hamiltonian graph;cyclability;spanning cyclability

0 Introduction

For the graph definitions and notation we follow[2].LetG=(V,E)be an undirected connected graph.A Hamilton cycle(path)of a graphGis a spanning cycle(spanning path)of it,i.e.,a cycle(path)that contains every vertex ofG.A graphGis hamiltonian(traceable)if it has a Hamilton cycle(path),andGis Hamilton-connected if there exists a Hamilton path between any two distinct vertices ofG.

Hamiltonicity is one of the most intensively studied topics in graph theory.In recent decades,some variations of Hamiltonian problem have been considered and many papers have been published concerning to the specified variations[3][4].For example,the so called k-ordered Hamiltonian problem is the one strengthening the condition to include a prescribedkvertices in a specific order[5][6][7],and the spanning cyclability of a graph is another one to find the condition for the graph to be spanned by several mutually disjoint cycles such that each of them must contain a prescribed set of vertices[1][8].For our purpose here,we present some definitions and terminology on spanning cyclability of graphs which are introduced in[1]and[8].

Given a graphG=(V,E)and mutually disjoint nonempty subsetsA1,A2,...,ArofV,we say thatGis cyclable with respect toA1,A2,...,Arif there exist mutually disjoint cyclesC1,C2,...,Crsuch thatAi?Cifor 1≤i≤r.If,in addition,C1,C2,...,CrspansG,thenGis spanning cyclable with respect toA1,A2,...,Ar.Gis r-spanning-cyclable ifGis spanning cyclable with respect toA1,A2,...,Arfor every such mutually disjoint nonempty subsets ofV.We say thatGis r-cyclable of order t ifGis cyclable with respect toA1,A2,...,Arfor anyrnonempty mutually disjoint subsetsA1,A2,...,ArofVsuch that|A1∪A2∪ ···∪Ar|≤t.Moreover,Gis r-spanning-cyclable of order t ifGis spanning cyclable with respect toA1,A2,...,Arfor anyrnonempty mutually disjoint subsetsA1,A2,...,ArofVsuch that|A1∪A2∪···∪Ar|≤t.The spanningr-cyclability ofGis the maximum integertsuch thatGis spanningr-cyclable of orderkfork=r,r+1,...,t,but not spanningr-cyclable of ordert+1.

The problem ofrcycles spanningGsuch that each cycle contains the prescribed vertices has been studied recently by some authors in[1]and[8].In[8],the authors study the spanning cyclability properties of then-dimensional hypercubeQn.It is shown thatQnis spanning 2-cyclable of ordern?1 forn≥3 andQnis spanningk-cyclable of orderkforn≥2 andk≤n?1.Moreover,it is shown that the spanning 2-cyclability ofQnisn?1 forn≥3.

In[1]the authors consider the cyclability of general graphs.They first give three types of degree conditions for a graph to ber-spanning-equi-cyclable(for the definition ofr-spanning-equi-cyclable).And then they give some sufficient conditions for extremal types,which we list in below out of special interest.

Theorem 1[1]IfGis a graph onnvertices withn≥ 7 and has at least+3 edges,thenGis 2-spanningcyclable of order 2.

Theorem 2[1]IfGis a graph onnvertices withn≥ 7 and has at least+kedges for 4≤k≤n?1,thenGis 2-spanning-cyclable of orderk?1.

In this note we extend the above theorems by promoting 2-spanning cyclable tor-spanning cyclable for

1 Main results

We list our main result as two theorems here since the proofs are different.

Theorem 3IfGis a graph onnvertices withn≥ 3r+1(r≥ 1)and has at least+r+1 edges,thenGisr-spanning-cyclable of orderr.

Theorem 4IfGis a graph onnvertices withn≥ 3r+1(r≥ 1)and has at least+k+r?2 edges for 4≤k≤n?r+1,thenGisr-spanning-cyclable of orderk+r?3.

Combining the above two theorems,we have

Theorem 5IfGis a graph onnvertices withn≥ 3r+1(r≥ 1)and has at leastedges for 3≤k≤n?r+1,thenGisr-spanning-cyclable of orderk+r?3.

Before staring our proofs we list two useful results.

Theorem 6[9]IfGis a graph of ordernand has at least+2 edges,thenGis Hamiltonian.

Lemma 1[1]LetAbe a vertex subset ofGsuch that 2≤|A|≤|V(G)|?1,and letCbe a cycle of minimum length inGamong cycles containingA.If|V(C)|≥ 4 and|V(C)|>|A|,then|E(C)|≤?(|V(C|?|A|).

Proof of Theorem 3LetA1,A2,...,Arbe mutually disjoint nonempty subsets ofV(G)andAi={xi},w.l.o.g.assumed(xi)≤d(xi+1)for 1≤i≤r?1.SetB1=A1∪A2∪···∪Ar={x1,x2,...,xr}andB2=V(G)B1.

We first note that the condition|E(G)|≥+r+1 impliesd(v)≥r+1 for anyv∈V(G),since otherwise|E(G)|≤?(n?1?r)=+r,a contradiction.

Whenr=1,the theorem follows by Theorem 6.Letr≥2,and we prove the theorem by induction onr.

By Theorom 1,the conclusion follows whenr=2.

Now letr≥3,and assume that the conclusion follows whenr?1,that is to say ifGis a graph onnvertices withn≥ 3r?2 and has at least+redges,thenGis(r?1)-spanning-cyclable of orderr?1.

Case 1d(xi)≤n?3 fori=1,2,...,r.

Assumed(x1)=k,thenk≥r+1.LetNB2(x1)={y1,y2,...,ym},sok?(r?1)≤m≤k.

Ifyiyjfor anythen sincewe have

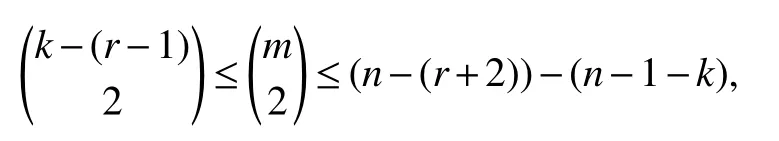
By the induction hypothesisZis(r?1)-spanning-cyclable of orderr?1,so there are disjoint cyclesC2,C3,...,Crsuch thatAi?V(Ci)fori=2,3,...,r,andC2∪C3∪···∪CrspansZ.Then there are disjoint cyclesC1,C2,C3,...,Crsuch thatAi?V(Ci)fori=1,2,...,r,andC1∪C2∪C3∪···∪CrspansG.AndGisr-spanning-cyclable of orderr.

Case 2d(x1)=n?2 and there exists

subcase 2.1There is anxjsuch that

Clearlyd(xj)≤n?2.SetB2={y1,y2,...,yn?r}andd(yi)≤d(yi+1)for 1≤i≤n?r?1.Note thatB2?N(x1),we consider the degree ofy1.

subcase 2.1.1d(y1)=n?1.

We have thatd(yj)=n?1 fori=1,2,...,n?r.TakeClearly,C1,C2,...,Crare disjoint cycles such thatAi?V(Ci)fori=1,2,...,r,andC1∪C2∪C3∪···∪CrspansG.HenceGisr-spanning-cyclable of orderr.

subcase 2.1.2d(y1)≤n?2.

Sinced(y1)≥r+1,there existsy1ys∈E(G)for some.Becaused(x1)=n?2,d(y1)≤n?2 andd(ys)≤n?1,we have

Now this subcase reduces to Case 1.

subcase 2.2x1xi∈E(G)fori=2,3,...,r.

Sinced(x1)=n? 2,there exists a vertexvinB2but not inandd(yi)≤d(yi+1)for 1≤i≤n?r?2.We also consider the degree ofy1.

subcase 2.2.1d(y1)=n?1.

In this Subcase,similar to that in Subcase 2.1.1,we take

subcase 2.2.2d(y1)≤n?2.

We know thatd(y j)≥r+2 forj=1,2,...,n?r?1,otherwise,there existsd(y j0)=r+1 for somej0,then+r,a contradiction.Thusy1has at least two neighbors inB2,and this fact together withd(x1)=n?2 imply thatx1andy1have a common neighbor,say,y2inB2.SetandSinced(x1)=n?2,d(y1)≤n?2 andd(y2)≤n?1,we have

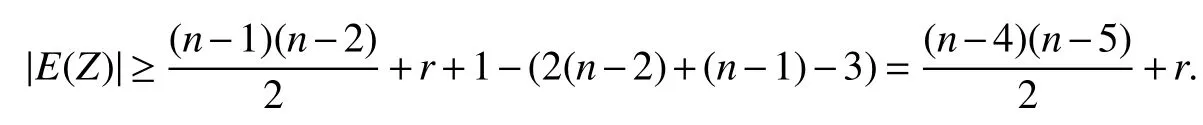
Now this subcase reduces to Case 1.

Case 3d(x1)≥n?2 andd(xi)=n?1 fori=2,3,...,r.

Letybe a vertex of minimum degree ofGinB2.

Ifd(y)=n?1 andd(x1)=n?1,thenGKn,we are done.

Ifd(y)=n?1 andd(x1)=n?2,thenGwould have degree sequence(n?2,n?1,···,n?1,n?1),and there exists no any graph with such degree sequence.

Now we haver+1≤d(y)≤n?2.

subcase 3.1d(y)=n?2.

Ifd(w)=n?1 for anyw∈NB2(y),then we can find the needed cycles in Subcase 2.2.1.

Ifd(w)≤n?2 for somew∈NB2(y),then seandZ=G?V(C1).Sinced(x2)=n?1,d(y)=n?2 andd(w)≤n?2,we have

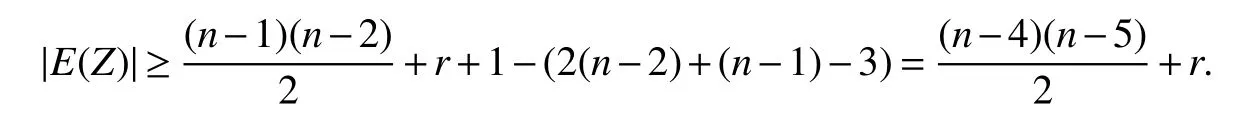
Now this subcase reduces to Case 1.

subcase 3.2d(y)≤n?3.

Sinced(y)≥r+1,there existsw∈B2such thatwy∈E(G).SetC1=x2ywx2andZ=G?V(C1).Sinced(x2)=n?1,d(y)≤n?3 andd(w)≤n?1,we have

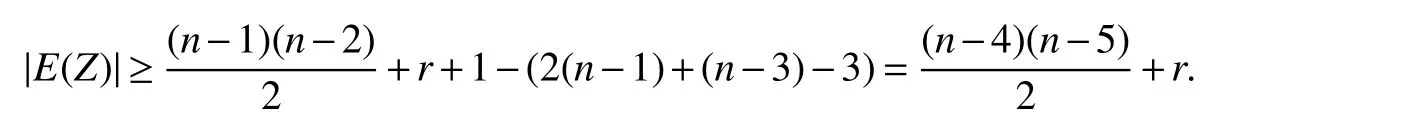
Now this subcase reduces to Case 1.

Proof of Theorem 4LetA1,A2,...,Arbe mutually disjoint nonempty subsets ofV(G)and|Ai|=ai(i=1,2,...,r)such that

Whenr=1,the theorem follows by Theorem 6.Letr≥2,and we prove the theorem by induction onr.

By Theorom 1,the conclusion follows whenr=2.

Now letr≥3,and assume that the conclusion follows whenr?1,i.e.,ifGis a graph onnvertices withn≥3r?2 and has at leastedges,thenGis(r?1)-spanning-cyclable of orderk+r?4 for 4≤k≤n?r+2.

First,setH=G?{A1∪A2∪···∪Ar?1}and we have

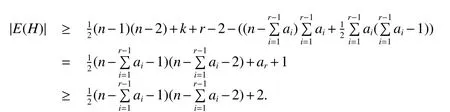
By Theorem 6His Hamiltonian.LetC1be a cycle of minimum length among cycles inHcontainingAr.Letc=|V(C1)|andZ=G?V(C1).We distinguish the following cases.

Case 1c=ar.

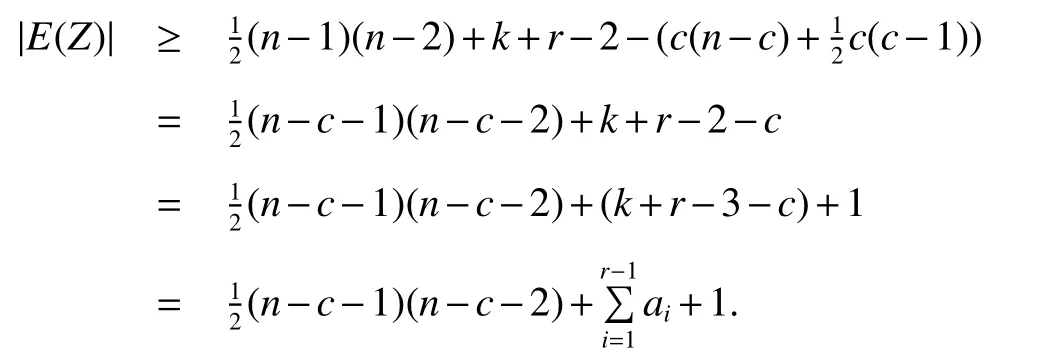
By the induction hypothesisZis(r?1)-spanning-cyclable of orderso there are disjoint cyclesC2,C3,...,Crsuch thatfori=2,3,...,randHence there are disjoint cyclesC1,C2,C3,...,Crsuch that|A1∪A2∪A3∪···∪Ar|≤k+r?3,Ai?V(Ci)fori=1,2,...,randC1∪C2∪C3∪···∪CrspansG,andGisr-spanning-cyclable of orderk+r?3.

Case 2c>ar.

subcase 2.1c≥4.

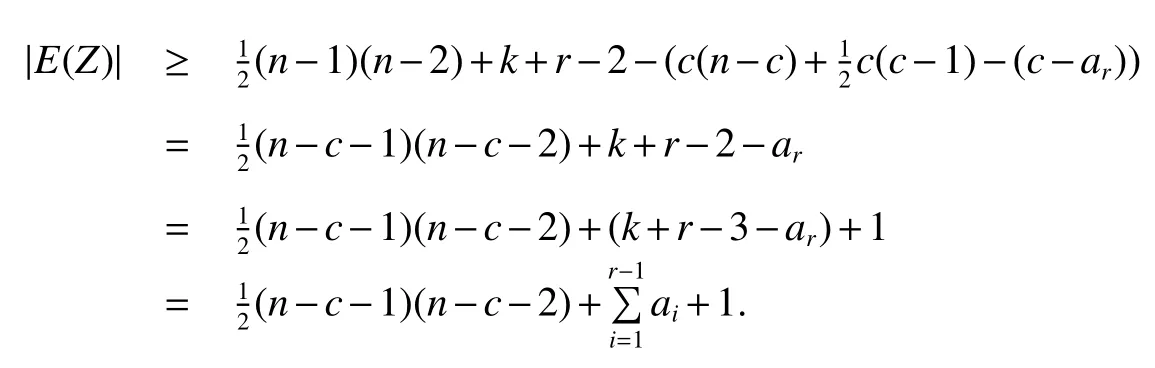
Now this subcase reduces to Case 1.

subcase 2.2c=3.

Ifar=1,we havea1=a2= ···=ar=1,now this subcase follows by Theorem 3.

Ifar=2,thenk+r?3≤2rand thus 4≤k≤r+3.LetAi=fori=1,2,...,r?1,perhapsdoes not exist.

subcase 2.2.1min{d(p),d(q)}≤n?2.

In this event,we have

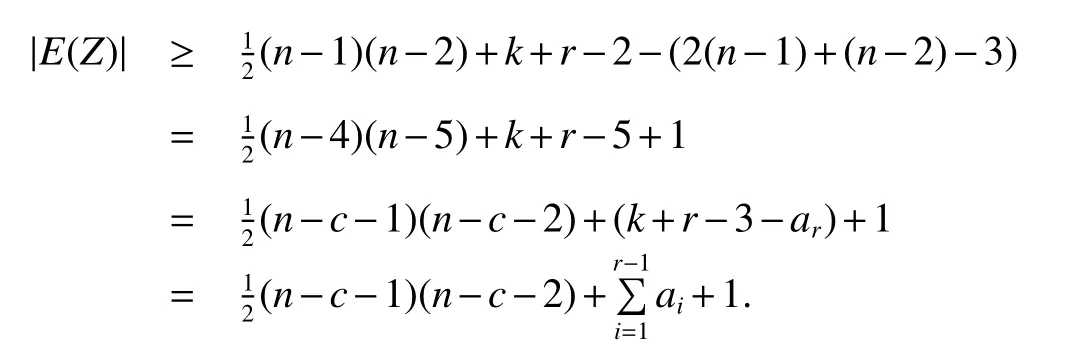
Now this subcase reduces to Case 1.

subcase 2.2.2d(p)=d(q)=n?1.

If every vertex ofHhas degreen?1 inG,then the claim trivially holds.Otherwise there must be a vertexwinHwith degreed(w)≤n?2.RedefineC1=pwqpandZ=G?V(C1)then similar to that in Subcase 2.2.1 we can find the desired cycles.