Lanmei Wang,Zhihai Chen,Guibao Wang,and Xuan Rao

1.School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China;

2.National Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China;

3.Department of Mathematics,San Francisco State University,San Francisco CA 94132,USA

Estimating DOA and polarization with spatially spread loop and dipole pair array

Lanmei Wang1,3,*,Zhihai Chen1,Guibao Wang2,3,and Xuan Rao2

1.School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China;

2.National Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China;

3.Department of Mathematics,San Francisco State University,San Francisco CA 94132,USA

The nonuniform L-shaped spatially spread loop and dipole(SSLD)array whose inter-element spacing is greater than half a wavelength is studied.A joint parameter estimation algorithm of direction of arrival(DOA),frequency and polarization is presented for plane-wave signals.The direct sampling and the corresponding delayed sampling data are used to construct the data correlation matrix.On the basis of the subspace theory and the least square method,the frequency and the steering vector of the whole array are obtained.According to the relationship of the array manifold vector between electric dipoles and magnetic loops, the polarization parameters are given.The unambiguous phase estimates are acquired by applying virtual baseline array transformation to the spatial steering vectors,and they are used as coarse references to disambiguate the cyclic phase ambiguities in phase differences between two adjacent array elements on the array, then the high accuracy DOA estimates are obtained.Closed-form solutions for each parameter are obtained.This method has advantages of lower calculation complexity and no parameter matching.The experiment results verify the effectiveness and feasibility of the presented algorithm.

array signal processing,L-shaped array,direction of arrival(DOA),polarization,subspace theory.

1.Introduction

Array signal processing technique has played a primary role in many applications involving radar,sonar and communications.However,estimating the direction of arrival (DOA)is of great interest to communication and radar systems[1–8].

Signal subspace based algorithms such as MUSIC and ESPRIT are known to have high resolution.The MUSIC algorithm[9–10]is suitable for various array architectures,which has wide applications in the feld of engineering.It performs a four-or two-dimensional spectrum peak search for polarization and DOA estimation,and its shortcomings are no closed-form solution and large computing capacity.The ESPRIT algorithm is used to the array with a rotational invariance structure and is computationally effcient.The L-shaped array has good performance with fewer array element numbers in signal processing, and scholars have studied the ESPRIT algorithm based on uniform L-shaped arrays[11–17].

The electromagnetic vector sensor array is a new type of array due to its polarization diversity[9,18,19].Vector sensors are already commercially available,for example, from Flam and Russell,Inc.,Horsham,PA[20,21],and from EMC Baden,Inc.,Baden,Switzerland.In contrast to co-located dipoles and loops array[5,7,22,23],the spatially spread loop and dipole(SSLD)array has great practical value,in reducing mutual coupling,simplifying the antennas hardware,and sparsely extending the spatial aperture to refne the direction-fnding accuracy by orders of magnitude[22,24].Meanwhile,the inter-element spacing with greater than half a wavelength leads to cyclically ambiguousangle estimates.The ambiguitymeans that several false signals are estimated for only one signal source,i.e., the ambiguity means that the steer-vectors made from the real DOA is similar to the ones from the false DOA[25–28].

In this paper,the nonuniform L-shaped SSLD array whose inter-element spacing is greater than half a wavelength is studied.We propose a subspace-based direction fnding(DF)approach which overcomes the ambiguity of DOA estimation and improves the resolution capability of L-shaped arrays by extending the aperture size.By applying dot divide operation to array steering vectors and using the least square method,the signal parameters areestimated.The method only needs one time eigenvalue decomposition without parameter matching.The main feature of our proposed method is that it combines the low computation and super resolution capability.Numerical examples show that the proposed DF method achieves a better performance.

2.Problem formulation

The receiving array is a nonuniform L-shaped array which consists of M?1 SSLD pairs and one collocated loop and dipole(COLD)pair in the x?y plane.As shown in Fig.1, the COLD pair oriented along the z axis of the Cartesian coordinate can measure the electric-feld and magneticfeld z-component[7,22,23].The COLD pair is located at the origin of the Cartesian coordinate.The x-axis and yaxis sub-arrays are respectively composed of M?1dipoles and M?1loops.The inter-element spacing of the two subarrays are D,D+d,...,D+(M?2)d,with D?0.5λminand d＜0.5λmin,as shown in Fig.2.

Fig.1 COLD pair geormetry

Fig.2 Nonuniform L-shaped array geometry

Assume that K(K≤M?3)uncorrelated narrowband sources impinge on the receiving array from far-feld.For the kth source,θk∈[0,π/2]is the signal’s elevation angle measured from the positive z-axis,?k∈[0,2π]is the signal’s azimuth angle measured from the positive x-axis,fkis the frequency,where k=1,2,...,K.

The two sub-array steering vectors respectively consisting of M dipoles and M loops can be expressed as A1and A2:

where

3.Parameter estimation algorithm

A temporal invariance is formed by utilizing two timedelayed sets of data collected from the nonuniform L-shaped SSLD pairs array;that is,the kth signal impinging upon the array would contribute toward two 2×M data sets

With a total of impinging signals at the array,the entire 4M×N data set is

where

withX(t)is the received signal,B1and B2are the 2M×K steering vector matrix of K incident signals,S(t)is the incident signal and N(t)is assumed to be the zero mean and σ2variance,complex Gaussian random processe that is statistically independent of each other.Note that the invariance exp(j2πfkΔT)does not depend on either the DOA or the polarization state,but only on the signal frequency and the time delay ΔT.

The correlation matrix of overall data X(t)is

where E[?]symbolizes the statistical mean,(?)Hdenotes the complex conjugate transpose,σ2indicates the white noise power and Rs= E[S(t)SH(t)]represents the source covariance matrix.Let Esbe the 4M×K matrix composed of K eigenvectors corresponding to K largest eigenvalues of Rxand let Endenote the 4M×(4M?K) matrix composed of the remaining 4 M?K eigenvectors of Rx.According to the subspace theory,the signal subspace can be expressed explicitly as

Equation(13)implies that the estimation of Φ is a matrix whose diagonal elements are composed of K largest eigenvalues of matrixand the full-rank matrixis composed of K eigenvectors of matrixThe estimation of B1can be written as

The estimation of frequency can be obtained from Φ.

Polarization parameters can be got from

where./denotes the dot division which is the division of the corresponding elements of two vectors.

Let

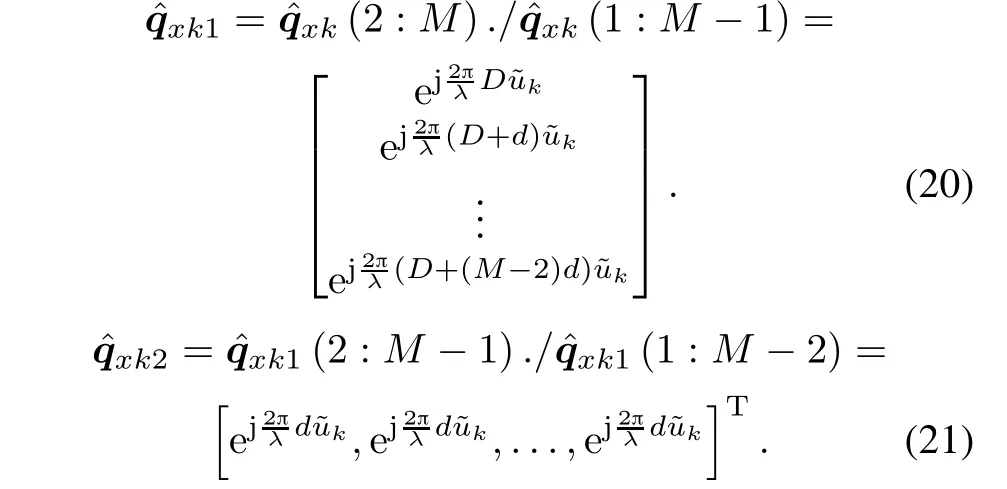
According to(4)and(5),the phase angles of qxk(M) and qyk(M)can be expressed as

where

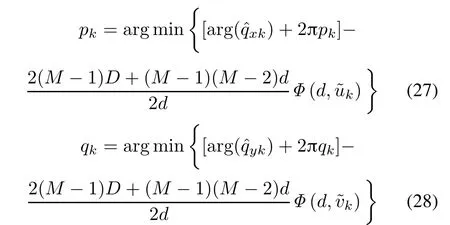
with

From(23),(24),(25)and(26),the accurate estimations of direction cosine are obtained:

From(31)and(32),DOA parameters can be obtained as follows:

4.Simulation results

To illustrate the noise performance,some simulations are conducted to evaluate the performances on DOA/frequency/polarization estimation by the proposed method.Two uncorrelated equal-powered signals with parameters(θ1,?1,γ1,η1)=(70°,30°,40°,80°), (θ2,?2,γ2,η2)= (20°,40°,45°,60°)and(f1,f2)= (11M,12M)Hz,impinging upon two arrays all with 2M=12 dipole and loop sensors.The inter-element spacing variables are D=2λ,d=0.4λ and the sampling frequency is fs=40 MHz.Five hundred snapshots are used in each of the 200 independent Monte Carlo simulation experiments.

The circular curve and the star curve plot the standard deviation of azimuth and elevation,respectively estimated by the uniform array ESPRIT method and the proposed nonuniform array method,at different signal-to-noise ratio (SNR)levels,as shown in Fig.3 and Fig.4.

Fig.3 Standard deviation of azimuth versus SNR

Fig.4 Standard deviation of elevation versus SNR

In the SNR range(namely,at or above 0 dB)DOA estimation based on the nonuniform L array model has better performance than that based on the uniform L array model.The estimation precision at 0 dB based on the proposed nonuniform array model has been improved by larger than 0.86°for azimuth angle,0.35°for elevation angle,compared with that of the uniform L array ESPRIT method.The enhanced performance is rooted in the sparse embattle of L-shaped arrays.

The circular curve and the star curve plot the standard deviation of auxiliary polarization angle(APA)and polarization phase difference(PPD),respectively estimated by the uniform array ESPRIT method and the proposed nonuniform array method,at different SNR levels,as shown in Fig.5 and Fig.6.The performance of the two methods is nearly the same.PPD and APA are obtained according to the relationship of dipole and loop sub-array steering vectors.

Fig.5 Standard deviation of APA versus SNR

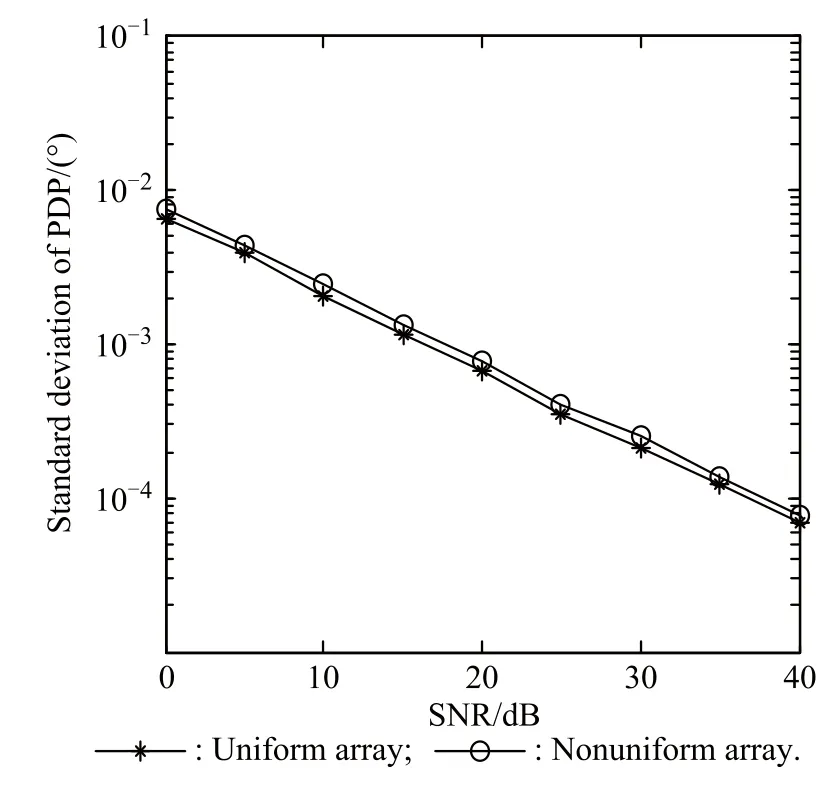
Fig.6 Standard deviation of PDP versus SNR

5.Conclusions

A closed-form solution for estimating DOA/frequency/polarization,based on the nonuniform L-shaped array consisting of SSLD pairs is derived in this paper.According to the time invariance and the subspace theory,the steering vector of the whole array and signal frequency are obtained.Polarization parameters are given according to the array manifold vector relationship between electric dipoles and magnetic loops.The unambiguous phase estimates are acquired by applying dot divide operation to the spatial steering vectors,and they are used as coarse references to disambiguate the cyclic phase ambiguities in phase difference of spatial steering vectors.The high accuracy DOA estimates are obtained.The proposed nonuniform L-shaped sparse array is very important in engineering.

[1]X.Yuan.Spatially spread dipole/loop quads/quints:for direction fnding and polarization estimation.IEEE Antennas and Wireless Propagation,2013,12(3):1081–1084.

[2]K.Yang,Z.Q.Zhao,W.Yang,et al.Direction of arrival estimation on cylindrical conformal array using RARE.Journal of Systems Engineering and Electronics,2011,22(5):767–772.

[3]M.Diao,C.L.An.Direction fnding of coexisted independent and coherent signals using electromagnetic vector sensor.Journal of Systems Engineering and Electronics,2012, 23(4):481–487.

[4]N.Kannan,N.Ravishanker.High resolution estimation for sub-Gaussian stable signals in a linear array model.IET Signal Processing,2007,1(1):35–42.

[5]X.Yuan,K.T.Wong,Z.Xu,et al.Various compositions to form a triad of collocated dipoles/loops,for direction fnding and polarization estimation.IEEE Sensors Journal,2012, 12(6):1763–1771.

[6]J.Liu,Z.Liu,Q.Liu.Direction and polarization estimation for coherent sources using vector sensors.Journal of Systems Engineering and Electronics,2013,24(4):600–605.

[7]J.Li,P.Stoica,D.Zheng.Effcient direction and polarization estimation with a COLD array.IEEE Trans.on Antennas and Propagation,1996,44(4):539–547.

[8]C.F.Liu,J.Yang,F.S.Wang.Joint TDOA and AOA location algorithm.Journal of Systems Engineering and Electronics,2013,24(2):183–188.

[9]K.T.Wong,M.D.Zoltowski.Self-initiating MUSIC direction fnding and polarization estimation in spatio-polarizational beamspace.IEEE Trans.on Antennas and Propagation,2000, 48(8):1235–1245

[10]K.T.Wong,M.D.Zoltowski.Root-music-based azimuthelevation angle-of-arrival estimation with uniformly spaced but arbitrarily oriented velocity hydrophones.IEEE Trans.on Signal Processing,1999,47(12):3250–3260.

[11]N.Tayem,H.M.Kwon.L-shaped 2-dimensional arrival angle estimation with propagator method.IEEE Trans.on Antennas and Propagation,2005,53(5):1622–1630.

[12]J.F.Gu,W.P.Zhu,M.N.S.Swamy.Performance analysis of 2-D DOA estimation via L-shaped array.Proc.of the 25th IEEE Canadian Conference on Electrical and Computer Engineering,2012:1–4.

[13]G.M.Wang,J.M.Xin,N.N.Zheng,et al.New method for joint elevation and azimuth direction estimation with L-shaped array.Proc.of the 10th IEEE International Conference on Signal Processing,2010:336–339.

[14]J.L.Liang,D.Liu.Joint elevation and azimuth direction fnding using L-shaped array.IEEE Trans.on Antennas and Propagation,2010,58(6):2136–2141.

[15]Q.Cheng,Y.M.Zhao,J.Yang.Improvement of2-D DOA estimation based on L-shaped array.Proc.of the 10th IEEE International Symposium on Antennas,Propagation&EM Theory, 2012:1233–1236.

[16]P.Palanisamy,C.Kishore.2-D DOA estimation of quasistationary signals based on Khatri-Rao subspace approach.Proc.of the IEEE International Conference on Recent Trends in Information Technology,2011:798–803.

[17]X.Q.Hu,Y.L.Wang,H.Chen.2-dimensional arrival angle estimation and self-calibration algorithm for L-shaped array in the presence of mutual coupling.Proc.of the International Conference on Intelligent Computation Technology and Automation,2011:319–322.

[18]K.T.Wong,M.D.Zoltowsk.Closed-form direction fnding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations.IEEE Trans.on Antennas and Propagation,2000,48(5):671–681.

[19]J.Li,R.T.Compton.Two-dimensional angle and polarization estimation using the ESPRIT algorithm.IEEE Trans.on Antennas and Propagation,1992,40(5):550–555.

[20]D.J.Farina.Superresolution compact array radiolocation technology(Super CART)project.Horsham:Flam&Russell Tech, 1990.

[21]G.F.Hatke.Performance analysis of the super CART antenna array.Cambridge:MIT Lincoln Laboratory,1992.

[22]X.Yuan,K.T.Wong,K.Agrawal.Polarization estimation with a dipole-dipole pair,a dipole-loop pair,or a loop-loop pair of various orientations.IEEE Trans.on Antennas and Propagation,2012,60(5):2442–2452.

[23]L.M.Wang,G.B.Wang,Z.H.Chen.Joint DOA-polarization estimation based on uniform concentric circular array.Journal of Electromagnetic Waves and Applications,2013,27(13): 1702–1714.

[24]K.T.Wong,X.Yuan.Vector cross-product direction-fndingwith an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops.IEEE Trans.on Signal Processing,2011,59(1):160–171.

[25]P.Christos,M.Athanssios.Study of ambiguities of linear arrays.Proc.of the IEEE International Conference on Acoustics, Speech,and Signal Processing,1994:549–552.

[26]Z.Y.He,Z.Q.Zhao,Z.P.Nie,et al.Resolving manifold ambiguities for sparse array using planar substrates.IEEE Trans.on Antennas and Propagation,2012,60(5):2558–2562.

[27]L.Q.Zhang,H.D.Quan.Study on the direction fnding ambiguities performance of non-uniform linear antenna array.Proc.of the International Conference on Instrumentation, Measurement,Computer,Communication and Control,2011: 789–791.

[28]H.Gazzah,K.Abed-Meraim.Optimum ambiguity-free directional and omnidirectional planar antenna arrays for DOA estimation.IEEE Trans.on Signal Processing,2009,57(10): 3942–3953.

Biographies

Lanmei Wang was born in 1975.She received her M.S.degree in radio physics in 2003 and Ph.D.degree in information engineering in 2005, both from Xidian University,Xi’an,China.Her research interests include polarization sensitive array signal processing,and the application of compressed sensing and frame theory in array signal processing.

E-mail:lmwang@mail.xidian.edu.cn

Zhihai Chen was born in 1989.He is currently working toward his M.S.degree in radio physics at Xidian University,Xi’an,China.His research interests focus on parameter estimation of electromagnetic vector sensor array processing based on the hypercomplex algebra and geometric algebra.

E-mail:chenzhihai198968@163.com

Guibao Wang was born in 1977.He received his M.S.degree in computational mathematics in 2003.He had been worked as an engineer at a communication company for many years.Now he is a Ph.D.in the National Key Laboratory of Radar Signal Processing of Xidian University.His research interests focus on the polarization sensitive array signal processing.

E-mail:gbwang2008@gmail.com

Xuan Rao was born in 1977. He received his B.S.and M.S.degrees in signal processing from the School of Information Engineering,Nanchang University,Nanchang,China,in 1999 and 2005,respectively.He is currently a lecturer in the School of Information Engineering,Nanchang Hangkong University,China.And he is working toward his Ph.D.degree in the National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an,China.His current research interests include weak multiple-target detection,weak multipletarget tracking and maneuvering-target tracking.

E-mail:292408925@qq.com

10.1109/JSEE.2015.00007

Manuscript received December 06,2013.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61201295;61231017)and the Fundamental Research Funds for the Central Universities(K5051307017).