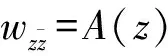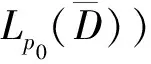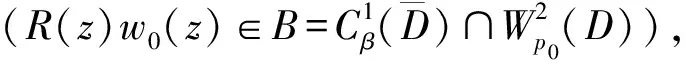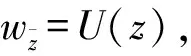The Discontinuous Mixed Problem for Elliptic Complex Equations of Second Order in Multiply Connected Domains
WEN Guo-chun
(LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China)
1 Formulation of Discontinuous Mixed Problem for Elliptic Complex Equa-tions of Second Order
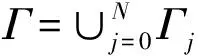
(1)
Suppose that the complex equation (1) satisfies the conditions, namely
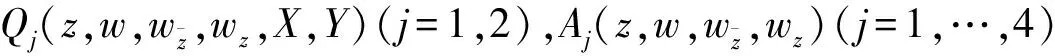
(2)
wherep0,p(2 3) The complex equation (1) satisfies the following uniform ellipticity condition, namely for any functionsw(z)∈C1(D) andXj,Yj∈C (j=1,2), the inequality (3) holds for almost every pointz∈D, whereqj(q1+q2≤q0<1,j=0,1,2) are all non-negative constants. We introduce the mixed boundary value problem for the second order complex equation (1) namely (4) (5) andK=(K1,K2) is called the index of Problem M. Moreover,λj(z),rj(z) (j=1,2),σ(z) satisfies the conditions (6) in whichα(1/2<α<1),kj(j=0,4,5) are non-negative constants,βjl+|γjl|<1,l=1,…,m,j=1,2; we require that the solutionw(z) possesses the property (7) in the neighborhood(?D) oftl(l=1,…,m), whereδ,τ(≤min(α,1-2/p0)) are small positive constants. In general, Problem M may not be solvable.Hence we consider the new modified well-posedness of Problem M as follows. ProblemNFind a continuously differentiable solutionw(z) inD*of the complex system (1) satisfying the modified boundary conditions (8) where (9) We must give the attention that the boundary circlesΓk(k=0,1,…,N) of the domainDare moved round the positive direct. Similarly to (1.7)-(1.12), Chapter V, [5], we see that are integers; and in whichSj(z) (j=1,2) are solutions of the modified Dirichlet problems with the above boundary conditions for analytic functions,θjk(j=1,2,k=1,…,N) are real constants, andκj=Kj-N0/2,j=1,2. In addition, forKj≥0 (j=1,2) the solutionw(z) is assumed to satisfy point conditions (10) whereal∈Γ0(l∈Jj, ifKj≥0) are distinct points, andbjl(l∈Jj,j=1,2) are all real constants satisfying the conditions (11) for a non-negative constantk6. First of all, we give the corresponding complex system of complex equations in the form (12) (13) (14) and point conditions (15) ProofLet the solutionw(z) of Problem N be substituted into the equation (12) and denote the equation in the form (16) hence we have (17) Noting thatw(z) satisfies the second formulas of boundary and point conditions (8) and (10), it is easy to see thatwz=Ψ'(z)+∏Tρsatisfies the complex equation (18) and the boundary condition (19) wheresis the arc length parameter ofΓ. (20) (21) in whichβ=min(α,1-2/p0),Mj=Mj(q1,p0,k0,β,D) (j=1,2) are non-negative constants, andk*=k3+k5+k6. ProofLet the solutionw(z) of Problem N be substituted into the equation (12) and boundary conditions (8),(10). It is easy to see thatw(z) satisfies the complex equation (12) and the second formulas in (8) and (10),i.e. (25) (26) whereβ,p0are stated as before, andMj=Mj(q1,p0,k0,β,D)(j=3,4) are non-negative constants, ∑j∈ J1[|sj|+|b1j|]≤q2S2w+(k1+k2+k4)S1w+k*≤q2S2w+k**S1w+k*, in whichk**=k1+k2+k4. Moreoverw(z) satisfies (17) and the second formulas in (8) and (10), and we can obtain the estimates (27) (28) whereMj=Mj(q1,p0,k0,β,D) (j=5,6) and M3[q2S2w+k**S1w]+k*(1+M3). In addition, from (16),(17) and the second formulas in (8) and (10), we know thatwzis a solution of the equation (29) satisfying the boundary condition (30) M7{[M4+k0M3(1+M5)][q2S2w+k**S1w+k*]+(1+k0M3M5)k*}, (31) whereM7=M7(q1,p0,k0,β,D). Thus the estimates M7{[M4+k0M3(1+M5)][q2S2w+k**S1w+k*]+(1+k0M3M5)k*}+M3k*+M5k**≤ M7[M4+k0M3(1+M5)+M3(1+M5)][q2S2w+k**S1w+k*]+[M7+M3M5(1+k0M7)]k*, (32) and M8{[M4+k0M3(1+M5)][q2S2w+k**S1w+k*]+(1+k0M5)}k*, (33) can be derived, whereM8=M8(q1,p0,k0,β,D).Combining (25)-(28) and (32), (33), we obtain S1w+S2w≤(M7+M8){[M4+k0M3(1+M5)+M3(1+M5)]× [q2S2w+k**S1w+k*]+k*}+M5(M3+k0M3M7+k0M8)]k*+M4k*≤ {M4+(M7+M8)[M4+k0M3(1+M5)+M3(1+M5)]}× [q2S2w+k**S1w+k*]+[M7+M8+M5(M3+k0M3M7+k0M8)]k*≤ {M4+(M7+M8)[M4+M3(1+k0)(1+M5)]}(q2+k**)× [S1w+S2w]+{M4+(M7+M8)[1+M4+M3(1+k0)(1+M5)]+ M5(M3+k0M3M7+k0M8)}k*≤M9k*=M9(k3+k5+k6). (34) Because we choose the sufficiently small positive constantsq2,k1,k2,k4in Condition C and (2),(3),(6), such that 1-{M4+(M7+M8)[M4+M3(1+k0)(1+M5)](q2+k**)}>1/2, and can select the positive constantM9=2{M4+(M7+M8)[1+M4+M3(1+k0)(1+M5)]+M5(M3+k0M3M7+k0M8)}. Thus the estimates (20) and (21)withM1=M2=M9are derived. (35) (36) Theorem3If Condition C and (35) hold, andq2,k1,k2,k4in (2),(3), (6) are small enough, then the solution [w(z),U(z),V(z)] of Problem N for (12) is unique. ProofDenote by [wj(z),Uj(z),Vj(z)](j=1,2) two solutions of Problem N for (1) and substitute them into (12),(8) and (10), we see that [w,U,V]=[w1(z)-w2(z),U1(z)-U2(z),V1(z)-V2(z)] is a solution of the following homogeneous boundary value problem (37) (38) (39) (40) Firstly, we prove the existence of solutions of Problem N for (1) by using the method of parameter extension. Theorem4Let the nonlinear complex equation(1) satisfy Condition C and (35), and the constantsq2,k1,k2,k4in (2),(3),(6) are small enough. Then Problem N for (1) is solvable. ProofLet us introduce a complex equation with the parametert∈ [0,1]: (41) (42) (43) (44) From (44) it follows (45) By Condition C and (35), it is easy to see that whereqj(j=1,2),kj(j=0,1,2) are non-negative constants satisfying the conditionq1+q2<1. Hence in which Moreover,wn+1-wnsatisfies the homogenous boundary conditions (46) (47) On the basis of Theorem 5.6, Chapter I, [7], we have the estimate S(wn+1-wn)≤M10|t-t0|(q1+q2+k0)S(wn-wn-1), (48) whereM10=M10(q0,p0,k0,β,D) (K=(K1,K2)) is a constant as stated in Theorem 5.6, Chapter I, [7]. Choosing that a positive numberδis sufficiently small so thatη=δM(q1+q2+k0)<1, it can be obtained that whent∈E, S(wn+1-wn)≤ηS(wn-wn-1)=ηnS(w1). Thus forn≥m>N, whereNis a positive integer. This showsS(wn-wm)→0 asn,m→∞.Hence there exists a functionw*(z) (R(z)w*(z)∈B), such thatS(w-w*)→0 asn→∞. It can be seen thatw*(z) is a solution of Problem N for (43) witht∈E. From Problem N for (43) witht=t0=0 is solvable, we may derived Problem N for (43) i.e. (41) witht=1 is solvable. In particular, Problem N for (41) withA(z)=(1-t)F(z,0,0,0,0),t=1, i.e.(1) is solvable. This completes the proof. Finally by using the result as in Theorem 4, we can derive the solvability results of Problem M for the complex equation(1) with some conditions as follows. Theorem5Suppose that the second order nonlinear complex equation (1) satisfy Condition C and (35). If the constantsq2,k1,k2,k4in (2),(3), (6) are all sufficiently small, then Problem M for (1) possesses the following results on solvability: (2)WhenK1<0,K2<0, Problem M is solvable under has 2N-[K1+1/2]-[K2+1/2] solvability conditions. Moreover, we can write down the solvability conditions of Problem M for all other cases. ProofWe first discuss the case:Kj≥0 (j=1, 2). Let the solution [w(z),U(z),V(z)] of Problem N for the complex equation (1) be substituted into (8)-(11). The functionshj(z)(j=1,2) in (9) are then determined. If the functions and the constants are equal to zero,namely the following equalities hold: hjl=0,l=1,…,N, whenKj≥0,j=1, 2, Similarly, other cases can be obtained. : [1]Vekua I N. Generalized Analytic Functions[M]. Oxford: Pergamon, 1962. [2]Lavrent'ev M A, Shabat B V. Methods of Function Theory of a Complex Variable[M]. Moscow: GITTL, 1958. [3]Bitsadze A V. Some Classes of Partial Differential Equations[M]. New York: Gordon and Breach, 1988. [4]Wen G C. Linear and Nonlinear Elliptic Complex Equations[M]. Shanghai: Shanghai Scientific and Technical Publishers, 1986. [5]Wen G C. Conformal Mappings and Boundary Value Problems[M]. Providence: Amer Math Soc, 1992. [6]Wen G C, Tai C W, Tian M Y. Function Theoretic Methods of Free Boundary Problems and Their Applications to Mechanics[M]. Beijing: Higher Education Press, 1996. [7]Wen G C. Approximate Methods and Numerical Alanalysis for Elliptic Complex Equations[M]. Amsterdam: Gordon and Breach, 1999. [8]Wen G C. Linear and Quasilinear Complex Equationsof Hyperbolic and Mixed Type[M]. London: Taylor & Francis, 2002. [9]Huang S, Qiao Y Y, Wen G C. Real and Complex Clifford Analysis[M]. Heidelberg: Springer Verlag, 2005. [10]Wen G C, Chen D C, Xu Z L. Nonlinear Complex Analysis and Its Applications[M]. Beijing: Science Press, 2008. [11]Wen G C. Recent Progress in Theory and Applications of Modern Complex Analysis[M]. Beijing: Science Press, 2010.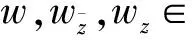
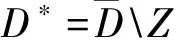
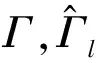
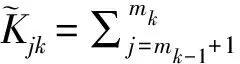

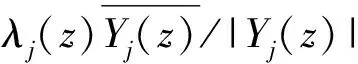
2 Estimates of Solutions of Discontinuous Mixed Problem for Elliptic ComplexEquations of Second Order
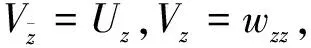
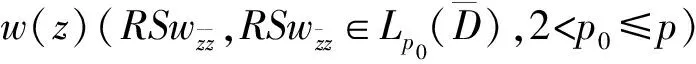
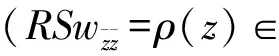
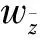
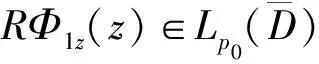
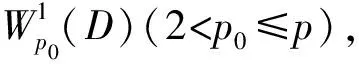
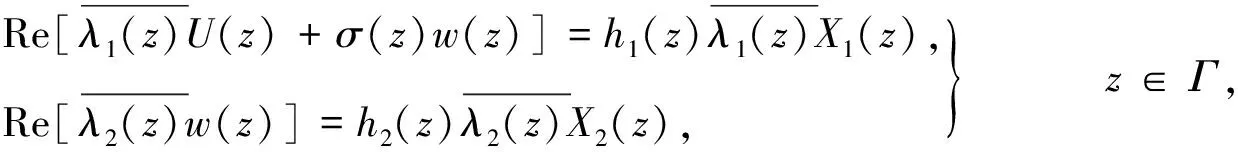
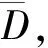
3 The Solvability of Discontinuous Mixed Problem for Elliptic Complex Equa-tions of Second Order