Weiping LI Xiugui LIU He WANG

1 Introduction

LetMbe a smooth compact closed manifold of dimensionn,and Ω?(M)be the space of smooth differential forms over R onM.We have the de Rham cochain complex(Ω?(M),d),whered:Ωp(M)→Ωp+1(M)is the exterior differentiation,and its cohomologyH?(M)(the de Rham cohomology).The de Rham cohomology with coefficients in a flat vector bundle is an extension of the de Rham cohomology.

The twisted de Rham cohomology was first studied by Rohm and Witten[13]for the antisymmetric field in superstring theory.By analyzing the massless fermion states in the string sector,Rohm and Witten obtained the twisted de Rham cochain complex(Ω?(M),d+H3)for a closed 3-formH3,and mentioned the possible generalization to a sum of odd closed forms.A key feature in the twisted de Rham cohomology is that the theory is not integer-graded but(likeK-theory)is filtered with the grading mod 2.This has a close relation with the twistedK-theory and the Atiyah-Hirzebruch spectral sequence(see[1]).

LetHbewhereis a closed(2i+1)-form.Then one can define a new operatorD=d+Hon Ω?(M),whereHis understood as an operator acting by exterior multiplication(for any differential formw,H(w)=H∧w).As in[1,13],there is a filtration on(Ω?(M),D)as follows:

This filtration gives rise to a spectral sequence

converging to the twisted de Rham cohomologyH?(M,H)with

For convenience,we first fix some notations in this paper.The notation[r]denotes the greatest integer part ofr∈R.In the spectral sequence(1.2),for any∈,[yp]k+lrepresents its class to whichsurvives inIn particular,as in Proposition 3.2,for=represents the de Rham cohomology classrepresents a class inwhich survives to

In[13,Appendix I],Rohm and Witten first gave a description of the differentialsd3andd5for the caseD=d+H3.Atiyah and Segal[1]showed a method about how to construct the differentials in terms of Massey products,and gave a generalization of Rohm and Witten’s result:The iterated Massey products withH3give(up to sign)all the higher differentials of the spectral sequence for the twisted cohomology(see[1,Proposition 6.1]).Mathai and Wu[9,p.5]considered the general case ofH=and claimed,without proof,thatd2=d4=···=0,whiled3,d5,···are given by the cup products withH3,H5,···and the higher Massey products with them.Motivated by the method in[1],we give an explicit description of the differentials in the spectral sequence(1.2)in terms of Massey products.

We now describe our main results.LetAdenote a defining system for then-fold Massey productandc(A)denote its related cocycle(see Definition 5.1).Then

by Definition 5.2.To obtain our desired theorems by specific elements of Massey products,we restrict the allowable choices of defining systems for Massey products(see[14]).By Theorems 4.1–4.2 in this paper,there are defining systems for the two Massey products that we need(see Lemma 5.1).The notationin Theorem 1.1 below denotes a cohomology class inH?(M)represented byc(A),whereAis a defining system obtained by Theorem 4.1(see Definition 5.3).Similarly,the notationin Theorem 1.2 below denotes a cohomology class inH?(M)represented byc(A),whereAis a defining system obtained by Theorem 4.2(see Definition 5.3).

Theorem 1.1For H=and(t≥1),the differential of the spectral sequence(1.2),i.e.,is given by

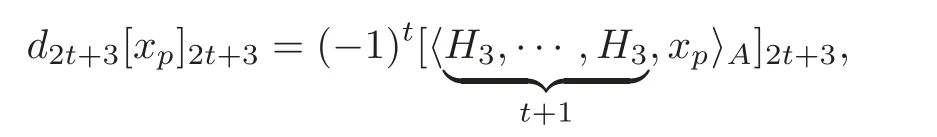
andis independent of the choice of the defining system A obtained from Theorem4.1.

Specializing Theorem 1.1 to the caseH=we obtain

Obviously,much information has been concealed in the above expression.In particular,we give a more explicit expression of differentials for this special case,which is compatible with Theorem 1.1(see Remark 5.6).

Theorem 1.2For H=(s≥1)only and(t≥1),the differential of the spectral sequence(1.2),i.e.,:is given by

andis independent of the choice of the defining system B obtained from Theorem4.2.

Atiyah and Segal[1]gave the differential expression in terms of Massey products whenH=H3(see[1,Proposition 6.1]).Obviously,the result of Atiyah and Segal is a special case of Theorem 1.2.

Some of the results above are known to experts in this field,but there is a lack of mathematical proof in the literature.

This paper is organized as follows.In Section 2,we recall some backgrounds about the twisted de Rham cohomology.In Section 3,we consider the structure of the spectral sequence converging to the twisted de Rham cohomology,and give the differentialsdi(1≤i≤3)and(k≥1).With the formulas of the differentials inin Section 4,Theorems 1.1 and 1.2 are proved in Section 5.In Section 6,we discuss the indeterminacy of differentials of the spectral sequence(1.2).

2 Twisted de Rham Cohomology

For completeness,in this section,we recall some knowledge about the twisted de Rham cohomology.LetMbe a smooth compact closed manifold of dimensionn,and Ω?(M)be thespace of smooth differential forms onM.We have the de Rham cochain complex(Ω?(M),d)with the exterior differentiationd:and its cohomologyH?(M)(the de Rham cohomology).

LetHdenotewhereis a closed(2i+1)-form.Define a new operatorD=d+Hon Ω?(M),whereHis understood as an operator acting by exterior multiplication(for any differential formw,H(w)=H∧w,also denoted byH∧).It is easy to show that

However,Dis not homogeneous on the space of smooth differential forms Ω?(M)=

Define Ω?(M)to be a new(mod 2)grading as follows:

where

ThenDis homogenous for this new(mod 2)grading,

Define the twisted de Rham cohomology groups ofMas follows:

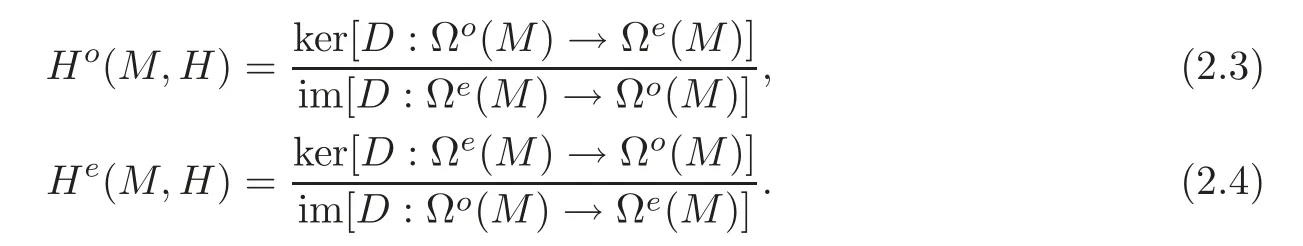
Remark 2.1(i)The twisted de Rham cohomology groupsH?(M,H)(?=o,e)depend on the closed formHbut not just on its cohomology class.IfHandH′are cohomologous,thenH?(M,H)H?(M,H′)(see[1,Section 6]).

(ii)The twisted de Rham cohomology is also an important homotopy invariant(see[9,Section 1.4]).

LetEbe a flat vector bundle overM,and Ωi(M,E)be the space of smooth differentiali-forms onMwith values inE.A flat connection onEgives a linear map

such that for any smooth functionfonMand anyω∈Ωi(M,E),

Similarly,define Ω?(M,E)to be a new(mod 2)grading as follows:

where

Thenis homogenous for the new(mod 2)grading,

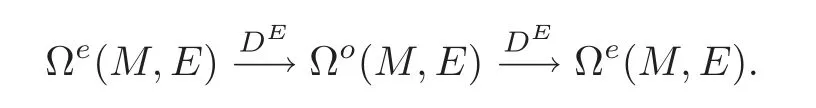
Define the twisted de Rham cohomology groups ofEas follows:

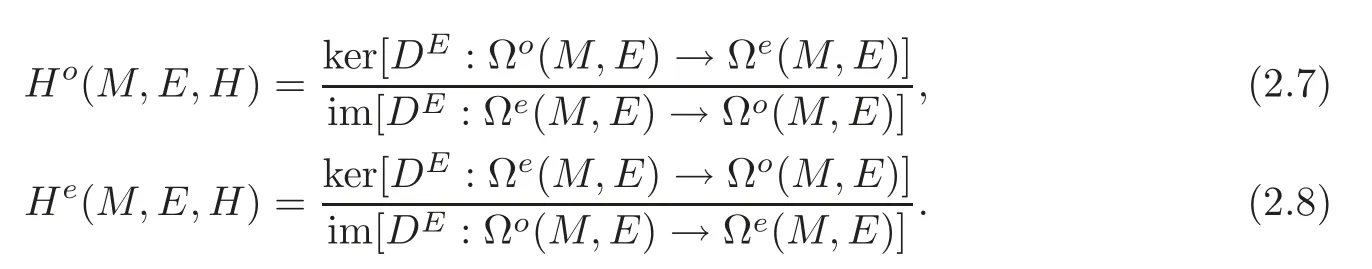
Results proved in this paper are also true for the twisted de Rham cohomology groupsH?(M,E,H)(?=o,e)with twisted coefficients inEwithout any change.

3 A Spectral Sequence for Twisted de Rham Cohomology and Its Differentials di(1i3),(k1)

RecallD=d+HandH=whereis a closed(2i+1)-form.Define the usual filtration on the graded vector space Ω?(M)to be

andK=K0= Ω?(M).The filtration is bounded and complete,

We haveD(Kp)?The differentialD(=d+H)does not preserve the grading of the de Rham complex.However,it does preserve the filtration

The filtrationgives an exact couple(with bidegree)(see[12]).For eachp,Kpis a graded vector space with

whereandThe cochain complex(Kp,D)is induced byD:Ω?(M)?→Ω?(M).In a way similar to(2.4),there are two well-defined cohomology groupsNote that a cochain complex with grading

derives cohomology groupsandSinceD(we haveD=0 in the cochain complex

Lemma 3.1For the cochain complexwe have

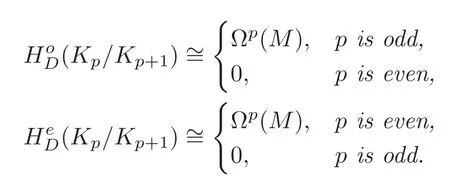
ProofIfpis odd,then

We have

Similarly,for evenp,we have

By the filtration(3.1),we obtain a short exact sequence of cochain complexes

which gives rise to a long exact sequence of cohomology groups

Note that in the exact sequence above,

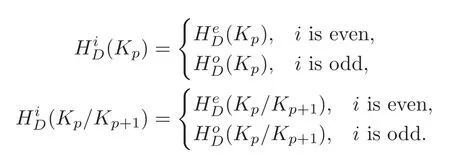
Let

We get an exact couple from the long exact sequence(3.3)

withi1of bidegree(?1,1),j1of bidegree(0,0)andk1of bidegree(1,0).

We haved1=with bidegree(1,0),and=0.By(3.5),we have the derived couple

by the following:

(1)=i1D?,?1,E?,?2=Hd1(E?,?1).

(2)i2=i1also denoted byi1.

(3)Ifa2=define()=where[]d1denotes the cohomology class inHd1

(4)For[b]d1∈=define

The derived couple(3.6)is also an exact couple,andj2andk2are well defined(see[6,12]).

Proposition 3.1(i)There exists a spectral sequencederived from the filtrationwhere=andThe bidegree of dris(r,1?r).

(ii)The spectral sequenceconverges to the twisted de Rham cohomology

ProofSince the filtration is bounded and complete,the proof follows from the standard algebraic topology method(see[12]).

Remark 3.1(1)Note that

Then we have thatare 2-periodic oni.Consequently,the spectral sequenceis 2-periodic onq.

(2)There is also a spectral sequence converging to the twisted cohomologyH?(M,E,H)for a flat vector bundleEoverM.

Proposition 3.2For the spectral sequence in Proposition3.1,

(i)The-term is given by

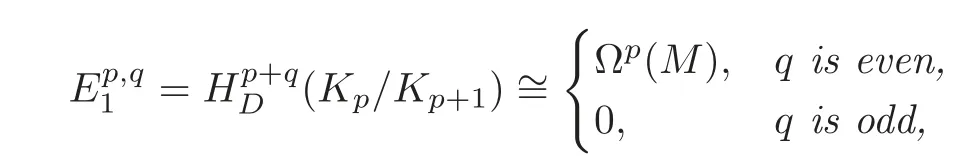
and d1xp=dxpfor any xp∈

(ii)The -term is given by

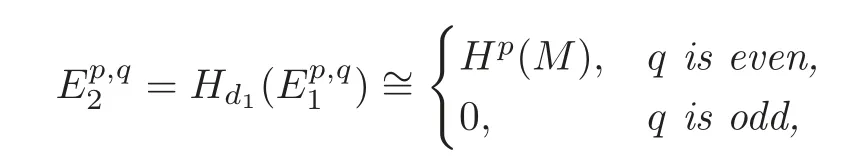
and d2=0.

(iii)=and d3[xp]=

Proof(i)By Lemma 3.1,we have the-term as desired,and by definition,we obtain:We only need to consider the case whenqis even,otherwised1=0.By(3.2)for oddp(the case,whenpis even,is similar),we have a large commutative diagram

where the rows are exact and the columns are cochain complexes.

Letxp∈Ωp(M)and

be an(inhomogeneous)form,whereis a(p+2i)-form(0≤i≤Thenx∈jx=xpandDx∈AlsoDx∈By the definition of the homomorphismδin(3.3),we have

where[]Dis the cohomology class inThe class[Dx]Dis well defined and independent of the choices of(1≤i≤(see[3,p.116]).

Choose=0(1≤i≤[Then we have

Thus,one obtains

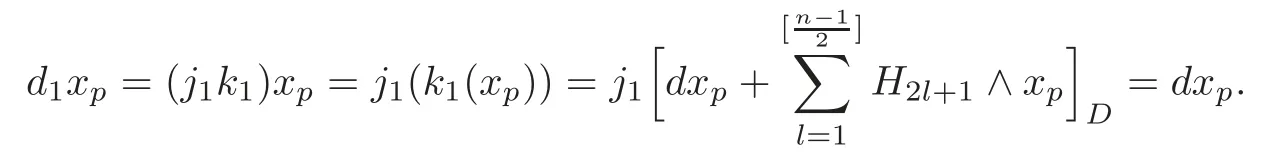
(ii)By the definition of the spectral sequence and(i),one obtains that(M)whenqis even,and=0 whenqis odd.Noted2:It follows thatd2=0 by degree reasons.

(iii)Note thatimpliesdxp=0.Choosing=0 for 1≤i≤we get

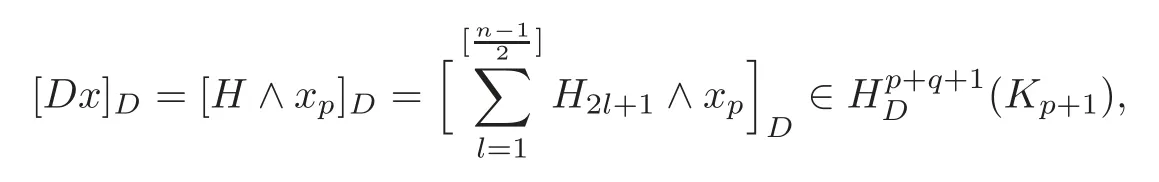
wherexis given in the proof of(i).Note

It follows that

where the first,second and fourth identities follow from the definitions ofd3,k3andj3,respectively,and the third and last identities follow from(3.10)and(3.11),respectively.By(ii),d2=0,soThen we have

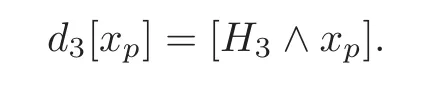
Corollary 3.1d2k=0for k≥1.Therefore,for k≥1,

ProofNoteBy Proposition 3.2(ii),ifqis odd,then=0,which implies that=0.By degree reasons,we have=0 andfork≥1.

The differentiald3for the caseH=H3is shown in[1,Section 6],and the-term is also known.

4 Differentials( 1)in Terms of Cup Products

In this section,we will show that the differentials(t≥1)can be given in terms of cup products.

We first consider the general case ofH=we letx=∈(M)).Then we have

Denotey=Dx=where

Theorem 4.1For(t≥1),there exist(1≤i≤t),such that=0(0≤j≤t)and

where the(p+2i)-formdepends on t.

ProofThe theorem is shown by mathematical induction ont.

Whent=1,implies thatdxp=0 and=0 by Proposition 3.2.Thus there exists a(p+2)-formv1,such thatWe can choose=v1to get+=0 from(4.2).Noting

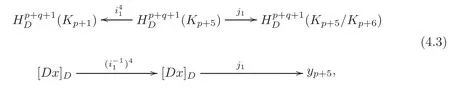
we obtain

The reasons for the identities in(4.4)are similar to those of(3.12).Thus,we have

where the first identity follows from(4.4)and the definition ofin(4.2),and the second one follows from the fact thatvanishes inHence the result holds fort=1.

Suppose that the result holds fort≤m?1.Now we show that the theorem also holds fort=m.

Fromwe haveand=0.By induction,there exist(1≤i≤m?1),such that

Byd2m=0 and the last equation in(4.5),there exists a(p+2)-formsuch that

By induction andthere exist(1≤i≤m?2),such that

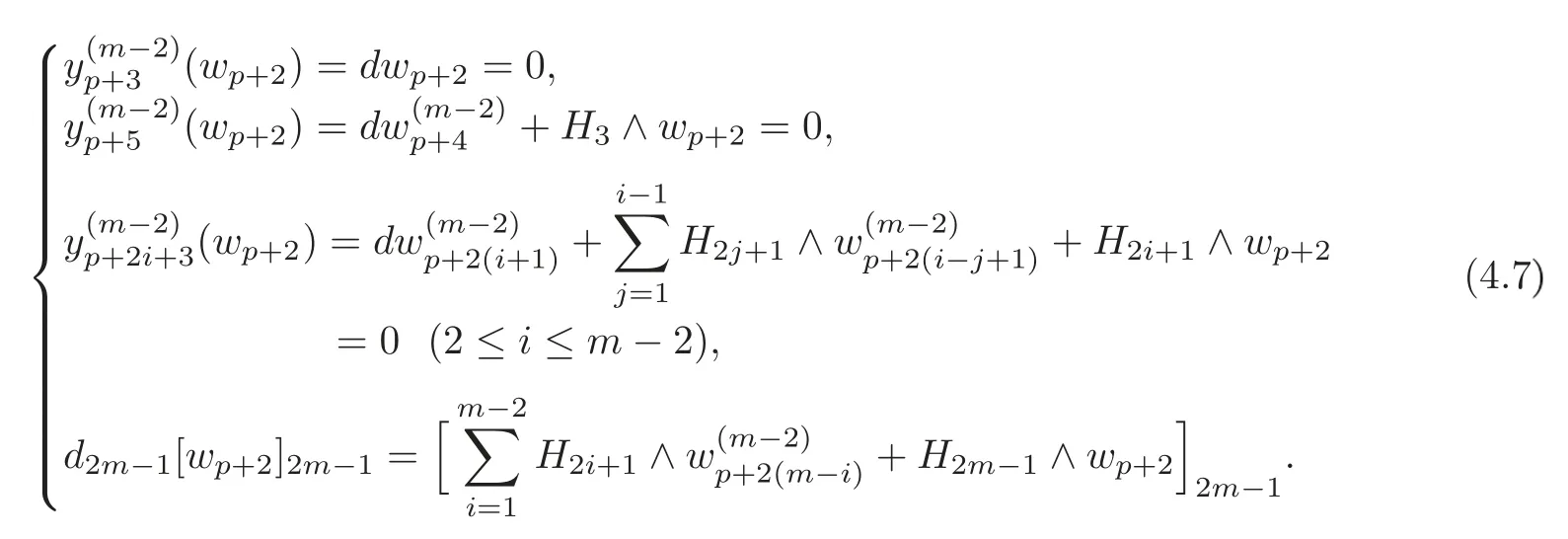
By(4.6)and the last equation in(4.7),we obtain

Note that=0,and it follows that there exists a(p+4)-formsuch that

Keeping the same iteration process as mentioned above,we have

Byd6=0,it follows that there exists a(p+2(m?2))-formsuch that

By induction andthere existssuch that

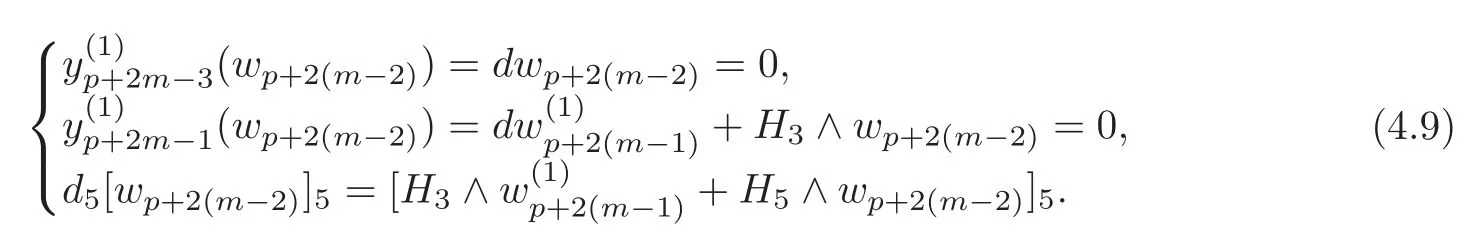
By(4.8),the last equation in(4.9)andd4=0,it follows that there exists a(p+2(m?1))-formsuch that

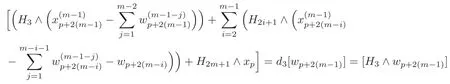
and==0.Thus there exists a(p+2m)-formsuch that

Comparing(4.10)with(4.2),we choose at this time

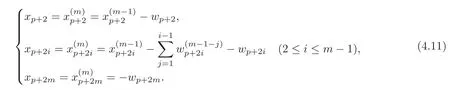
From(4.2),by a direct computation,we have

Note

By the similar reasons as in(3.12),the following identities hold:

So we have

showing that the result also holds fort=m.

The proof of the theorem is completed.

Remark 4.1Note that(1≤i≤t)depend ont,and thatdepend on the conditiongenerally(1≤i≤t)are related to(1≤j≤t?1,j≤i).

Now we consider the special case in whichH=(s≥1)only.For this special case,we will give a more explicit result which is stronger than Theorem 4.1.

Forx=we have

Denote

ThenDx=

Theorem 4.2For H=(s≥1)only and(t≥1),there exist==0and=0for1≤i≤1≤j≤s?1and1≤k≤t?s,such that=0(0≤u≤t)and

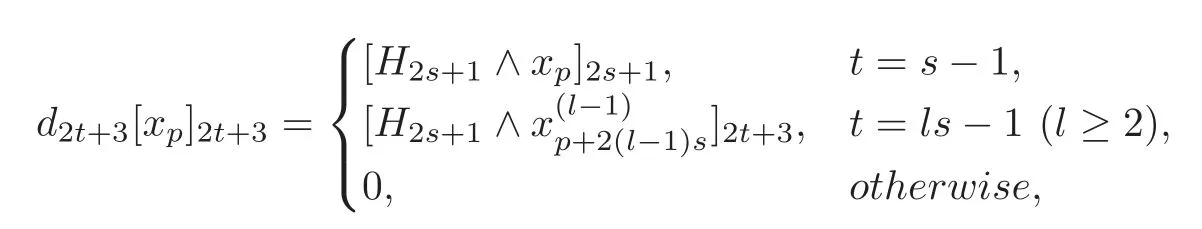
where the(p+2is)-formdepend on

ProofWe prove the theorem by mathematical induction ons.

Whens=1,the result follows from Theorem 4.1.

Whens≥2,we prove the result by mathematical induction ont.We first show that the result holds fort=1.Note thatimplies=0.Choose=0 and make=0.

(i)Whens=2,by(4.4),we have

(ii)Whens≥3,by(4.4),we have

Combining(i)and(ii),we have that the theorem holds fort=1.

Suppose that the theorem holds fort≤m?1.Now we show that the theorem also holds fort=m.

Case 12≤m≤s?1.

By induction,the theorem holds for 1≤t≤m?1.Choosing=0(1≤i≤m),from(4.15),we easily get that=0(0≤j≤m).By(4.14)–(4.15),we have

Case 2m=ls?1(l≥2).

By induction,the theorem holds fort=m?1=ls?2.Thus,there exist==0 and=0 for 1≤i≤l?1,1≤j≤s?1 and 1≤k≤s?2,such that=0(0≤u≤ls?2).Choosing=0,by(4.15),we get

Then we have

Case 3m=ls(l≥1).

By induction,there exist=0 andxp+2(l?1)s+2k=0 for 1≤i≤l?1,1≤j≤s?1 and 1≤k≤s?1,such that=0(0≤u≤ls?1).By the same method as in Theorem 4.1,one has that there exist==0 and=0 for 1≤i≤l,1≤j≤s?1 and 1≤k≤s?1,such that=0(0≤u≤ls).By(4.14)–(4.15)and=0,we have

Case 4ls＜m＜(l+1)s?1(l≥1).

By induction,there exist===0 and=0 for 1≤i≤l,1≤j≤s?1 and 1≤k≤m?ls?1,such that=0(0≤u≤m?1).Choose=0 and make=0.By(4.14)–(4.15)and=0,we have

Combining Cases 1–4,we have that the result holds fort=m,and the proof is completed.

Remark 4.2(1)Theorems 4.1–4.2 show that the differentials in the spectral sequence(1.2)can be computed in terms of cup products withThe existence of’s in Theorems 4.1–4.2 plays an essential role in proving Theorems 1.1–1.2,respectively.Theorems 4.1–4.2 give a description of the differentials at the level offor the spectral sequence(1.2),which was ignored in the previous studies of the twisted de Rham cohomology in[1,9].

(2)Note that Theorem 4.2 is not a corollary of Theorem 4.1,and it can not be obtained from Theorem 4.1 directly.

5 Differentials (t ≥ 1)in Terms of Massey Products

The Massey product is a cohomology operation of higher order introduced in[8],which generalizes the cup product.May[10]showed that the differentials in the Eilenberg-Moore spectral sequence associated with the path-loop fibration of a path connected,simply connected space are completely determined by higher order Massey products.Kraines and Schochet[5]also described the differentials in Eilenberg-Moore spectral sequence by Massey products.Inorder to describe the differentials(t≥1)in terms of Massey products,we first recall brief l y the definition of Massey products(see[4,10–12]).Then the main theorems in this paper will be shown.

Because of different conventions in the literature used to define Massey products,we present the following definitions.Ifx∈Ωp(M),the symbolwill denoteWe first define the Massey triple product.

Letbe closed differential forms onMof degreeswith=0 and=0,where[]denotes the de Rham cohomology class.Thus,there are differential formsv1of degreer1+r2?1 andv2of degreer2+r3?1,such thatandDefine the?1)-form

Thenωsatisfies

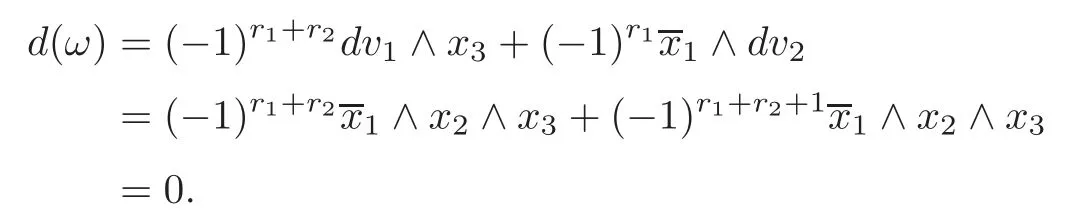
Hence a set of all the cohomology classes[ω]obtained by the above procedure is defined to be the Massey triple productofx1,x2andx3.Due to the ambiguity ofvi,i=1,2,the Massey triple productis a representative of the quotient group

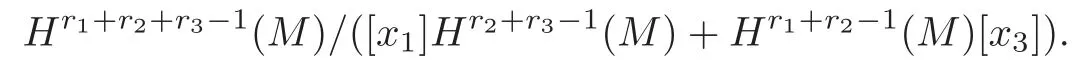
Definition 5.1Let(Ω?(M),d)be de Rham complex,and···,xnbe closed differential forms on M with(M).A collection of forms,A=for1≤i≤j≤k andis said to be a defining system for the n-fold Massey product〉if

The(r1+···+rn?n+2)-dimensional cocycle,c(A),defined by

is called the related cocycle of the defining system A.

Remark 5.1There is a unique matrix associated to each defining systemAas follows:

Definition 5.2The n-fold Massey product〉is said to be defined,if there is a defining system for it.If it is defined,thenconsists of all classes w∈for which there exists a defining system A,such that c(A)represents w.

Remark 5.2There is an inherent ambiguity in the definition of the Massey product arising from the choices of defining systems.In general,then-fold Massey product may or may not be a coset of a subgroup,but its indeterminacy is a subset of a matrix Massey product(see[10,Section 2]).

Based on Theorems 4.1–4.2,we have the following lemma on defining systems for the two Massey products we consider in this paper.

Lemma 5.1(1)For(t≥1),there are defining systems forxp〉obtained from Theorem4.1.

(2)Forwhen t=ls?1(l≥2),there are defining systems forobtained from Theorem4.2.

Proof(1)From Theorem 4.1,there exist(1≤j≤t),such that=0(0≤i≤t)and=+By Theorem 4.1 and(4.2),there exists a defining systemA=(ai,j)for〉as follows:

to which the matrix associated is given by

The desired result follows.

(2)By Theorem 4.2,there exist=0 and=0 for 1≤i≤l?1,1≤j≤s?1 and 1≤k≤s?1,such that=0(0≤i≤t)andBy Theorem 4.2 and(4.15),there also exists a definingsystemA=foras follows:

to which the matrix associated is given by

The desired result follows.

To obtain our desired theorems by specific elements of Massey products,we restrict the allowable choices of defining systems for the two Massey products in Lemma 5.1(see[14]).By Lemma 5.1,we give the following definitions.

Definition 5.3(1)Given a class(t≥1),a specific element of(t+2)-fold Massey productdenoted byis a class in(M)represented by c(A),where A is a defining system obtained from Theorem4.1.We define the(t+2)-fold allowable Massey productto be the set of all the cohomology classes w∈(M)for which there exists a defining system A obtained from Theorem4.1,such that c(A)represents w.

(2)Similarly,given a class(t≥1),when t=ls?1(l≥2),we definethe specific element of(l+1)-fold Massey product〉and the(l+1)-foldallowable Massey productby replacing Theorem4.1by Theorem4.2in(1).

Remark 5.3(1)From Definition 5.3,we can get the following:

(2)The allowable Massey productis less ambiguous than the general Massey productTakein Definition 5.3 for example.SupposeH=By Theorem 4.1 and(4.2),there existsuch that=0(0≤i≤1)and=By Lemma 5.1,we get a defining systemAforand its related cocyclec(A)=?Thus,we have

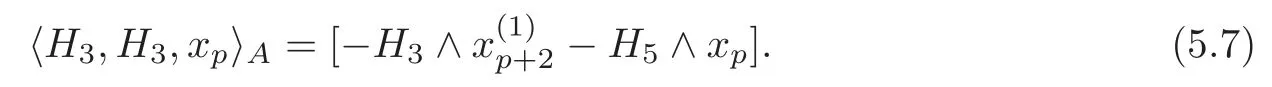
Obviously,the indeterminacy of the allowable Massey product(M).However,in the general case,the indeterminacy of the Massey product〉is(M)+

Similarly,the allowable Massey productis less ambiguous than the general Massey product

Now we begin to prove our main theorems.

Proof of Theorem 1.1By Lemma 5.1(1),there exist defining systems forgiven by Theorem 4.1.For any defining systemA=(ai,j)given by Theorem 4.1,by(5.4),we have

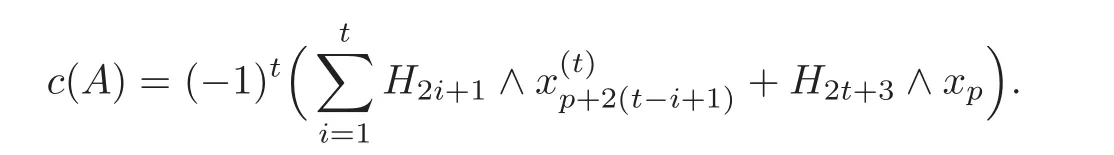
By Definition 5.3,we have

Then by Theorem 4.1,we have

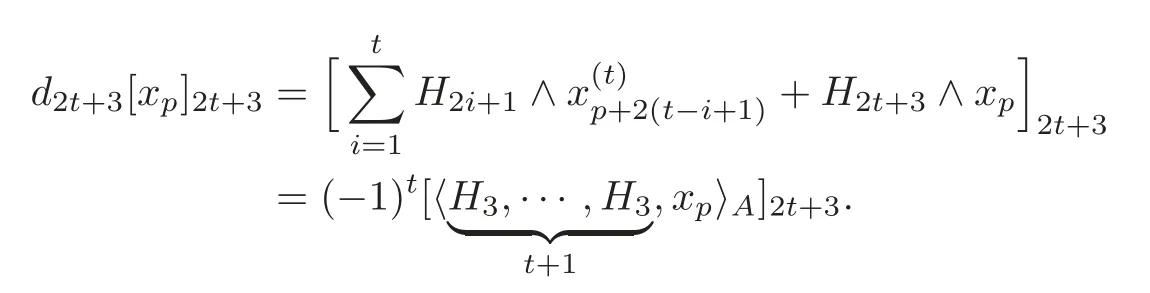
Thus,we have

By the arbitrariness ofA,we have thatis independent of the choice of the defining systemAobtained by Theorem 4.1.

Example 5.1For formal manifolds,which are manifolds with vanishing Massey products,it is easy to get

by Theorem 1.1.Note that simply connected compact Khler manifolds are an important class of formal manifolds(see[2]).

Remark 5.4(1)From the proof of Theorem 1.1,we have that the specific element

represents a class inFor two different defining systemsA1andA2given by Theorem 4.1,we have

generally.However,in the spectral sequence(1.2),we have

(2)Since the indeterminacy ofdoes not affect our results,we will not analyze the indeterminacy of Massey products in this paper.

(3)By Theorem 1.1,fort≥1,which is expressed only byH3andxp.From the proof of Theorem 1.1,we know that the above expression conceals some information,because the otheraffect the result implicitly.

We have the following corollary(see[1,Proposition 6.1]).

Corollary 5.1For H=H3only and(t≥1),we have that in the spectral sequence(1.2),

and[is independent of the choice of the defining system A obtained from Theorem4.1.

Remark 5.5(1)Because the definition of Massey products is different from the definition in[1],the expression of differentials in Corollary 5.1 differs from the one in[1,Proposition 6.1].

(2)The two specific elements of〉in Theorem 1.1 and Corollary 5.1 are completely different,and equal[c(A1)]and[c(A2)],respectively,wherec(Ai)(i=1,2)are related cocycles of the defining systemsAi(i=1,2)obtained from Theorem 4.1.The matrices associated to the two defining systems are given by

and

respectively.Here(1≤i≤t)in the first matrix are different from those in the second one.

ForH=(s≥2)only(i.e.,in the caseHi=0,i2s+1)and(t≥1),we make use of Theorem 1.1 to get

Obviously,some information has been concealed in the expression above.Another description of the differentials for this special case is shown in Theorem 1.2.

Proof of Theorem 1.2Whent=s?1,the result follows from Theorem 4.2.

Whent=ls?1(l≥2),from Lemma 5.1(2),we know that there exist defining systems forobtained from Theorem 4.2.For any defining systemBgiven by Theorem 4.2,by(5.6),we getc(B)=(?1By Definition 5.3,

Then by Theorem 4.2,we have

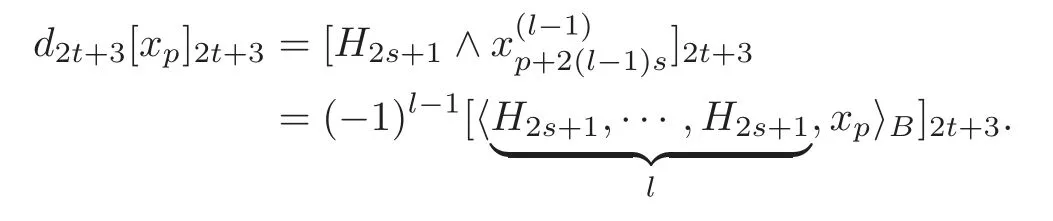
Thus

By the arbitrariness ofB,we have thatis independent of the choice of the defining systemBobtained from Theorem 4.2.

For the rest cases oft,the results follow from Theorem 4.2.

The proof of this theorem is completed.

Remark 5.6We now use the special caseH=H5andto illustrate the compatibility between Theorems 1.1 and 1.2 fors=2 andt=3.

Note that in this case,we haveH3=0 andHi=0 fori＞5.By Theorem 1.1,we get the corresponding matrix associated to the defining systemAfor

and

By Theorem 1.2,in this case,the matrix associated to the defining systemBfor

and

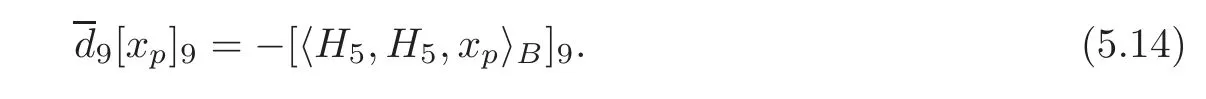
We claim that=For any defining systemBabove,there is a defining system

forwhich can be obtained from Theorem 4.1,such that

HenceOn the other hand,for any defining systemAabove,there also exists a defining system

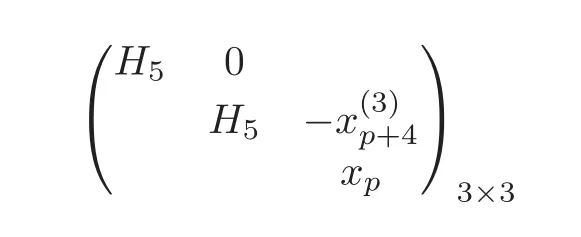
forwhich can be obtained from Theorem 4.2,such that

Thereforeand thus the claim follows.

By Theorem 1.1 and Remark 5.3,we have

By Theorem 1.2,By Proposition 3.4,=0.It follows that

By Theorems 1.1 and 4.1,we have

whereis an arbitrary(p+2)-form satisfying=0∧zp.By Remark 5.4(2),we take=0.Then we have=0,i.e.,0.At the same time,we also have=0 from Theorem 1.2.Thus=0.

Byfor 1≤i≤7 and=we can conclude that=from(5.12)and(5.14).

6 The Indeterminacy of Differentials in the Spectral Sequence(1.2)

LetThe indeterminacy of[xp]is a normal subgroupGofH?(M),which means that if there is another element[yp]∈Hp(M),which also represents the classthen

In this section,we will show that forH=the indeterminacy of the differential∈is a normal subgroup ofH?(M).

From the long exact sequence(3.3),we have a commutative diagram

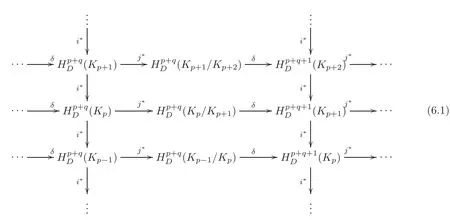
in which any sequence consisting of a vertical mapfollowed by two horizontal mapsandδand then a vertical mapi?followed again by,δ,and iteration of this is exact.From this diagram,there is a spectral sequence,in whichand forr≥2,isdefined to be the quotientwhere

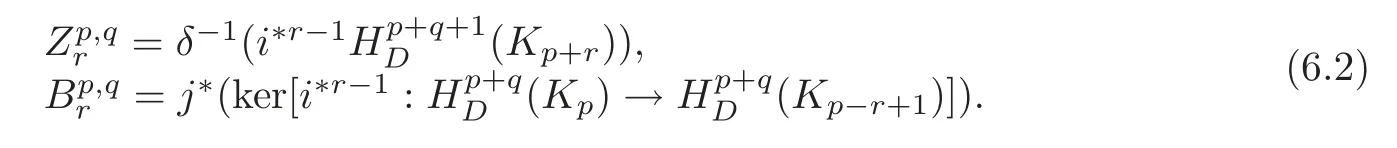
We also have a sequence of inclusions

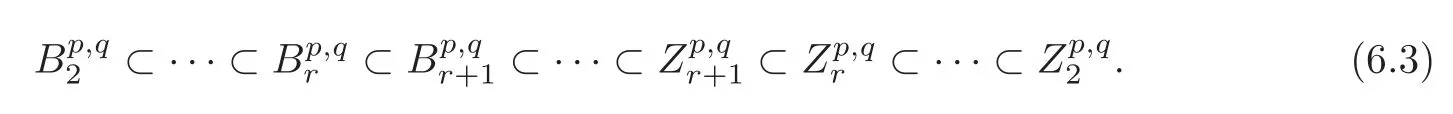
By[6–7],thedefined above is the same as the one in the spectral sequence(1.2).A similar argument about a homology spectral sequence is given in[15,p.472–473].

Theorem 6.1Let H=(r≥3).Then the indeterminacy ofis the following normal subgroup of Hp(M):

where d is just the exterior differentiation,and δ is the connecting homomorphism of the long exact sequence induced by the short exact sequence of cochain complexes

ProofFrom the above tower(6.3),we get a tower of subgroups of

Note

It follows that the indeterminacy of[xp]is the normal subgroupofHp(M).

From the short exact sequences of cochain complexes

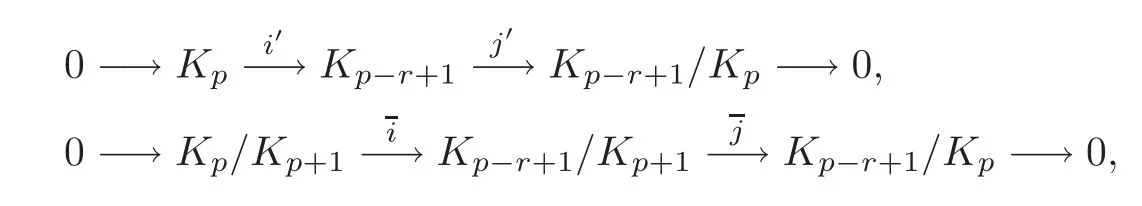
we can get the following long exact sequence of cohomology groups:

whereandare the connecting homomorphisms.

Combining(3.3)and(6.4),we have the following commutative diagram of long exact sequences:

Using the above commutative diagram and the fact thatwe have

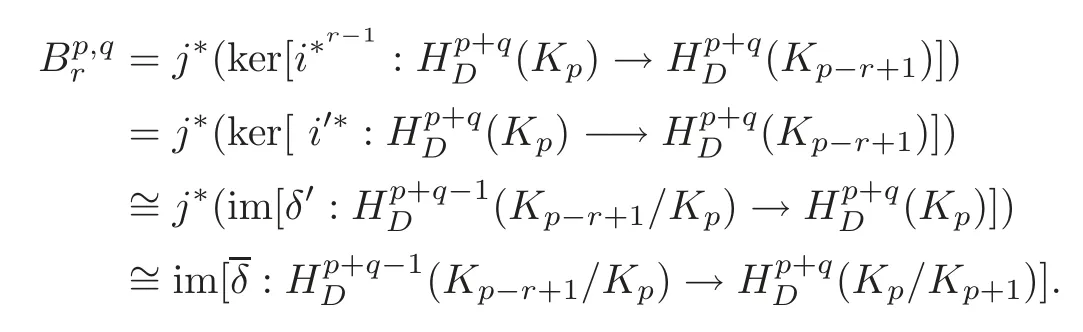
Whenr=2,from(6.5),we have

From(3.4),it follows that=d1.By Proposition 3.2,=d.Thus,we have

The desired result follows.

By Theorem 6.1,we obtain the following corollary.

Corollary 6.1In Theorem1.1,forwe have that the indeterminacy ofis a normal subgroup of(M)

where d is just the exterior differentiation,and δ is the connecting homomorphism of the long exact sequence induced by the short exact sequence of cochain complexes

ProofIn Theorem 6.1,r,pandqare replaced by 2t+3,p+2t+3 andq?2t?2,respectively.Then the desired result follows.

AcknowledgementsThe authors would like to express gratitude to Professor Jim Stashefffor his helpful comments,and thank the referees for their suggestions.

[1]Atiyah,M.and Segal,G.B.,TwistedK-Theory and Cohomology,Inspired by S.S.Chern,Nankai Tracts Math.,11,World Sci.Publ.,Hackensack,NJ,2006,5–43.

[2]Deligne,P.,Griffiths,P.,Morgan,J.and Sullivan,D.,Real homotopy theory of Khler manifolds,Invent.Math.,29(3),1975,245–274.

[3]Hatcher,A.,Algebraic Topology,Cambridge University Press,Cambridge,2002.

[4]Kraines,D.,Massey higher products,Trans.Amer.Math.Soc.,124,1966,431–449.

[5]Kraines,D.and Schochet,C.,Differentials in the Eilenberg-Moore spectral sequence,J.Pure Appl.Algebra,2(2),1972,131–148.

[6]Massey,W.S.,Exact couples in algebraic topology,I,II,Ann.of Math.(2),56,1952,363–396.

[7]Massey,W.S.,Exact couples in algebraic topology,III,IV,V,Ann.of Math.(2),57,1953,248–286.

[8]Massey,W.S.,Some higher order cohomology operations,1958 Symposium Internacional de Topologa Algebraica International Symposium on Algebraic Topology,Universidad Nacional Autnoma de M′exico and Unesco,Mexico,1958,145–154.

[9]Mathai,V.and Wu,S.,Analytic torsion for twisted de Rham complexes,J.Diff.Geom.,88(2),2011,297–332.

[10]May,J.P.,Matric Massey products,J.Algebra,12,1969,533–568.

[11]May,J.P.,The cohomology of augmented algebras and generalized Massey products for DGA-algebras,Trans.Amer.Math.Soc.,122,1966,334–340.

[12]McCleary,J.,A User’s Guide to Spectral Sequences,2nd Edition,Cambridge University Press,Cambridge,2001.

[13]Rohm,R.and Witten,E.,The antisymmetric tensor field in superstring theory,Ann.Physics,170(2),1986,454–489.

[14]Sharif i,R.T.,Massey products and ideal class groups,J.Reine Angew.Math.,603,2007,1–33.

[15]Spanier,E.W.,Algebraic Topology,Springer-Verlag,New York,Berlin,1981.