ZHAO Lan-hao (趙蘭浩), MAO Jia (毛佳), LIU Xiao-qing (劉曉青), LI Tong-chun (李同春)

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China,

E-mail: zhaolanhao@hhu.edu.cn

Numerical simulation of landslide-generated impulse wave*

ZHAO Lan-hao (趙蘭浩), MAO Jia (毛佳), LIU Xiao-qing (劉曉青), LI Tong-chun (李同春)

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China,

E-mail: zhaolanhao@hhu.edu.cn

(Received February 21, 2014, Revised March 5, 2014)

A numerical model is proposed for the simulation of impulse waves generated by landslides. The fluid-like landslide is modeled as a generalized non-Newtonian visco-plastic fluid. The conservative level set method is extended to then-phase flow and applied to capture the interfaces of air, water and landslide. Numerical results show an excellent performance of the current model to capture the whole process of the landslide and the impulse wave generation.

landslide, impulse wave, three-phase flow, conservative level set

Landslides represent one of the most destructive hazards in nature. The enormous damage associated with these phenomena is not only due to the large amount of mud and debris materials involved but also due to the potentially large generated impulse waves. Many instances were reported all over the world, among which are two of the most devastating examples: the 1958 Lituya Bay case where a landslide tsunami destroyed a forest up to a run-up height of 524 m above the mean sea level, and the 1963 Vaiont case in Northern Italy, where an impulse wave overtopped a dam by more than 70 m and caused about 2000 casualties[1]. It is, therefore, of great importance to understand and estimate the behavior and characteristics of landslide-generated impulse waves. Despite a considerable number of general model studies, a numerical prediction of impulse wave features remains desirable.

There are a strong interaction between three pha-ses: gas (air), liquid (water) and solid (landslide material) in the landslide wave generation and propagation. When a three-phase model is employed to simulate these phenomena, how to capture the interfaces between different phases becomes a key issue. The conservative level set (CLS) method, originally proposed for the two-phase flow by Elin and Olsson[2,3], enjoys excellent mass conservation properties in interface capturing and was successfully employed in many applications[4,5].

In this work, the CLS method is extended to then-phase flow and is employed to capture the interfaces of different phases in the landslide and the impulse wave generation. The general Navier-Stocks equations and the proper constitutive model are then employed to describe the motion of the three types of fluid including the air, the water and the landslide.

In the CLS method, a domainΩis divided into two sub-domainsΩ1andΩ2occupied by two fluids with an interfaceΓ12, as shown in Fig.1(a). The Heaviside functionHis used to describe the interface

The material property (MP), is calculated as follows

where MPican be the density, the viscosity, the yield strength, etc. of fluidi.

Fig.1 Definitions ofn-phase flow problems using indicator functions

The basic idea of the CLS method can be extended to the three-phase orn-phase flow by defining more indicator functions. As shown in Fig.1(b)), two indicator functions,H1,H2, are employed to describe the interfaces between the three sub-domains1Ω, 2Ω, and3Ωfor the three-phase flow. In this case, the material property MP can be calculated as

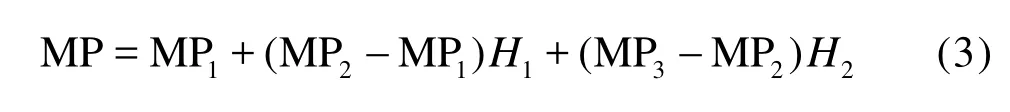
Generally speaking,n-1 indicator functionsHi(i=1…n-1) are defined to describe the interfaces for then-phase flow, for instance, the four-phase flow, as shown in Fig.1(c):

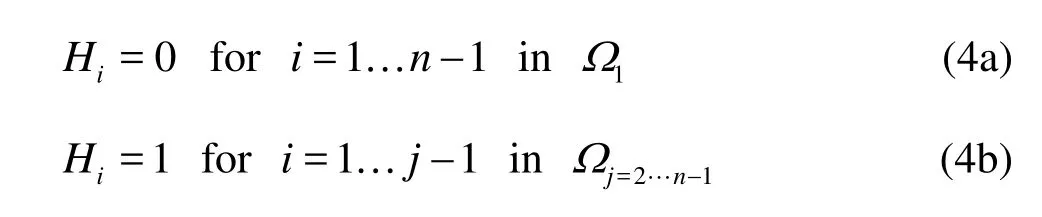
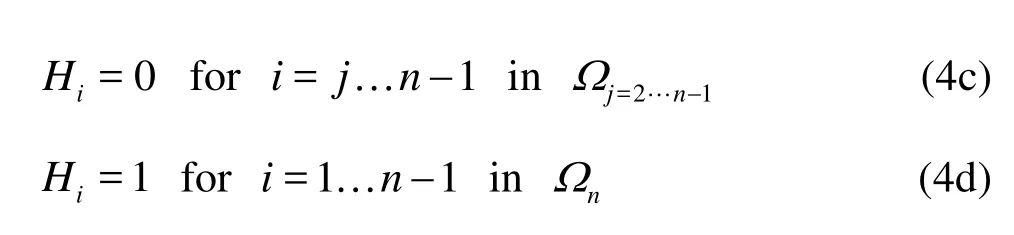
The material properties MP can be calculated in the same way as the two-phase case

The generalized visco-plastic fluid model proposed by Chen and Ling[6]is employed in this study as the constitutive model

whereτis the stress tensor,pis the pressure,τy0is the fluid yield stress,φis the internal friction angle,Dis the strain rate tensor,I2Dis the second invariant ofD,1μand2μare the viscosity coefficients and1ηand2ηare the flow behavior exponents, respectively.

Fig.2 Photomontage of the 1958 Lituya Bay case showing the boundaries of the slide area and the maximum wave run-up height of 524 m on the opposite shore of the bay[7]

Fig.3 Numerical simulation results of the different phases due to the landslide impact. Time increment is 5 s

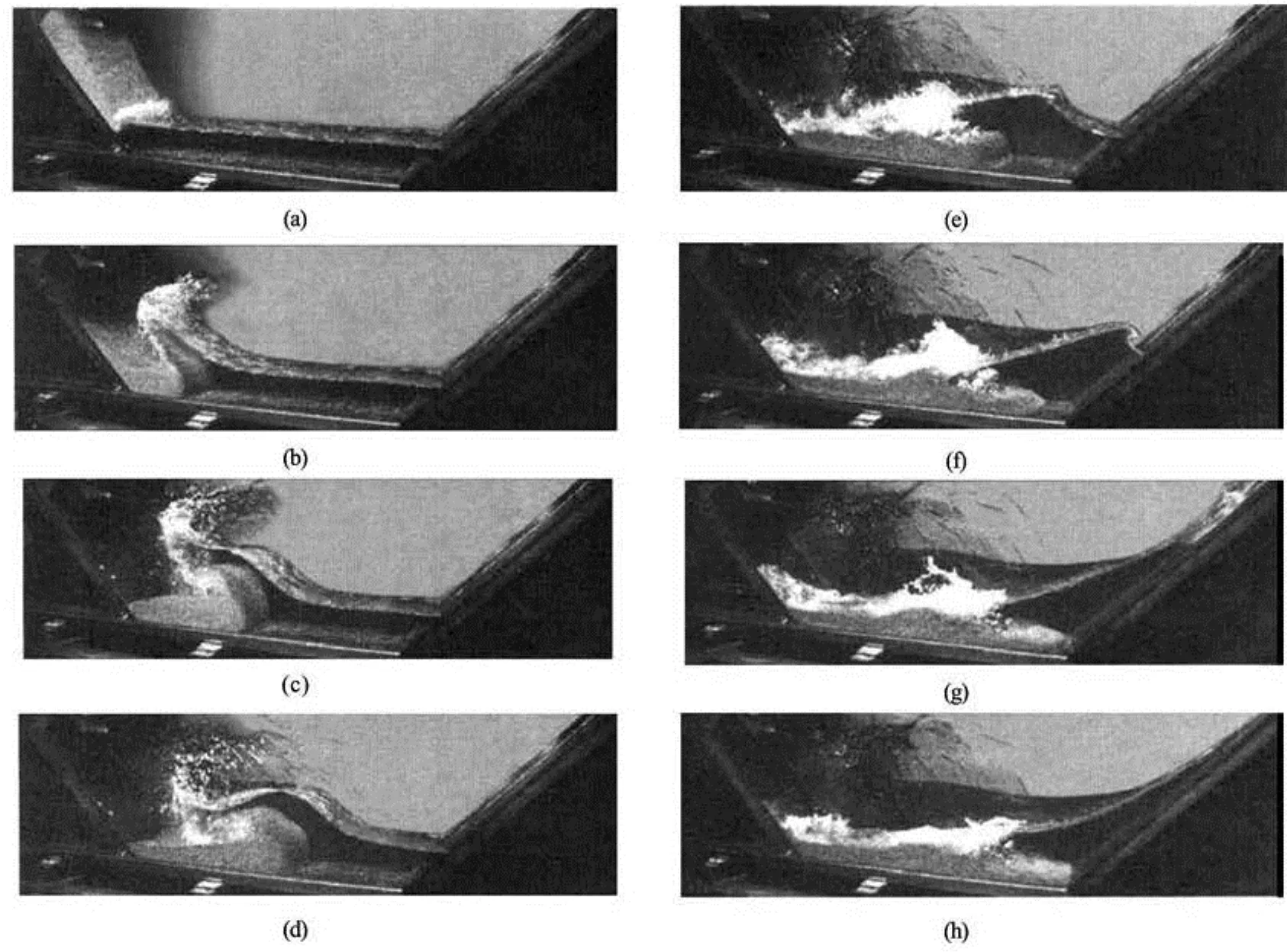
Fig.4 Photo sequence of a granular slide impact experiment at a time increment of 5 s[7]

Lituya Bay is a large inlet on the northeast shore of the Gulf of Alaska. On July 8, 1958, a rockslide volume of about 3×107m3was released on the northeast wall of the Gilbert Inlet up to an elevation of 915 m. The rockslide impacted the water at a high speed creating a giant nonlinear wave with the highest wave runup in the recorded history, and the soliton like wave ran up to an altitude of 524 m causing forest destruction and erosion down to bedrock on a spur ridge, as shown in Fig.2[7].

On the basis of the generalized Froude similarity, Fritz et al.[7]built a 2-D physical model of the Gilbert inlet scaled at 1:675 and the rockslide was modeled with an artificial granular material. Using the present methodology and the numerical model, the density image sequence of the landslide impact is obtained, as shown in Fig.3, while Fig.4 gives the corresponding sequence obtained from the physical model[7]. It is observed that the interfaces between the three fluids are sharp in the physical model, i.e., no mixing occurs during the first moments of the landslide impact, as is also assumed in the numerical model. The simulation predictions of the wave height are qualitatively in good agreement with the experimental results. In both the physical and numerical models, the whole process of a high speed granular slide impact may be subdivided into two main stages: (1) rockslide impact and penetration with flow separation, cavity formation and wave generation, and (2) air cavity collapse with rockslide run-out and debris detrainment causing massive phase mixing.

From the present simulation, after 9.1 s of sliding, the slide begins to impact the water with a velocity of about 72 m/s (Fig.3(a)). The impact continues and the penetration begins to occur followed by the slide bulking caused by the impact on the water surface and the deflection at the channel bottom (Fig.3(b)). The flow separation on the rockslide shoulder occurs due to the fast slide penetration into the water body where the energy is transferred from the landslide to the water (Fig.3(c)). A large air cavity is created on the back of the granular slide where the slide penetration velocity exceeds the wave propagation velocity. (Figs.3(d)-3(f)). The air cavity subsequently collapses during the slide run-out along the bottom causing a significant air-water mixing (Figs.3(g) and3(h)).

It is noted that the wave height is over-predicted when the numerical result is compared with the experiment value. In terms of the maximum runup at the headland, 573 m as given by the current simulation is higher than that observed in the experiment 527 m, which is attributed to the reduced energy dissipation in the numerical model. In fact, the energy losses due to the turbulence and the phase mixing are not considered in the current numerical model. The same point was also reported by Quecedo et al.[8,9]. Generally, theagreement between the current simulation and the experimental data is still good and the basic process of an impulse wave generated by the landslide is captured. Further work may involve a thorough study of different constitutive models of the landslide and its effect on the generated impulse wave.

[1] HELLER V., SPINNEKEN J. Improved landslide-tsunami prediction: Effects of block model parameters and slide model[J].Journal of Geophysical Research: Oceans,2013, 118(3): 1489-1507.

[2] OLSSON E., KREISS G. A conservative level set method for two phase flow[J].Journal of Computational Physics,2005, 210(1): 225-246.

[3] OLSSON E., KREISS G. and ZAHEDI S. A conservative level set method for two phase flow II[J].Journal of Computational Physics,2007, 225(1): 785-807.

[4] BARTO P. T., OBADIA B. and DRIKAKIS D. A conservative level-set based method for compressible solid/ fluid problems on fixed grids[J].Journal of Computational Physics,2011, 230(21): 7867-7890.

[5] OWKES M., DESJARDINS O. A discontinuous Galerkin conservative level set scheme for interface capturing in multiphase flows[J].Journal of Computational Physics,2013, 249(15): 275-302.

[6] CHEN C., LING C. Granular-flow rheology: Role of shear-rate number in transition regime[J].Journal of Engineering Mechanics (ASCE),1996, 122(5): 469-480.

[7] FRITZ H. M., HAGER W. H. and MINOR H. W. Lituya bay case: Rockslide impact and wave run-up[J].Science of Tsunami Hazards,2001, 19(1): 3-23.

[8] QUECEDO M., PASTOR M. and HERREROS M. I. Numerical modeling of impulse wave generated by fast landslides[J].International Journal for Numerical Methods in Engineering,2004, 59(12): 1633-1656.

[9] PASTOR M., HERREROS M. I. and MERODO J. A. F. et al. Modelling of fast catastrophic landslides and impulse waves induced by them in fjords, lakes and reservoirs[J].Engineering Geology,2009, 109(1-2): 124-134.

10.1016/S1001-6058(14)60056-1

* Project supported by the National Natural Science Foundation of China (Grant No. 51279050), the National High Technology Research Development Program of China (863 Program, Grant No. 2012AA112507) and the Non-profit Industry Financial Program of Ministry of Water Resources of China (Grant No. 201301058).

Biography: ZHAO Lan-hao (1980-), Male, Ph. D., Professor

LIU Xiao-qing,

E-mail: lxqhhu@163.com