一類不可微多目標(biāo)分式規(guī)劃問題的最優(yōu)性條件
張曉敏, 吳澤忠
(成都信息工程學(xué)院 數(shù)學(xué)學(xué)院, 四川 成都 610225)
1 預(yù)備知識(shí)
在F-凸[1]和ρ-凸[2]的基礎(chǔ)上,V. Preda[3]提出(F,ρ)-凸的概念,并獲得一些結(jié)果,是F- 凸和ρ- 凸的擴(kuò)展;Z. A. Liang等[4]提出(F,α,ρ,d)- 凸的概念,進(jìn)一步擴(kuò)展了(F,ρ)-凸;文獻(xiàn)[5]在(F,α,ρ,d)-凸的基礎(chǔ)上,提出了廣義(F,α,ρ,d)- 凸的概念.
在不同的凸性假設(shè)下,已得到一些成果[1,3,6-19],但是在微分概念基礎(chǔ)上的非線性規(guī)劃理論和算法不再適用于非光滑最優(yōu)化問題,對(duì)于非光滑最優(yōu)化問題也已得出一些結(jié)論[20-31]. 本文在非光滑(F,α,ρ,d)-凸函數(shù)的基礎(chǔ)上給出廣義非光滑(F,α,ρ,d)- 凸函數(shù)的定義,在這些弱化的凸性的假設(shè)下得出一類不可微多目標(biāo)分式規(guī)劃問題的最優(yōu)性條件.
考慮多目標(biāo)分式規(guī)劃問題(MFP)
其中,fi:Rn→R,gi:Rn→R,i=1,2,…,p,hj:Rn→R,j=1,2,…,m,都是局部Lipschitz函數(shù),并假設(shè)在Rn上,fi(x)≥0,gi(x)>0,i=1,2,…,p.稱S={x∈Rn|hj(x)≤0,j=1,2,…,m}為(MFP)的可行集.
本節(jié)中約定?x,y∈Rn,x>y?xi>yi,i=1,2,…,n;x≥y?xi≥yi,i=1,2,…,n[13].
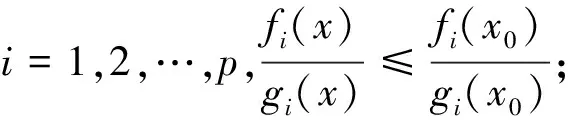
定義3[30]如果f:Rn→R在x∈Rn上是局部Lipschitz函數(shù),則f在x∈Rn沿方向d∈Rn的廣義導(dǎo)數(shù),記為f0(x;d),定義為
定義4[30]設(shè)f:Rn→R是局部Lipschitz函數(shù),f在x∈Rn處的廣義Clarke梯度定義為?f(x),記?f(x)={ξ∈Rn:f0(x;d)≥ξTd,?d∈Rn}.
定義5[30-31]設(shè)f:Rn→R是Lipschitz的,d∈Rn,稱f在x∈Rn處正則,如果f在x∈Rn處是方向可微的,且f0(x;d)=f′(x;d).
定義6[3]稱函數(shù)F:Rn×Rn×Rn→R為次線性函數(shù),如果?x,x0∈X0有
F(x,x0;a1+a2)≤F(x,x0;a1)+
F(x,x0;a2), ?a1,a2∈Rn,
F(x,x0;αa)=αF(x,x0;a),
?α∈R,α≥0, ?a∈Rn.
特別地
F(x,x0;0)=F(x,x0;0a)=0×F(x,x0;a),
0∈R, 0∈Rn, ?a∈Rn.
定義7[29]設(shè)F:Rn×Rn×Rn→R是次線性函數(shù),函數(shù)f:Rn→R在x0∈Rn是局部Lipschitz的,α:Rn×Rn→R+{0},ρ∈R,d:Rn×Rn→R.稱函數(shù)f在x0是非光滑(F,α,ρ,d)-凸函數(shù),如果對(duì)?ξ∈?f(x0),對(duì)所有的x∈Rn有
f(x)-f(x0)≥F(x,x0;α(x,x0)ξ)+ρd2(x,x0).
如果函數(shù)f在Rn上每一點(diǎn)都是非光滑(F,α,ρ,d)-凸函數(shù),則稱f在Rn上是非光滑(F,α,ρ,d)-凸函數(shù).
定義8如果f(x) 定義9如果f(x)≤f(x0)?F(x,x0;α(x,x0)ξ)≤-ρd2(x,x0),則稱f在x0∈X是非光滑強(qiáng)(F,α,ρ,d)-偽凸函數(shù). 定義10如果f(x)≤f(x0)?F(x,x0;α(x,x0)ξ)<-ρd2(x,x0),則稱f在x0∈X是非光滑弱嚴(yán)格(F,α,ρ,d)-偽凸函數(shù). 在點(diǎn)x0∈Rn定義集合J*={j∈J∣hj(x0=0)},J={1,2,…,m}. 約束規(guī)格在點(diǎn)x0,Ω0≠?. 引理1[30]設(shè)f1,f2:Rn→R在x處是Lipschitz的,如果f1(x)≥0,f2(x)>0,f1-f2在x處正則,則 證明由f-vge:=(f1-v1g1,…,fp-vpgp)在x0∈X是非光滑(F,α,ρ,d)-偽凸函數(shù)得 fi(x)-vigi(x) 又由τ>0,αi(x,x0)>0, ? ? 定理2設(shè)(x0,τ,λ)∈Rn×Rp×Rm滿足 λjhj(x0)=0,j=1,2,…,m, (2) τ>0,λ≥0, (3) 對(duì)所有的i=1,2,…,p,fi(x)-vigi(x)≤fi(x0)-vigi(x0); 對(duì)其中某些k,fi(x)-vigi(x) (5) 又h在x0∈X是非光滑(F,α″,ρ″,d″)-凸函數(shù),有 (6) 所以 (7) (7)+(8)式得 即 那么x0是(MFP)的有效解. 證明只需改變定理2的證明中的關(guān)于函數(shù)h的部分. 由h在x0∈X是非光滑(F,α″,ρ″,d″)-偽凸函數(shù)(或非光滑弱嚴(yán)格(F,α″,ρ″,d″)-偽凸函數(shù)),及hj(x)≤0,hj(x0)=0得hj(x)≤hj(x0),故 即(6)式,余下證明與定理2相同. (9) 如果fi、-gi(i=1,…,p)在x0是非光滑(F,α1i,ρ1i,d1i)-凸函數(shù),hj(j=1,…,m)在x0是非光滑強(qiáng)(F,α2j,ρ2j,d2j)-偽凸函數(shù),且 (11) 假設(shè)x0不是(MFP)的有效解,則存在(MFP)的有效解x使得 至少有一個(gè)不等式嚴(yán)格成立. 至少有一個(gè)不等式嚴(yán)格成立. 又τ>0,所以 由F的次線性性得 由hj(j=1,…,m)在x0是非光滑強(qiáng)(F,α2j,ρ2j,d2j)-偽凸函數(shù),及hj(x)≤0,hj(x0)=0,有hj(x)≤hj(x0),故 又λj≥0,α2j(x,x0)>0及F的次線性性可得 即 (12)+(13)式得 顯然與(10)式矛盾. 證明只需改變定理4證明中的關(guān)于函數(shù)h的部分. 由hj(j=1,…,m)在x0是非光滑弱嚴(yán)格(F,α2j,ρ2j,d2j)-偽凸函數(shù),及hj(x)≤0,hj(x0)=0,有hj(x)≤hj(x0),故 又λj≥0,α2j(x,x0)>0及F的次線性性可得 即得(13)式,其余部分的證明與定理4相同. 致謝成都信息工程學(xué)院引進(jìn)人才項(xiàng)目(KYTZ201203)和成都信息工程學(xué)院中青年學(xué)術(shù)帶頭人科研基金(J201218)對(duì)本文給予了資助,謹(jǐn)致謝意. [1] Gulati T R, Islam M A. Sufficiency and duality in multi-objective programming problems involving generalizedF-convex functions[J]. J Math Anal Appl,1994,183:181-195. [2] Vial J P. Strong and weak convexity set and functions[J]. Math Oper Res,1983,8:231-259. [3] Preda V. On efficiency and duality for multi-objective programs[J]. JMAA,1992,166:365-377. [4] Liang Z A, Huang H X, Pardalos P M. Optimality conditions and duality for a class of nonlinear fractional programming problems[J].J Opt Theory Appl,2001,110:611-619. [5] 吳澤忠,李澤民. 廣義(F,α,ρ,d)-凸條件下多目標(biāo)規(guī)劃問題的最優(yōu)性充分條件[J]. 經(jīng)濟(jì)數(shù)學(xué),2002,19(4):90-94. [6] Weir T , Mond B. Generalized convexity and duality in multi-objective programming[J]. Bull Austral Math Soc,1989,39:287-299. [7] Egudo R. Efficiency and generalized convex duality for multi-objective programs [J]. J Math Anal Appl,1989,138:84-94. [8] 曾德勝,吳澤忠. 一類多目標(biāo)分式規(guī)劃問題的最優(yōu)性條件[J]. 四川大學(xué)學(xué)報(bào):自然科學(xué)版,2006,43(4):751-756. [9] 吳澤忠,鄭豐華. 一類非線性分式規(guī)劃問題的最優(yōu)性條件和對(duì)偶[J]. 四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2007,30(5):594-597. [10] 吳傳平. 多目標(biāo)數(shù)學(xué)規(guī)劃解的一些新的充要條件[J]. 重慶文理學(xué)院學(xué)報(bào):自然科學(xué)版,2011,30(4):9-11. [11] 李瑞華,主雪梅. 廣義凸規(guī)劃問題的最優(yōu)性條件[J]. 綿陽師范學(xué)院學(xué)報(bào):自然科學(xué)版,2010,2(29):15-18. [12] 李動(dòng)鋒,邱根勝. 一種新廣義凸多目標(biāo)分式規(guī)劃的最優(yōu)性充分條件[J]. 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2009,25(4):807-815. [13] 彭再云,雷鳴,劉亞威,等. 一類可微凸多目標(biāo)分式規(guī)劃的最優(yōu)性條件[J]. 重慶交通大學(xué)學(xué)報(bào):自然科學(xué)版,2009,28(1):156-158. [14] 吳澤忠. (F,α,ρ,d)-凸性下一類多目標(biāo)分式規(guī)劃問題的最優(yōu)性條件和對(duì)偶[J]. 四川大學(xué)學(xué)報(bào):自然科學(xué)版,2009,46(6):1623-1627. [15] 江維瓊,吳春. 廣義(F,α,ρ,d)-凸性條件下多目標(biāo)分式規(guī)劃問題的K-T條件及對(duì)偶[J]. 黃岡師范學(xué)院學(xué)報(bào),2006,26(3):11-27. [16] Cambini A, Martein L. Generalized Convexity and Optimization[M]. Berlin,Heideberg:Spriner-Verlag,2008:78-81. [17] 林銼云,董加禮. 多目標(biāo)優(yōu)化的方法與理論[M]. 長(zhǎng)春:吉林教育出版社,1992:1-449. [18] 曾德勝,吳澤忠. (F,α,ρ,d)-凸和廣義(F,α,ρ,d)-凸性下一類多目標(biāo)規(guī)劃問題的對(duì)偶[J]. 四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2006,29(1):63-66. [19] 張曉敏,吳澤忠. (F,α,ρ,d)-凸和廣義(F,α,ρ,d)-凸條件下一類多目標(biāo)規(guī)劃問題的對(duì)偶[J]. 成都信息工程學(xué)院學(xué)報(bào),2012,27(3):318-325. [20] Liu J C. Optimality and duality for generalized fractional programming involving nonsmooth (F,P)-convex functions[J]. Comput Math Appl,1996,32:91-102. [21] 羅勇,姚元金. 一類非凸非光滑多目標(biāo)分式規(guī)劃的最優(yōu)性條件[J]. 湖北民族學(xué)院學(xué)報(bào):自然科學(xué)版,2009,27(4):398-402. [22] 顏麗佳. 非光滑(F,α,ρ,d)-凸函數(shù)的多目標(biāo)分式規(guī)劃最優(yōu)性條件[J]. 西華師范大學(xué)學(xué)報(bào):自然科學(xué)版,2006,27(4):361-364. [23] 顏麗佳. 關(guān)于非光滑(F,α,ρ,d)-凸函數(shù)的多目標(biāo)分式規(guī)劃的對(duì)偶性[J]. 西華師范大學(xué)學(xué)報(bào):自然科學(xué)版,2008,29(1):24-28. [24] Zhao K Q, Tang L P, Yang X M. Optimality and duality for a class of non-smooth optimization problems[J]. OR Transactions,2010,14(2):45-54. [25] 趙克全,唐莉萍. 一類不可微多目標(biāo)分式規(guī)劃問題的最優(yōu)性條件[J]. 重慶師范大學(xué)學(xué)報(bào):自然科學(xué)版,2010,27(4):1-4. [26] 唐莉萍,蔣華, 趙克全,等. 一類非光滑規(guī)劃問題的混合對(duì)偶[J]. 四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2011,34(1):34-37. [27] Zheng X J, Cheng L. Minimax fractional programming under non-smooth generalized (s,ρ,θ) -d-univexity[J]. J Math Anal Appl,2007,328:676-689. [28] 姜艷,張慶祥. 一類不可微凸多目標(biāo)規(guī)劃解的最優(yōu)性充分條件[J]. 延安大學(xué)學(xué)報(bào):自然科學(xué)版,2010,29(1):17-21. [29] Liu S M, Feng E M. Optimality conditions and duality for a class of nondifferentiable multi-objective fractional programming problems[J]. J Glob Optim,2007,38:653-666. [30] Clarke F H. Optimization and Nonsmooth Analysis[M]. New York:Wiley-Interscience,1983. [31] 趙克全,羅杰,唐莉萍. 一類非光滑規(guī)劃問題的最優(yōu)性條件[J]. 重慶師范大學(xué)學(xué)報(bào):自然科學(xué)版,2010,27(2):1-3.2 最優(yōu)性條件
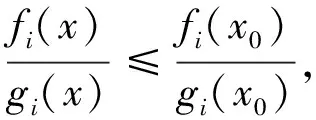
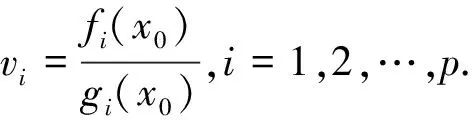
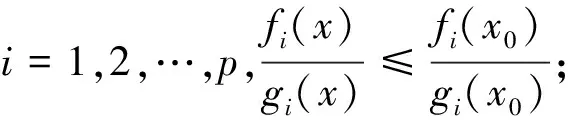
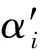
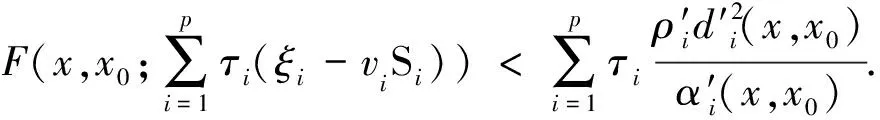
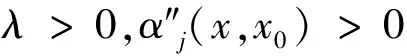
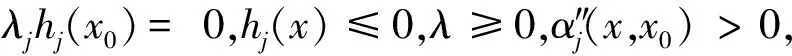
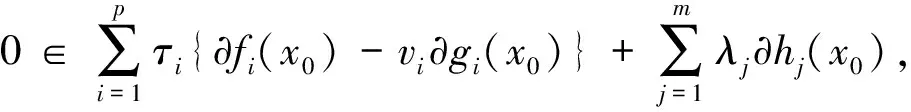

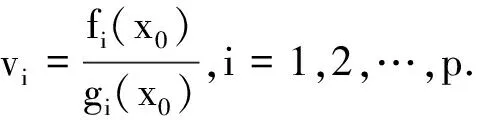
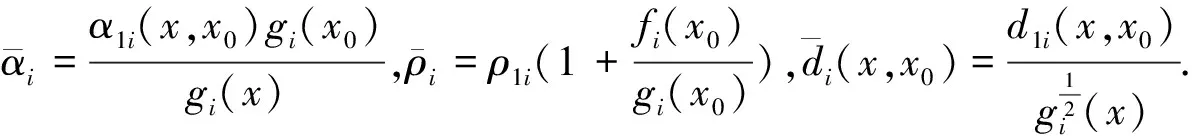
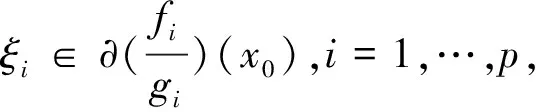
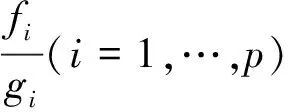
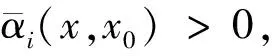

 四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2014年3期
四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2014年3期
——基于1986-2009年的數(shù)據(jù)
