Haneul Yoon, Sukhee Park, Sangyong Lee, Jangmyung Lee

(Department of Electrical Engineering, Pusan National University, Pusan 609-735, Korea)

Study on denoising filter of underwater vehicle using DWT*

Haneul Yoon, Sukhee Park, Sangyong Lee, Jangmyung Lee

(Department of Electrical Engineering, Pusan National University, Pusan 609-735, Korea)

In the step processing a digitalized signal, noises are generated by internal or external causes of the system. In order to eliminate these noises, various methods are researched. Among these noise elimination methods, Fourier fast transform (FFT) and short-time Fourier transform (STFT) are widely used. Because they are expressed as a fixed time-frequency domain, they have the disadvantage that the time information about the signal is unknown. In order to overcome these limitations, by using the wavelet transform that provides a variety of time-frequency resolution, multi-resolution analysis can be analysed and a varying noise depending on the time characteristics can be removed more efficiently. Therefore, in this paper, a denoising method of underwater vehicle using discrete wavelet transform (DWT) is proposed.

discrete wavelet transform(DWT); denoising filter; underwater vehicle; digital signal processing

0 Introduction

Noise in the process of acquiring and processing a signal is caused by various reasons, which decreases the accuracy of the signal and generates a fatal error in the process of transmitting and receiving data. Because the amount of calculation is less, a method of applying the most common digital filter algorithm has been applied extensively. However, this method generates errors when the frequency gets out of the normal value. For these disadvantages, some adaptative techniques based on feedback loop have been proposed by recursive orthogonal filter with accurate gain, variable data window and adjustment of sampling interval. Also, the non-linear curve approximation techniques, including repeated least square algorithm[1]and extended Kalman filter[2]based on a fixed signal model were utilized in the fundamental frequency estimation. The accuracy of this method was limited only within narrow range in around regular frequency because of Taylor expansion of the non-linear cycle. Artificial intelligence techniques, such as neural network[3]and genetic algorithm[4], can be used to achieve accurate frequency estimation extensively in a quick response. These optimization techniques have excellent performance, but real-time implementation is not easy because of the number of complex calculation.

For this reason, when measuring the signal's change due to velocity's change of the vehicle, the existing research on real-time implementation is used in low-pass filter and high-pass filter with a particular band for filtering. However, the results cause the distortion of the signal when filtering a signal corresponding to a change in speed[5].

Recently, the wavelet theory has been used as a useful mathematical tool for practical applications in various fields. Among these applications, many studies on wavelet-based technique for de-noising have been done in recent years[6-8]. A de-noising method using wavelet theory takes wavelet coefficients by performing the discrete wavelet transform (DWT) on the measured signal and applies the appropriate threshold values for these coefficients.

If the coefficient is smaller than threshold value, it may be caused by noise. If the coefficient is greater than threshold value, it may be caused by original signal. By taking inverse discrete wavelet transform (IDWT) from the wavelet coefficients, it is possible to obtain a de-noising signal. The methods of applying the threshold value are soft and hard threshold processing methods proposed by Donoho, et al.[9,10]. Also, using the wavelet transform (multi-resolution) can avoid falling into regional solutions[6].

Therefore, in this paper, in order to reduce the noise of the measured signal in real time and filter signal according to the change of velocity of underwater vehicle, DWT is applied to actively reduce and expand time-domain and frequency-domain information.

Firstly, we will introduce DWT in section 1. In section 2, we describe the de-noising method of underwater vehicle using DWT and verify it through experiments in section 3, and give a conclusion in section 4.

1 Discrete wavelet transform

The wavelet transform is being well used along with fast Fourier transform (FFT) and short-time Fourier transform (STFT) in the field of signal processing. Above all, FFT is used in signal processing and the solutions of differential equations. In addition, FFT only analyzes the frequency domain. Therefore, FFT has the disadvantage in that it needs to determine the time and frequency information of a signal simultaneously[11]. The STFT combines together with a weight function depending on time called windows function and Fourier building blocks are introduced to overcome these limitations. Because STFT is used by attaching a weight function to Fourier transform, it cannot efficiently analyze the non-stationary signal as stochastic characteristics change according to the change in time. The wavelet transform is more efficient than STFT because it uses the mother wavelet as a building block which is the function generated from the result of movement after configuring the scale of the expansion or contraction without a window function to overcome weakness[11].

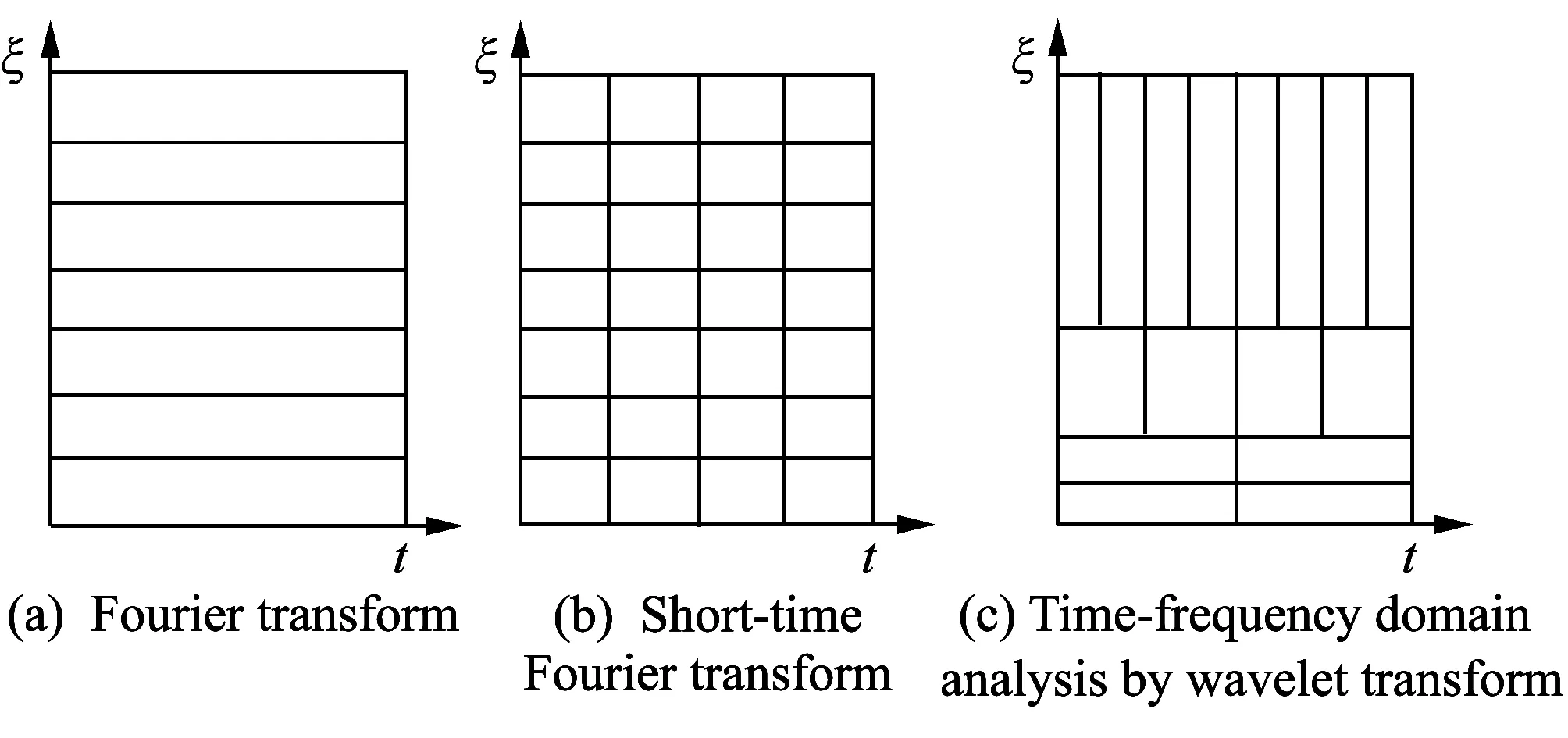
Fig.1 Comparison of FT, STFT and wavelet transform

Using wavelet of which size changes according to compressibility coefficient a to analyze the signal f(t), wavelet transform separates specific components (corresponding to the size of wavelet and a partial size of signal) from the signal and then expressed in time-scale space. In other words, when original signal is expressed by using the basis function of finite length, the set of appropriate signal is decided and then a given signal is reconstructed by using the basis signal or building block.

The basis of the vector v is the set of independent vectors. The basis of vector v can be used as a linear combination of basis vectors. One of the vector spaces forms more of the basis.

On the other hand, they have an equal number of vectors, which is known as the dimension of vector space,

(1)

Eq.(1) shows not only how to use the vector as the linear combination of the basis vector v, but also how to use the response coefficient Vk. This concept can be generalized by replacing basis vector bkhaving basis functions φk(t) with vector v having the function. Therefore, Eq.(1) can be transformed to

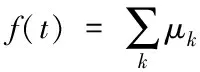
(2)

Assume that there are two functions f(t) and g(t) in L2∈[a,b]. The inner product of two functions is defined as

(3)

According to Eq.(3), the wavelet transform can become the basis function of Ψ(τ,s), namely,

(4)

(5)

Eq.(4) is the basis wavelet transform equation and Eq.(5) is the functional formula of wavelet. Function ψ is the mother wavelet. Extension and contraction are possible by the compressibility coefficient a, and the moving is possible by the transfer coefficient b[7,8,13].

DWT reduces the calculation time fully and provides sufficient information to analyze and combine the original signal in comparison with the basic wavelet transforms. The wavelet transform is calculated by shifting the window according to temporal change, multiplying the signal, and integrating over all time depending on the change in the scale of the analysis windows.

Differently, in case of discrete wavelet, filters of the cut frequency are used to analyze the signal in the different scale. The resolution of the signal that measures the amount of detailed information of signal varies depending on the filtering, and the scale changes according to up-sampling and down-sampling (or subsampling). The down-sampling of signal is the decreasing of sampling ratio or elimination of the optional sample of signal. The up-sampling of signal is the increasing of sampling ratio by adding new sample to the signal. In other words, DWT provides multi-resolution analysis that interprets the original signal using multi-resolution until getting the desired resolution from a low resolution. There is very close relationship for reconstruction of the bands signal based on the filter bank.

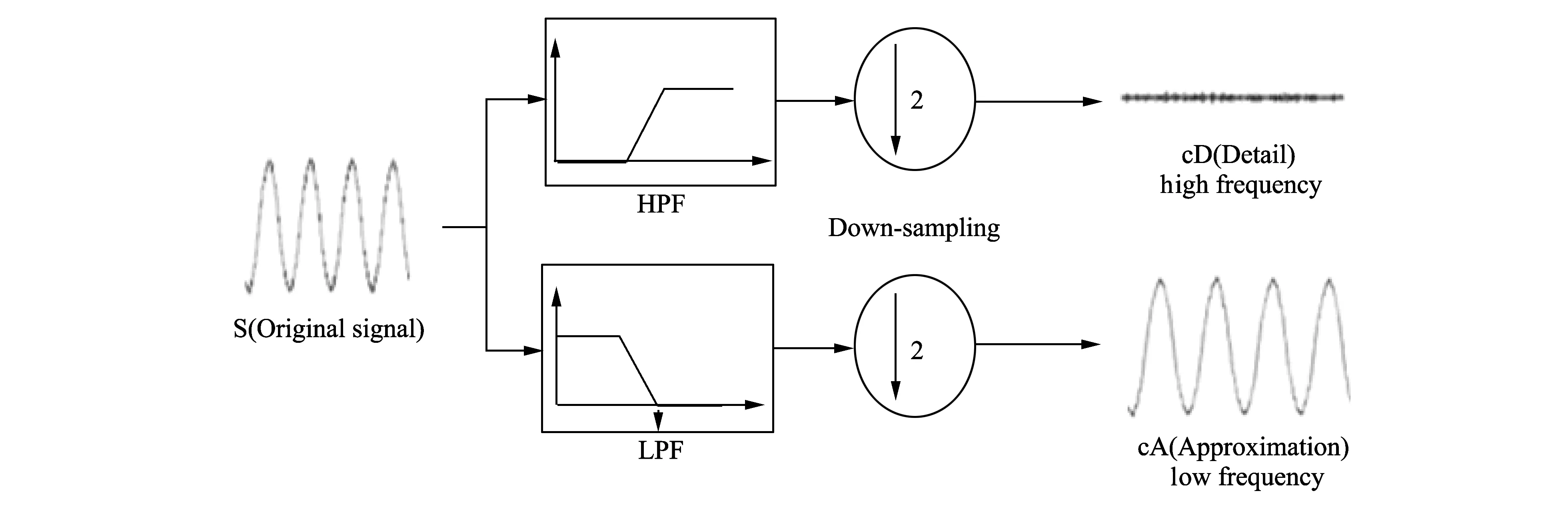
Fig.2 Multi-resolution analysis

Multi-resolution analysis can divide original signal into approximation that is low-frequency components and detail which is high-frequency components. This process can be extended by the concept of two filterings using low-pass filter (LPF) and high-pass filter (HPF) simultaneously.

For the following Eq.(6), f can be expressed by only the wavelet within the range of -∞lt;tlt;∞. By writing series expansion form, Eq.(6) can be expressed by the double summation according to the index (j) expressing scale and (k) representing parallel transference, that is

(6)

In Eq.(6), 〈f,ψj,k〉 means the inner product of f and ψj,k. By utilizing the concept of multi-resolution analysis, wavelet ψ(t) in Eq.(6) obtains Eq.(7) from scaling function y(t). Also, among the scaling functions, it can be seen that there is a relationship with a function such as a wavelet function of Eq.(8)[7-8,13].

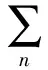
(7)

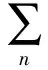
(8)

where hnis the LPF in Eq.(7) and gnis the HPF in Eq.(8). The relationship of hnand gnis

gn(L-1-n)=(-1)nhn(n),

(9)

where L is the length of filter(number of points). Two filters are the inverse version crossing each other with odd index. The change from LPF to HPF is provided through (-1)n.

The very uncertain frequency bands(for example, noise) in original signal have a very small amplitude. So, through the DWT, noise is filtered without loss of the important information.

2 Sensor data filtering using DWT

The intertial navigation system (INS) is quite sensitive to external vibrations or shock. The data of INS sensor can be affected by noise due to the effect of waves on the surface, tidal current and sea breezes. So more noises are added to INS sensor in comparison with the in-ground.

These noises can be removed after analysis of the signal by using a DWT and eliminating analyzed noise depending on its speed through variable threshold method (VTM). With VTM, the wavelet coefficient will converge to zero if it does not reach the threshold value. VTM performs the thresholding by using the soft threshold which is the same as[10,13]

(10)

In Eq.(10), u means the wavelet coefficients calculated by performing DWT. How to set the basis value of λ is one of the important factors affecting the performance of the VTM. Generally, the basis value of λ is determined by Eq.(10). Otherwise, the value of λ determined by Eq.(10) does not produce the best results. Therefore, it determines λ experimentally as

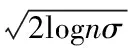
(11)

In Eq.(11), σ is the standard deviation of the signal and n is the sampling number of the signal[10,13].

Therefore, the VTM has the advantage of removing noise by decomposing the high frequency and low frequency components. And it is to minimize the distortion of the signal.

Fig.3 presents the block diagram of the de-noising of the accelerometer sensor using DWT and VTM.

Fig.3 Denoising of sensor data using DWT and VTM

3 Simulation and results

In this paper, we propose de-noising filter algorithm using DWT for active filtering and reducing the noise of the measured signal in real time.

The acceleration data, which includes the most noise and is influenced by the fewest disturbance, is determined according to the results of comparing data of the acceleration, gyro, magnetic compass on the ground/surface for the performance evaluation[14].

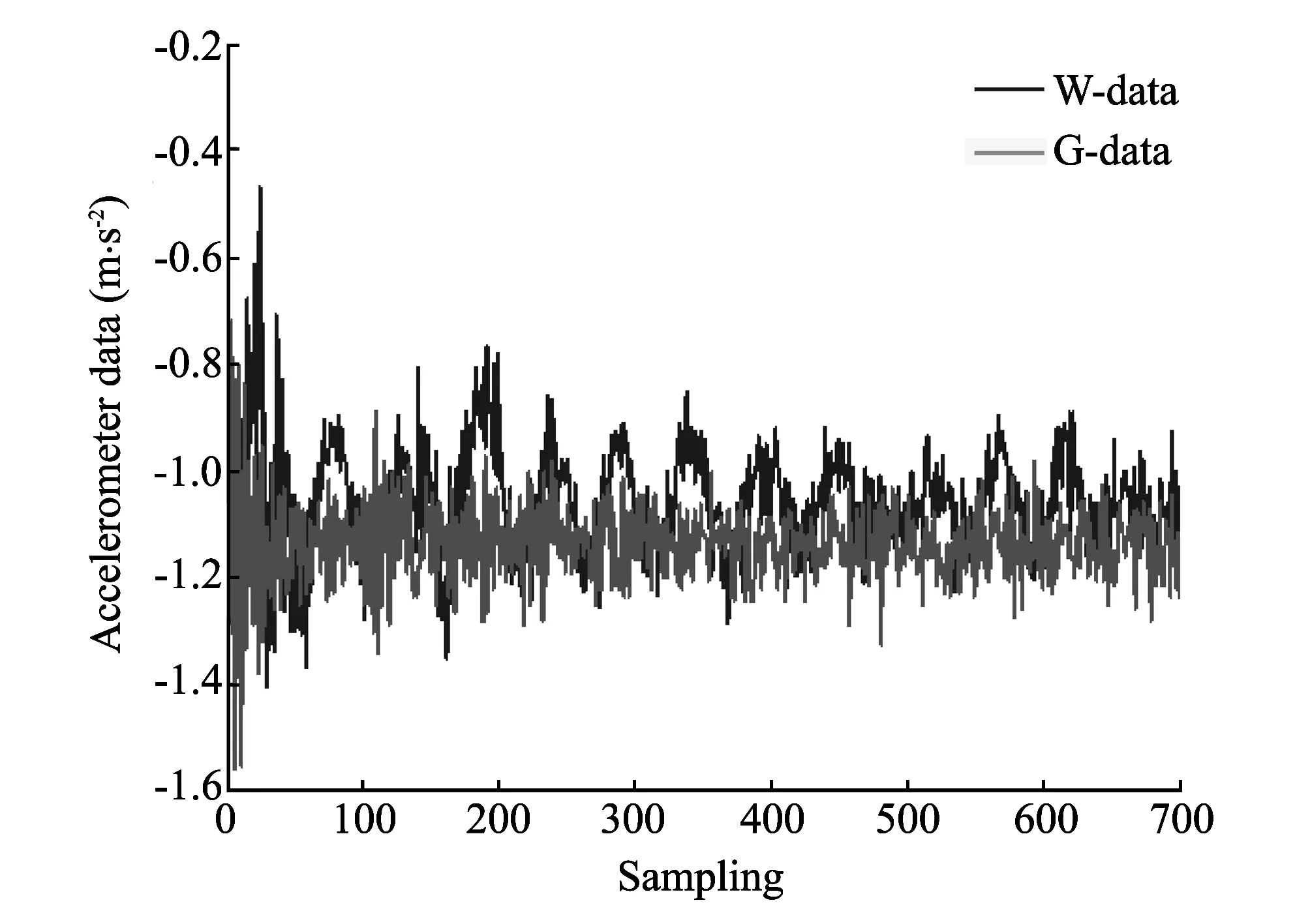
Fig.4 Comparison of acceleration data in ground/water

Therefore, the added noise will be eliminated by applying it to acceleration with de-noising filter using 1-3 level DWT, as shown in Fig.5.

Fig.5 Acceleration data applying 1-3 level DWT

In Fig.5, a distortion of the original data happens because of the very higher DWT processing due to increase in DWT's level. It is also anticipated that the computational increases exponentially when using the real-time system.

4 Conclusion

In this paper, we conduct study about de-noising filtering of sensor signal used for underwater vehicle by applying DWT. As shown in the simulation, the noise added to the signal is removed by applying the DWT to the each level. However, if DWT processing is too highly applied to the signal thoughtlessly, the distortion of the original signal will happen. Afterward, by identifying the characteristics of sensor data adding the noise, techniques that can filter actively according to the appropriate level is going to be applied. Research will be proceededes focusing on the vibration of submersible motors according to the velocity of thruster which influences the underwater sensors in order to apply the DWT to the underwater vehicle. Nested disturbances are different from the velocity. Therefore, the characteristics of each noise are analysed after signal is separated in the several scale domain by using DWT. Then the controller will be designed to modulate DWT’s level actively according to change in disturbance.

[1] Ku K J, Cho B H, Lee D S. A study on the degign of two-dimensional FIR digital filters using least-square error algorithm. The Institute of Electronics Engineers of Korea, 1988, 25(7): 285-289.

[2] Kang B S, Yeo G H. A study on development of a reconfigurable mobile robot and dead-reckoning using extended Kalman filter. The Korean Society of Mechanical Engineers, 2009, 33(5): 455-462.

[3] Lai L L, Chen W L, Tse C T, et al. Real time frequency and harmonic evaluation using artificial networks. IEEE Transactions on Power Delivery, 1999, 14(1): 52-57.

[4] EL-Naggar K M, Youssef H K M. A generic based algorithm for frequency relaying applications. Electric Power Systems Research, 2000, 55(3): 173-178.

[5] Seo W K, Lee J M. Precise outdoor localization of a GPS-INS integration system using discrete wavelet transforms and unscented particle filter. The Institute of Electronics Engineers of Korea, 2011, 48(11): 82-90.

[6] Szu H H, Telfer B A, Kadambe S L. Neural network adaptive wavelets for signal representation and classification. Optical Engineering, 1992, 31(9): 1907-1916.

[7] Lee S H, Yoon D H. Wavelet transform (well defined), 2nd Ed. Jinhan Books, Korean, 2003.

[8] Kang H B. Wavelet theory and its applications. Acanet, Korea, 2001.

[9] Donoho D L, Johnstone J M. Ideal spatial adaptation by wavelet shrinkage. Biometrika, 1994, 81(8): 425-455.

[10] Donoho D L. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 1995, 41(5): 613-627.

[11] Groves P D, Handley R J, Runnalls A R. Optimizing the integration of terrain referenced navigation with INS and GPS. Robotica, 2006, 59(1): 71-89.

[12] XU Yan-sun, Weaver J B, Healy D M Jr., et al. Wavelet transform domain filters : a spatially selective noise filtration technique. IEEE Transactions on Image Processing, 1994, 3(6): 747-758.

[13] LIU Gang, QU Liang-sheng. Study on wavelet adaptive-threshold denoising method. Signal Processing, 2002, 18(6): 509-512.

[14] Yoon B D, Yoon H N, Choi S H, et al. Estimated position of sea-surface beacon using DWT/UKF. Institute of Control, Robotics and Systems, 2013, 19(4): 341-348.

date： 2013-04-17

Haneul Yoon (haneul1696@pusan.ac.kr)

CLD number： TN911.7 Document code： A

1674-8042(2013)03-0238-05

10.3969/j.issn.1674-8042.2013.03.008