光場(chǎng)位相算符和逆算符的Weyl編序展開*
李學(xué)超 楊陽(yáng) 范洪義
1)(安徽理工大學(xué)理學(xué)院,淮南 232001)
2)(中國(guó)科學(xué)技術(shù)大學(xué)近代物理系,合肥 230026)
3)(中國(guó)科學(xué)技術(shù)大學(xué)材料科學(xué)與工程系,合肥 230026)
(2012年9月2日收到;2012年12月26日收到修改稿)
1 引言
自從1927年Dirac[1]首次通過(guò)光子湮滅算符引入位相算符以來(lái),在量子光學(xué)中它一直是個(gè)重要的課題.在量子力學(xué)中位相算符可以反映量子態(tài)的位相性質(zhì),Dirac通過(guò)極分解a=·S(S為位相算符)定義位相算符,這里N=a?a是[粒子]數(shù)算符,a?(a)分別是玻色產(chǎn)生 (湮滅)算符,a,a?=1.隨后Carruthers等[2]修正了位相算符,把它定義為

那么位相算符的經(jīng)典對(duì)應(yīng)是什么?這個(gè)問(wèn)題的解決在以往的文獻(xiàn)中尚未見有討論,原因可能是位相算符是非線性的.本文通過(guò)推導(dǎo)位相算符的Weyl編序來(lái)研究它及其經(jīng)典對(duì)應(yīng),在此基礎(chǔ)上研究產(chǎn)生算符和湮滅算符的逆的Weyl編序.這是深入了解光場(chǎng)算符性質(zhì)的一種新的途徑.
在粒子數(shù)表象|n〉中,利用


得到位相算符在粒子數(shù)表象中展開

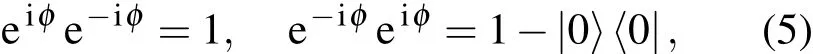
注意到|0〉是真空態(tài),a|0〉=0,可見 eiφ與 e-iφ是不對(duì)易的.
在量子光學(xué)中,人們經(jīng)常會(huì)將算符在不同的表象中展開,如P表示,Q表示以及密度算符的Wigner函數(shù)[3-6]等.算符A的Q表示可以簡(jiǎn)單地利用粒子數(shù)表象來(lái)獲得:

在以往的文獻(xiàn)中,方程(6)除了提示我們求矩陣元Am,n外,并沒(méi)有提供過(guò)多的信息,|m〉〈n|被認(rèn)定是這種展開的一個(gè)“終極的”表示.本文將突破|m〉〈n|這個(gè)“終極的”表式,用算符的Weyl編序理論對(duì)上式繼續(xù)推導(dǎo),將A以Weyl編序展開[7].利用Weyl編序算符在相似變換下的序不變的優(yōu)點(diǎn),不僅可以獲得關(guān)于光場(chǎng)算符的一些新的信息,同時(shí)也推導(dǎo)出許多有用的積分公式和一些特殊函數(shù)的生成函數(shù),尤其是導(dǎo)出帶負(fù)冪次的復(fù)高斯積分公式.
2 |m>文獻(xiàn)[8]曾導(dǎo)出任意一個(gè)算符的Weyl編序形式的公式


可見(7)式是正確的.由

并且利用雙變量厄米特多項(xiàng)式的積分與表示

這里

我們就可用有序算符內(nèi)的積分技術(shù)[9-12]來(lái)推導(dǎo)出|m〉〈n|的 Weyl編序式

將上式代入(7)式,即可得到任一算符用雙變量的厄米特多項(xiàng)式展開的新形式

3 光場(chǎng)位相算符的經(jīng)典對(duì)應(yīng)
作為(13)式的應(yīng)用,我們來(lái)推導(dǎo)位相算符的Weyl編序.利用

將其代入(13)式,得到

根據(jù)Weyl量子化理論[7],位相算符 e-iφ的Weyl對(duì)應(yīng)式為

由于Wigner算符Δ(α)的Weyl編序?yàn)閇13]

所以對(duì)照(15)式可見

這說(shuō)明位相算符的經(jīng)典對(duì)應(yīng)是

可見位相算符 e-iφ對(duì)應(yīng)的經(jīng)典位相體現(xiàn)在 eiφ,
同樣我們也可以算出 eiφ的Weyl編序式

所以算符 eiφ的經(jīng)典對(duì)應(yīng)為

4 產(chǎn)生算符和湮滅算符的逆的Weyl編序式及應(yīng)用
Dirac[14]首先考慮了湮滅算符的逆a-1.既然產(chǎn)生算符描述光子產(chǎn)生過(guò)程,產(chǎn)生算符的逆應(yīng)該描寫光子湮滅過(guò)程;反之,湮滅算符的逆應(yīng)該描寫產(chǎn)生過(guò)程.但要注意由于a|0〉=0,盡管aa-1=1,但a-1a/=1.用相干態(tài)和圍道積分的方法[15]可以將粒子數(shù)態(tài)|n〉表示為

這里的圍道C包括了z=0點(diǎn),在圍道積分下a-1e z a?|0〉=z-1ez a?|0〉就有了意義,于是有

即

a-1滿足

利用(24)式得到

將

代入(13)式得到

另一方面,直接利用(7)式又有

該式代入時(shí)利用了 a-1|β〉=β-1|β〉,比較 (28)和(29)兩式得到

由于Weyl編序中,產(chǎn)生算符與湮滅算符是可交換的,可以將其看作積分參量,從(30)式得到一個(gè)新的積分公式
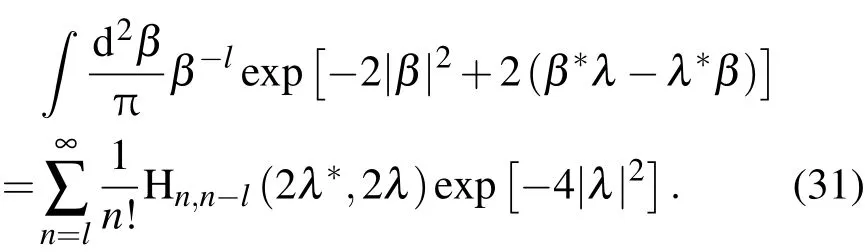
注意β-l是負(fù)冪次,所以這個(gè)積分帶有瑕點(diǎn),不易用常規(guī)的方法積分,這里用Weyl編序方法繞過(guò)了這一困難.()
同樣我們可以推導(dǎo)出a?-l的Weyl編序

由此可以悟出帶負(fù)冪次(β?)-l的新高斯積分公式

進(jìn)一步由(24)式可見

將

代入(13)式得

另一方面,直接利用(7)式又得到

比較以上兩式,可以悟出關(guān)于帶負(fù)冪次(β?)-kβ-l的新高∫斯 積分公式

進(jìn)一步可改寫為

作為比較,我們推導(dǎo)帶正冪次(β?)kβl的新高斯積分公式.將


另一方面,將(a?)kal直接代入(7)式得

比較以上兩式,可以悟出關(guān)于帶正冪次(β?)kβl的新積分公式

另一方面利用(10)式得到

比較(44)與(45)式,得出關(guān)于雙變量厄米特多項(xiàng)式的一個(gè)新的母函數(shù)公式
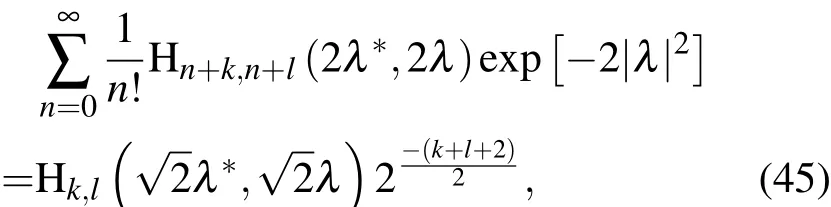
該式也可利用其他方法驗(yàn)證.
(45)式進(jìn)一步可改寫為

該式正好與(41)式相匹配.
5 結(jié)論
本文推導(dǎo)出了光場(chǎng)位相算符的Weyl編序,寫出了其經(jīng)典對(duì)應(yīng),這對(duì)于深入了解光場(chǎng)算符的性質(zhì)提供了一種新的途徑;推導(dǎo)了產(chǎn)生算符與湮滅算符的逆的Weyl編序,并據(jù)此推導(dǎo)出了某些特殊函數(shù)的新的生成函數(shù)和帶負(fù)次冪的高斯積分公式.
[1]Dirac PA M 1927 Proc.R.Soc.London A 114 243
[2]Carruthers P,Nieto M M 1968 Rev.Mod.Phys.40 411
[3]Wigner EP1932 Phys.Rev.40 749
[4]Klauder JR,Skagerstam B S1985 Coherent States(Singerpore:World Scientifi c Publishing)
[5]Scully M O,Zubairy M S 1997 Quantum Optics(United Kingdom:Cambridge University Press)
[6]Glauber RJ1963 Phys.Rev.130 2529
[7]Weyl H 1927 Z.Phys.A 46 1
[8]Fan HY 1992 J.Phys.A 25 3443
[9]Fan H Y,Hu L Y 2008 Chin.Phys.B 17 1640
[10]Yuan H C,Xu X X 2010 Acta Phys.Sin.61 064205(in Chinese)[袁洪春,徐學(xué)翔2012物理學(xué)報(bào)61 064205]
[11]Fan H Y 2008 Ann.Phys.323 1502
[12]Jiang N Q,Fan H Y,Hu L Y 2011 J.Phys.A:Math.Theor.44 195302
[13]Xu X X,Yuan H C,Hu L Y 2010 Acta Phys.Sin.59 4661(in Chinese)[徐學(xué)翔,袁洪春,胡利云2010物理學(xué)報(bào)59 4661]
[14]Dirac P A M 1966 Lectures on Quantum Field Theory(New York:Academic)
[15]Fan H Y 1993 Phys.Rev.A 47 4521
猜你喜歡
利用min{a,b}的積分表示解決一類絕對(duì)值不等式中等數(shù)學(xué)(2022年2期)2022-06-05 07:10:50 利用倒推破難點(diǎn)中學(xué)生數(shù)理化·七年級(jí)數(shù)學(xué)人教版(2021年11期)2021-12-06 05:38:48 如何利用基本不等式比較大小中學(xué)生數(shù)理化(高中版.高考數(shù)學(xué))(2021年6期)2021-07-28 06:19:08 利用一半進(jìn)行移多補(bǔ)少小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2020年6期)2020-07-25 02:31:36 利用口訣算除法小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2019年11期)2019-11-25 07:31:44 利用數(shù)的分解來(lái)思考小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2018年9期)2018-09-26 05:59:44 Roommate is necessary when far away from home瘋狂英語(yǔ)·新讀寫(2018年2期)2018-09-07 09:32:10 利用數(shù)學(xué)小靈通·3-4年級(jí)(2017年6期)2017-06-22 11:28:50 回收木再利用——Piet Hein Eek工業(yè)設(shè)計(jì)(2016年5期)2016-05-04 04:00:33 低丘緩坡未利用地的開發(fā)利用探討河北遙感(2015年4期)2015-07-18 11:05:06
文獻(xiàn)[8]曾導(dǎo)出任意一個(gè)算符的Weyl編序形式的公式


可見(7)式是正確的.由

并且利用雙變量厄米特多項(xiàng)式的積分與表示

這里

我們就可用有序算符內(nèi)的積分技術(shù)[9-12]來(lái)推導(dǎo)出|m〉〈n|的 Weyl編序式

將上式代入(7)式,即可得到任一算符用雙變量的厄米特多項(xiàng)式展開的新形式

3 光場(chǎng)位相算符的經(jīng)典對(duì)應(yīng)
作為(13)式的應(yīng)用,我們來(lái)推導(dǎo)位相算符的Weyl編序.利用

將其代入(13)式,得到

根據(jù)Weyl量子化理論[7],位相算符 e-iφ的Weyl對(duì)應(yīng)式為

由于Wigner算符Δ(α)的Weyl編序?yàn)閇13]

所以對(duì)照(15)式可見

這說(shuō)明位相算符的經(jīng)典對(duì)應(yīng)是

可見位相算符 e-iφ對(duì)應(yīng)的經(jīng)典位相體現(xiàn)在 eiφ,
同樣我們也可以算出 eiφ的Weyl編序式

所以算符 eiφ的經(jīng)典對(duì)應(yīng)為

4 產(chǎn)生算符和湮滅算符的逆的Weyl編序式及應(yīng)用
Dirac[14]首先考慮了湮滅算符的逆a-1.既然產(chǎn)生算符描述光子產(chǎn)生過(guò)程,產(chǎn)生算符的逆應(yīng)該描寫光子湮滅過(guò)程;反之,湮滅算符的逆應(yīng)該描寫產(chǎn)生過(guò)程.但要注意由于a|0〉=0,盡管aa-1=1,但a-1a/=1.用相干態(tài)和圍道積分的方法[15]可以將粒子數(shù)態(tài)|n〉表示為

這里的圍道C包括了z=0點(diǎn),在圍道積分下a-1e z a?|0〉=z-1ez a?|0〉就有了意義,于是有

即

a-1滿足

利用(24)式得到

將

代入(13)式得到

另一方面,直接利用(7)式又有

該式代入時(shí)利用了 a-1|β〉=β-1|β〉,比較 (28)和(29)兩式得到

由于Weyl編序中,產(chǎn)生算符與湮滅算符是可交換的,可以將其看作積分參量,從(30)式得到一個(gè)新的積分公式
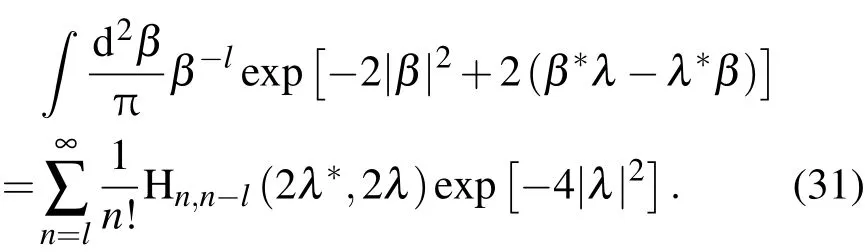
注意β-l是負(fù)冪次,所以這個(gè)積分帶有瑕點(diǎn),不易用常規(guī)的方法積分,這里用Weyl編序方法繞過(guò)了這一困難.()
同樣我們可以推導(dǎo)出a?-l的Weyl編序

由此可以悟出帶負(fù)冪次(β?)-l的新高斯積分公式

進(jìn)一步由(24)式可見

將

代入(13)式得

另一方面,直接利用(7)式又得到

比較以上兩式,可以悟出關(guān)于帶負(fù)冪次(β?)-kβ-l的新高∫斯 積分公式

進(jìn)一步可改寫為

作為比較,我們推導(dǎo)帶正冪次(β?)kβl的新高斯積分公式.將


另一方面,將(a?)kal直接代入(7)式得

比較以上兩式,可以悟出關(guān)于帶正冪次(β?)kβl的新積分公式

另一方面利用(10)式得到

比較(44)與(45)式,得出關(guān)于雙變量厄米特多項(xiàng)式的一個(gè)新的母函數(shù)公式
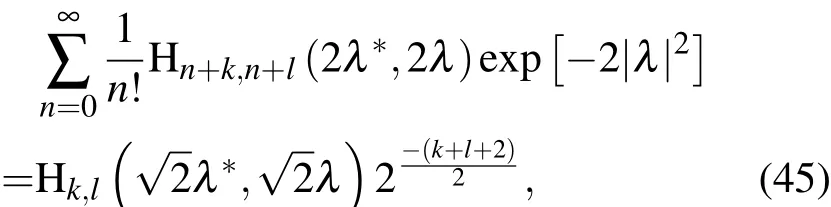
該式也可利用其他方法驗(yàn)證.
(45)式進(jìn)一步可改寫為

該式正好與(41)式相匹配.
5 結(jié)論
本文推導(dǎo)出了光場(chǎng)位相算符的Weyl編序,寫出了其經(jīng)典對(duì)應(yīng),這對(duì)于深入了解光場(chǎng)算符的性質(zhì)提供了一種新的途徑;推導(dǎo)了產(chǎn)生算符與湮滅算符的逆的Weyl編序,并據(jù)此推導(dǎo)出了某些特殊函數(shù)的新的生成函數(shù)和帶負(fù)次冪的高斯積分公式.
[1]Dirac PA M 1927 Proc.R.Soc.London A 114 243
[2]Carruthers P,Nieto M M 1968 Rev.Mod.Phys.40 411
[3]Wigner EP1932 Phys.Rev.40 749
[4]Klauder JR,Skagerstam B S1985 Coherent States(Singerpore:World Scientifi c Publishing)
[5]Scully M O,Zubairy M S 1997 Quantum Optics(United Kingdom:Cambridge University Press)
[6]Glauber RJ1963 Phys.Rev.130 2529
[7]Weyl H 1927 Z.Phys.A 46 1
[8]Fan HY 1992 J.Phys.A 25 3443
[9]Fan H Y,Hu L Y 2008 Chin.Phys.B 17 1640
[10]Yuan H C,Xu X X 2010 Acta Phys.Sin.61 064205(in Chinese)[袁洪春,徐學(xué)翔2012物理學(xué)報(bào)61 064205]
[11]Fan H Y 2008 Ann.Phys.323 1502
[12]Jiang N Q,Fan H Y,Hu L Y 2011 J.Phys.A:Math.Theor.44 195302
[13]Xu X X,Yuan H C,Hu L Y 2010 Acta Phys.Sin.59 4661(in Chinese)[徐學(xué)翔,袁洪春,胡利云2010物理學(xué)報(bào)59 4661]
[14]Dirac P A M 1966 Lectures on Quantum Field Theory(New York:Academic)
[15]Fan H Y 1993 Phys.Rev.A 47 4521

