YANG Bing-ka (楊冰卡), ZHU Ke-qiang (朱克強(qiáng)), ZHU Yan-jie (朱艷杰), QIN Dao-wu (秦道武) Maritime College, Ningbo University, Ningbo 315211, China, E-mail: bakerbing@gmail.com

Dynamic response of towed line array*

YANG Bing-ka (楊冰卡), ZHU Ke-qiang (朱克強(qiáng)), ZHU Yan-jie (朱艷杰), QIN Dao-wu (秦道武) Maritime College, Ningbo University, Ningbo 315211, China, E-mail: bakerbing@gmail.com

(Received January 8, 2013, Revised April 28, 2013)

Three-dimensional motion equations with consideration of the bending and torsional effects of a marine towed cable system under large elastic deformation conditions are formulated using the lumped parameter model. The lumped mass model is used to simulate a circular maneuver of a towed horizontal array that was first presented by Ablow. The results of this paper are in a good agreement with those obtained by finite difference schemes, and the minimum depth is closer to the experimental result. Although the calculations take more computation time, the lumped mass model is a good method, which can also be used to solve problems of towed line array, especially multi-branched towed line array, because of its flexibility.

towed cables, lumped mass, dynamic response

Introduction

Towed line arrays are an important tool that is towed behind ships or submarines for long-range target detection. Accurate location of the target requires accurate knowledge of the location of receiver. So the location of target can be estimated from a model that can accurately simulate the motion of the cable under known ship maneuvers.

The finite difference schemes are popular for solving ocean towing problems after Ablow and Schechter presented a finite difference model for the three-dimensional motion of a towed cable. Other similar analyses can be found in the papers by Howell and Koh. Recently, Gobat et al.[1-3]used the generalized αtime integration algorithm, the adaptive time stepping and the spatial gridding to extend the use of the classical finite difference schemes. The resulted algorithm can produce accurate and stable solutions for dynamic problems. There are parallel studies in China[4,5].

The finite elements and the lumped parameters can solve undersea cable problems. But the FE model applied to large displacement cable problems involves too much unnecessary operations, on the other hand, the lumped parameter model is very simple, which is in general applied in a wide range of offshore-related cable and pipeline problems with only three degrees of translational freedom for each computational node. So the latter is widely used in the analyses of cablelike structures[6-10].

This paper uses the lumped parameter model to simulate a circular maneuver of a towed horizontal array, and compares the results with the results obtained by finite difference schemes and experimental measurements. This investigation shows that the lumped parameter model is effective to simulate the motion of a towed line array.

1. Mathematical formulation

Consider a short element of the cable subjected to hydrodynamic load, gravity and internal load. The governing equations neglecting the shear deformation and the rotary inertia effects of motion for the cable can be written as:where sεthe stretched length, eT the effective tension vector, N the shear force vector,εG the distributed force per unit stretched length of cable, mεthe mass of cable per unit stretched length, M the internal moment vector, q the distributed moment load per unit stretched length of cable (generally, zero).

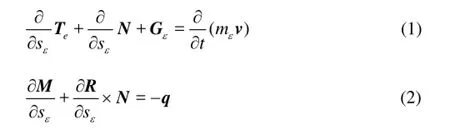
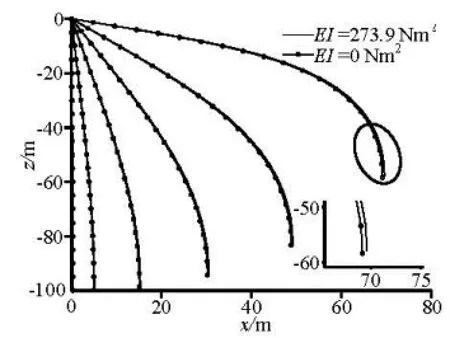
Fig.1 Comparison of the results with and without bending stiffness

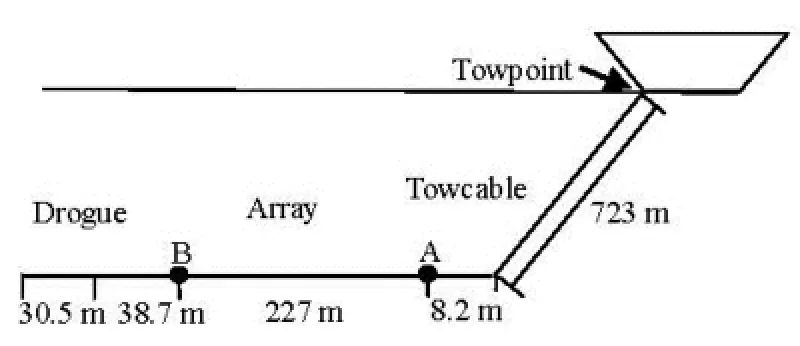
Fig.2 Towed array system

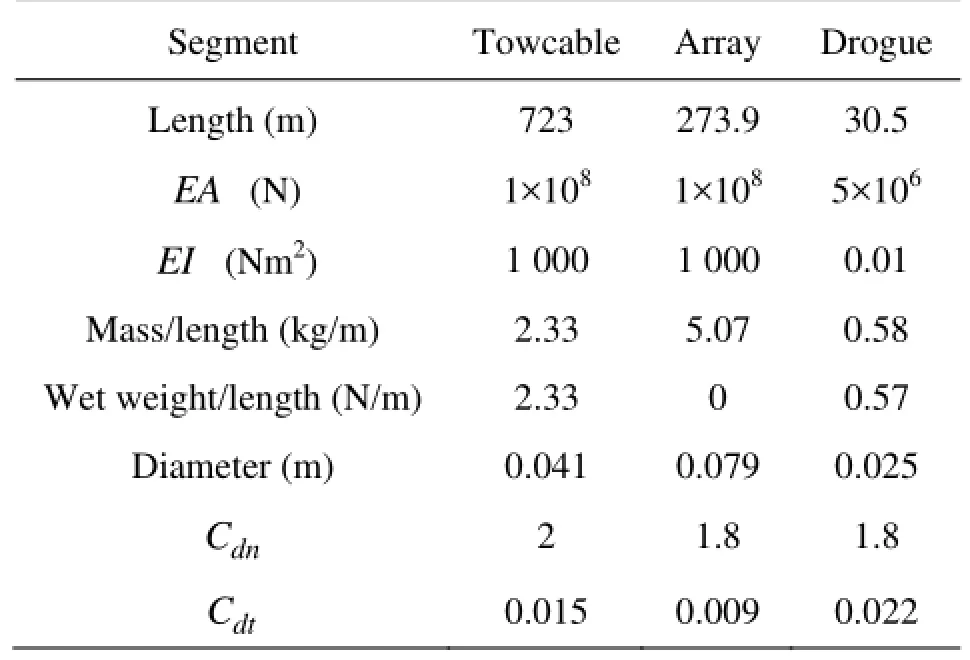
Table 1 Physical properties of the towed cable system

The basic idea is to discretize the line segment into a number of small finite elements with the mass of each element being concentrated into a node. The tension, the shear force and any external hydrodynamic load become the concentrated load acting on the node. All the lumped nodes are then connected together by linear or non-linear springs[11-13]. By replacing all the space derivative terms in the continuum equations with the finite difference approximations, the Lump Parameter equation of motion of the thi node (i=1,N+1) can be expressed as

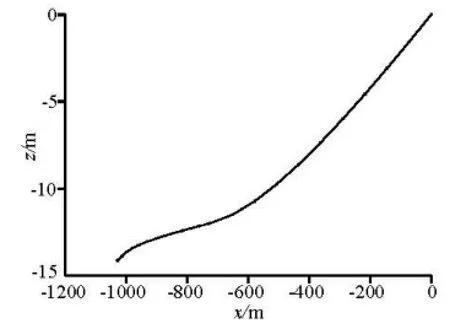
Fig.3 Steady state solution at 9.52 m/s

Fig.4 Plan view of circular manoeuvre

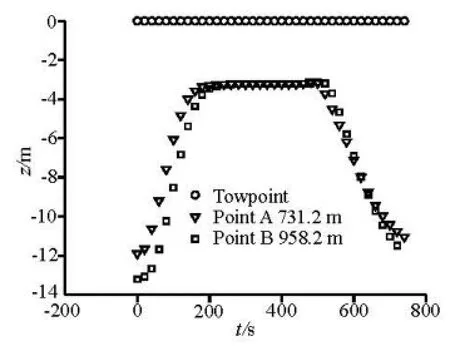
Fig.5 Depths in the loop turn of towpoint, Point A and Point B

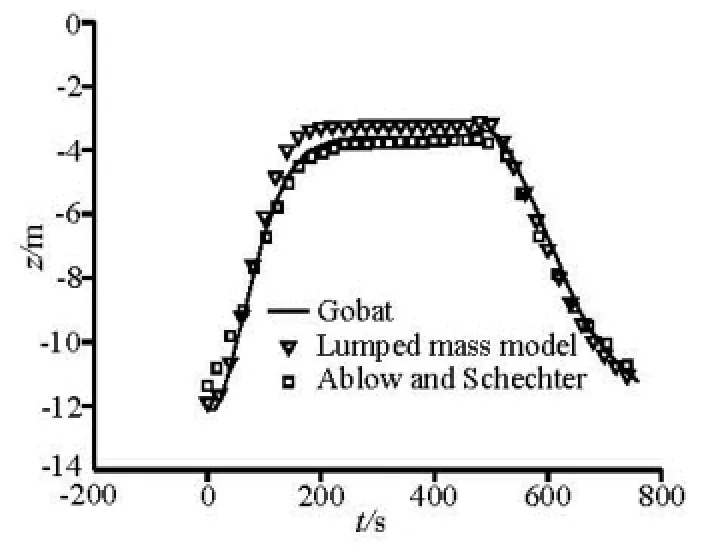
Fig.6 Variations of depth of Point A from Gobat, Ablow and this paper

where AiM the nodal mass matrix, iR the nodal position vector of cable, Tei=T+P0A the nodal effective tension vector,iw the weight of node in water per unit length,isεΔ the stretched length of segment,

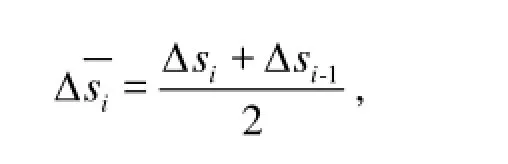
Δsithe original length of segment, Fithe nodal external fluid loading vector, Hithe nodal torsional moment vector, EI the bending stiffness.

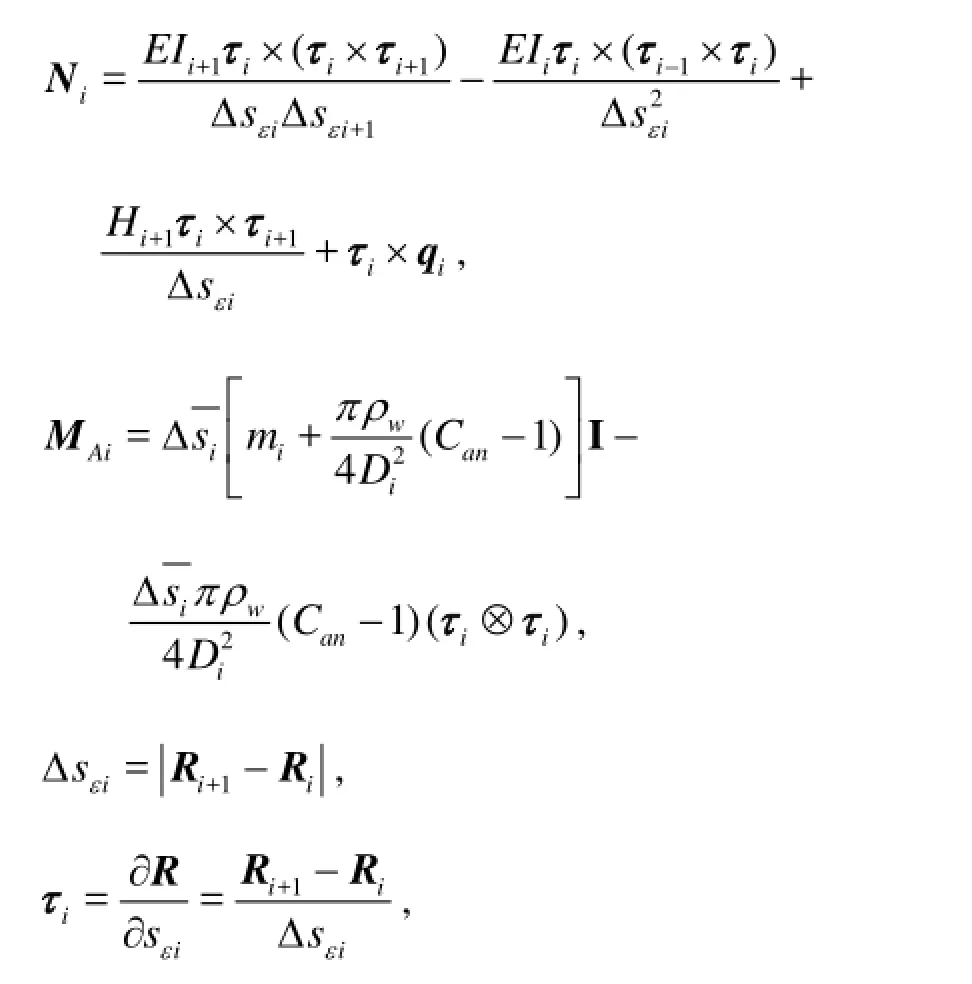
In order to evaluate the motion of the towed cable, the boundary conditions and the numerical integration schemes should be specified, as can be found in the papers[14,15].

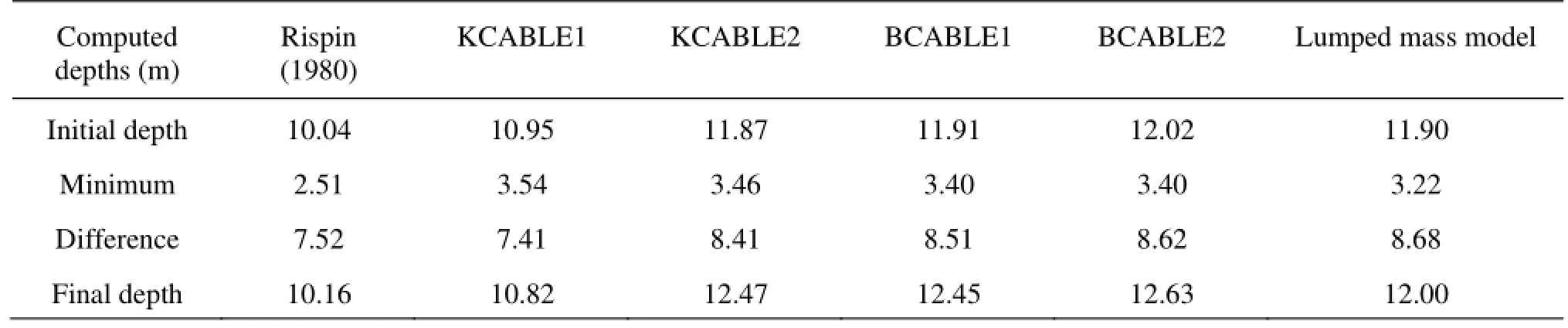
Table 2 Comparison of measured and computed results

2. Numerical applications

The bending moment effect is considered in this model. In order to see the effect, this model is used to simulate the falling of a 100 m neutrally buoyant cable with and without bending stiffness. The initial state of the cable is in the horizontal position. There is a weight of 98 N in one end of the cable. The diameter of the cable is 0.041 m. The axial stiffness of the cable, EA=4.4×106N. The bending stiffness, EI= 273.9 Nm2. The mass, =m0.992 kg/m. According to Fig.1, the effect of the bending stiffness is so small that two curves almost coincide.

Next, the model is used to simulate a circular maneuver of a towed horizontal array that was first presented by Ablow and Schechter. Figure 2 illustrates the array and Table 1 summarizes the physical properties of each segment, which are the same as those given by Gobat[3].

The whole process is as follows. The towpoint goes out at a fix heading for one second at 9.52 m/s (18.5 knots), then enters a loop of radius 0.64 km for 440 s, the ship comes out of the turn and continues moving in a tangential direction for 300 s.

Before this process, the towed array system is towed straightly in the vertical direction at the speed of 9.52 m/s to reach the steady state solution that is taken as the initial state of the loop turn. Figure 3 shows the solution.

Figures 4 and 5 show the movements of Point A and Point B. The variations of the depth of Point A are compared with the results of Gobat and Ablow (Fig.6). A comparison is also made among the experimental results of Rispin (1980), the results obtained by other finite difference schemes and the results of this paper (Table 2).

Figure 6 and Table 2 show that the results obtained based on the lumped mass model are consistent with the available results, and the minimum depth of Point A is closer to the measured depth. The total time of simulation is about 2 h, which is more than that spent on finite difference schemes. But the lumped approach can also be used to simulate the dynamic behavior of the multi-branched towed line array because of its flexibility.

3. Conclusion

A formulation based on the lumped mass model for solving three-dimensional problems of the towedline array is presented, the bending and torsional effects are taken into consideration. The 4th order Runge-Kutta integration is employed to solve the governing equations. Two cases are computed to validate the model. Although the time of simulation is more than that spent on finite difference schemes, the results are more accurate.

[1] GOBAT J. I., GROSENBAUGH M. A. Dynamics in the touch-down region of catenary moorings[J]. International Journal of Offshore and Polar Engineering, 2001,11(4): 273-281.

[2] GOBAT J. I., GROSENBAUGH M. A. and TRIANTAFYLLOU M. S. Generalized -α time integration solutions for hanging chain dynamics[J]. Journal of Engineering Mechanics, 2002, 128(6): 677-687.

[3] GOBAT J. I., GROSENBAUGH M. A. Time-domain numerical simulation of cable structures[J]. Ocean Engineering, 2006, 33(10): 1373-1400.

[4] ZHU Jun, PANG Yong-jie and XU Yu-ru. Numerical simulation of vibrating behaviors using towed cablearray[J]. The Ocean Enggineering, 2003, 21(2): 76-81(in Chinese).

[5] LIU Tao, ZHANG Wei-jing and MA Jie et al. Transient dynamic analysis of towed low-tension cable with experimental verification[J]. Journal of Ship Mechanics, 2013, 17(3): 197-213.

[6] ZHU Ke-qiang, ZHEN Dao-chang and ZHOU Jianghua et al. Station-keeping dynamic response of a moored production barge with multi-point mooring system[J]. Navigation of China, 2007, (2): 6-9(in Chinese).

[7] CHAI Y. T., VARYANI K. S. and BARLTROP N. D. P. Three-dimensional lump-mass formulation of a catenart riser with bending, torsion and irregular seabed interaction effect[J]. Ocean Engineering, 2002, 29(12): 1503-1525.

[8] ZHU Ke-qiang, ZHENG Dao-chang and CAI Ying et al. Nonline hydrodynamic rssponse of marine cablesystem undergoing random dynamic excitation[J]. Journal of Hydrodynamics, 2009, 21(6): 851-855.

[9] WANG fei, HUANG Guo-liang and DENG De-heng. Dynamic response analysis of towed cable during deployment/retrieval[J]. Journal of Shangihai Jiaotong University (Science), 2008, 13(2): 245-251.

[10] WANG Fei, MA Jian-wen and HUANG Guo-liang. Dynamic modeling and analysis of towed low tension cable with bending and torsion effect[J]. Journal of Shanghai Jiaotong University, 2012, 46(3): 451-457(in Chinese).

[11] ZHU Ke-qiang, ZHENG Dao-chang and ZHOU Jianghua et al. Dynamic analysis on ocean cables system with lumped parameter approach[J]. Navigation of China, 2007, (3): 10-12(in Chinese).

[12] ZHAO Yun-peng, LI Yu-cheng and GUI Fu-kun et al. Numerical simulation of the effects of weight system on the hydrodynamic behavior of 3-D net of gravity cage in current[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(4): 442-452.

[13] ZHU Ke-qiang. LI Dao-geng and LI Wei-yang. Lumped-parameter analysis method for time-domain of ocean cable-body systems[J]. The Ocean Engineering, 2002, 20(2): 100-102(in Chinese).

[14] ZHU Ke-qiang, ZHU Hai-yang and YU Chun-ling et al. A simulation of nonlinear coupling dynamic characteristic on a deep-sea tethered remotely operated vehicle multi-body system[J]. The Ocean Engineering, 2008, 26(1): 83-87(in Chinese).

[15] ZHU Ke-qiang, ZHU Hai-yang and ZHANG Yu-song et al. A multi-body space coupled motion simulation of hydrodynamics on a deep-sea tethered remotrly operated vehicle[J]. Journal of Hydrodynamics, 2008, 20(2): 210-215.

10.1016/S1001-6058(11)60403-5

* Project supported by the Science Program of Ningbo City (Grant No. szxl1066) the Program for Changjiang Scholars and Innovative Research Programs in Higher Learning Institutions (Grant No. IRT0734) and the National Natural Science Foundation of China (Grant Nos. 11272060 and 10872098).

Biography: YANG Bing-ka (1987-), Male, Ph. D. Candidate

ZHU Ke-qiang, E-mail: zhukeqiang@nbu.edu.cn