Ground states for asymptotically periodic quasilinearSchr?dinger equations with critical growth
Zhang Hui Zhang Fubao
(Department of Mathematics, Southeast University, Nanjing 211189, China)
1 Introduction and Statement of Main Result
As the models of physical phenomena, the quasilinear Schr?dinger equation
(1)
has been extensively studied in recent years. For the detailed physical applications, one can see Ref.[1].
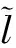
Inspired by Refs.[4-5], we are interested in the existence of ground states for asymptotically periodic quasilinear Schr?dinger equation (1). We consider
-Δu+V(x)u-uΔ(u2)=K(x)|u|22*-2u+g(x,u)
u∈H1(RN)
(2)
LetFbe a class of functionsh∈C(RN)∩L∞(RN), such that for every>0 the set {x∈RN:|h(x)|≥} has a finite Lebesgue measure. Suppose thatV,K∈C(RN) satisfies the following conditions:
H1) There exists a constanta0>0 and a functionVp∈C(RN), 1-periodic inxi, 1≤i≤N, such thatV-Vp∈FandVp(x)≥V(x)≥a0,x∈RN.
H2) There exists a functionKp∈C(RN), 1-periodic inxi, 1≤i≤N, and a pointx0∈RNsuch thatK-Kp∈Fand
①K(x)≥Kp(x)>0,x∈RN;
②K(x)=|K|∞+O(|x-x0|N-2), asx→x0.
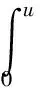
H3)g(x,u)=o(u) uniformly inxasu→0;
H4) |g(x,u)|≤a(1+|u|q-1), for somea>0 and 4≤q<22*;
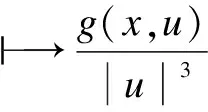
H6) There exists a neighborhood ofx0given by H2),Ω?RN, such that
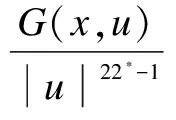
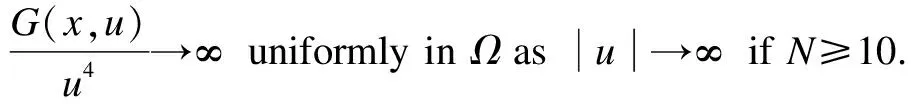
H7) There exists a constantq1∈(2,22*), functionsh∈Fandgp∈C(RN×R,R) such that
①gpis 1-periodic inxi,1≤i≤N;
② |g(x,u)-gp(x,u)|≤|h(x)|(|u|+|u|q1-1),x∈RN;
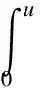

Theorem1If H1) to H7) hold, then the problem (2) has a ground state.
Remark1H3) and H5) imply that
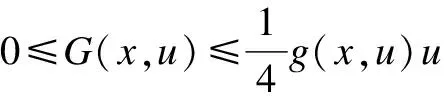
(3)
2 Variational Setting
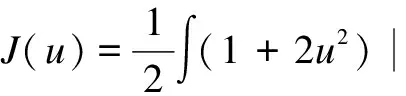
is not well defined inH1(RN). Choose the changefdefined by
f(t)=-f(-t) on (-∞,0]
and setv=f-1(u), then we obtain
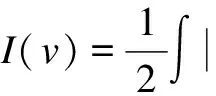
which is well defined inH1(RN) by the properties off(see Ref.[5]). The critical points ofIare weak solutions of
-Δv+V(x)f′(v)f(v)=K(x)|f(v)|22*-2f(v)f′(v)+g(x,f(v))f′(v)v∈H1(RN)
(4)
Similar to Ref.[5], we first prove that there is a nontrivial solution for Eq.(4). We know that the results obtained under (V), (K), (g1), (g2) and (g5) in Ref.[5] still hold since the conditions H1) to H4) and H6) are the same as (V), (K), (g1), (g2) and (g5), respectively. However, H5) and H7) are different from (g3) and (g4) in Ref.[5]; in the following, we verify whether the results under (g3) and (g4) still hold.
Lemma1Let H1) to H5) hold. Then, the (Ce)b(b>0) sequencevnofIsatisfying
I(vn)→b, =I′(vn)=(1+=vn=)→0
(5)
is bounded.
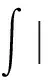
By (5), we have
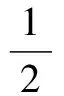

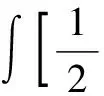
I1+I2+I3
(6)
By Lemma 1 (8) in Ref.[5], we obtain
(7)
ForI3, using Lemma 1 (8) in Ref.[5] and inequality (3), we have
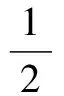
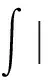
In Ref.[5], the authors supposed that |g(x,u)-gp(x,u)|≤h(x)|u|q3-1,q3∈[2,22*), and we assume that |g(x,u)-gp(x,u)|≤h(x)(|u|+|u|q1-1),q1∈(2,22*). So Lemma 9 in Ref.[5] holds under H1), H2) and H7). Following the outline in Ref.[5], we have the following lemma.
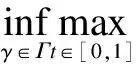
In order to find ground states, we also need to introduce the Nehari manifold. The Nehari manifold corresponding to Eq.(4) is
M={u∈H1(RN){0}: 〈I′(u),u〉=0}
First, we give the following lemma in which the simple proof is left to the reader.
Lemma3Let H1) to H5) hold. ThenI(tu)→-∞ ast→∞,u∈H1(RN){0}.
Inspired by Ref.[6], we have
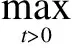
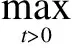
Note that

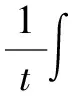
t(|v+Φ1(t)+Φ2(t)+Φ3(t))
By Lemma 1 (8) in Ref.[5] and the fact thatf″(tv)=-2f(tv)f′4(tv), we obtain
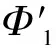

2f2(tv)f′4(tv)tv2-f(tv)f′(tv)v]V(x)<0
SoΦ1is decreasing.
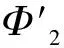
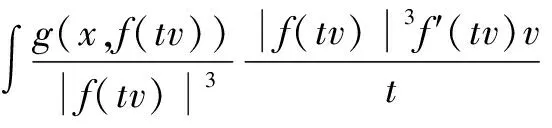
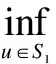
(8)
Lemma5Let H1) to H6) hold. Thenc*≥c.
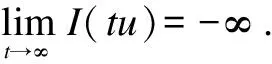
3 Proof of Theorem 1
ProofBy Lemma 2, we assume that there is a nontrivial solutionwwithI(w)=c. Thenw∈M. SoI(w)≥c*. Note thatI(w)=candc*≥c, and we obtainI(w)≤c*. SoI(w)=c*. Then we can easily infer thatwis a ground state for Eq.(4). We complete the proof.
[1]Kurihara S. Large-amplitude quasi-solitons in superfluid films [J].JournalofthePhysicalSocietyofJapan, 1981,50(10): 3262-3267.
[2]Liu J, Wang Z. Soliton solutions for quasilinear Schr?dinger equations Ⅰ [J].ProceedingsoftheAmericanMathematicalSociety, 2003,131(2): 441-448.
[3]Liu J, Wang Y, Wang Z. Solutions for quasilinear Schr?dinger equations via the Nehari method [J].CommunicationsinPartialDifferentialEquations, 2004,29(5/6): 879-901.
[4]Liu X, Liu J, Wang Z. Ground states for quasilinear Schr?dinger equation with critical growth [J].CalculusofVariationsandPartialDifferentialEquations, 2013,46(3/4): 641-669.
[5]Silva E A B, Vieira G F. Quasilinear asymptotically periodic elliptic equations with critical growth [J].CalculusofVariationsandPartialDifferentialEquations, 2012,39(1/2): 1-33.
[6]Szulkin A, Weth T. The method of Nehari manifold [C]//HandbookofNonconvexAnalysisandApplications. Boston, USA: International Press, 2010: 597-632.
[7]Do J M, Miyagaki O H, Soares S H M. Soliton solutions for quasilinear Schr?dinger equations with critical growth [J].JournalofDifferentialEquations, 2010,248(4): 722-744.
[8]Silva E A B, Vieira G F. Quasilinear asymptotically periodic Schr?dinger equations with subcritical growth [J].NonlinearAnalysis:Theory,MethodsandApplications, 2010,72(6): 2935-2949.
 Journal of Southeast University(English Edition)2013年3期
Journal of Southeast University(English Edition)2013年3期
- Journal of Southeast University(English Edition)的其它文章
- Method of variation of parametersfor solving a constrained Birkhoffian system
- Optimal dispatching method of traffic incident rescue resource for freeway network
- Approach to estimationof vehicle-road longitudinal friction coefficient
- Smoke distribution in naturally ventilated urban transportation tunnels with multiple shafts
- Towing characteristics of large-scale composite bucket foundation for offshore wind turbines
- Development of overlay tester for fracture test of asphalt mixture
