Wang Xiaoliu Chao Xiaoli

(Department of Mathematics, Southeast University, Nanjing 211189, China)

Since the 19th century, the ruled surfaces have captured the attention of mathematicians and the main properties of these surfaces have been illuminated in almost all the monographs and books on differential geometry. Motivated again by their flatness property, in this paper we classify some ruled surfaces endowed with the constancy angle property. The constant angle surfaces was initially studied in the setting of the product spaceS2×R(see Ref.[1]). Then the surfaces with this property in other ambient spaces, namelyH2×RandR3, were investigated[2-4]. One may also find other relative references in Refs.[5-7].

1 Preliminaries

t′(s)=κ(s)n(s)

n′(s)=-κ(s)t(s)+τ(s)b(s)

(1)

b′(s)=-τ(s)n(s)

whereτ(s) is the torsion of curveσats.

2 Main Theorems and Their Proof

First, we consider ruled surfaceS

r(s,v)=σ(s)+vl(s)

(2)

where

l(s)=cosα(s)·t(s)+sinα(s)·n(s)

Set

m(s)=-sinα(s)·t(s)+cosα(s)·n(s)

It is easy to know thatm(s) is orthogonal to bothl(s) andb(s). Moreover, we have

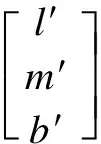
A direct computation shows that

rs=σ′(s)+vl′(s)=(1-vα′sinα-vκsinα)t+

v(κ+α′)cosα·n+vτsinα·b

rv=l(s)=cosα·t+sinα·n

The normal of the surface is

(3)

whereΔ=(sinα-v(α′+κ))2+v2τ2sin2α.

If surfaceSis a constant angle surface； i.e., the normalNmakes a constant angleθwith the fixed directionk, namely ∠(N,k)=θ; equivalently, 〈N,k〉=cosθ. Substituting (3) into this expression, we obtain a vanishing polynomial expression of the second order inv. So all the coefficients must be identically zero, that is

sin2α(〈b,k〉2-cos2θ)=0

(4)

sinα(α′+κ)(〈b,k〉2-cos2θ)-τsin2α〈b,k〉〈m,k〉=0

(5)

(α′+κ)2(〈b,k〉2-cos2θ)-2τ〈b,k〉sinα(α′+κ)〈m,k〉+

τ2sin2α〈m,k〉2-τ2sin2αcos2θ=0

(6)

If sinα≡0, thenSis a tangent developmental surface which is given by[8]

r(u,v)=(ucosθ(cosv,sinv)+γ(v),usinθ)

(7)

with

(8)

and

(9)

whereλis a nonzero constant.

If sinα≠0, from Eq.(4) we have

〈b,k〉=±cosθ

(10)

Then Eq.(5) results in

τ〈b,k〉 〈m,k〉=0

(11)

Whenτ≡0,σis a plane curve whose binormal coincides with the normal of the plane, soSis a ruled surface with plane curveσas the generating curve andl(s) as the rulings. Obviously,Sis a piece of a plane.

Whenτ≠0, we claim that 〈b,k〉〈m,k〉=0. Indeed, if 〈b,k〉=0 at somewhere ofS, from Eq.(10), we obtain that cosθ=0 at the same point. Then Eq.(6) results in

〈m,k〉=0

(12)

On the other hand, if 〈m,k〉=0 at somewhere ofS, then from Eq.(6) we obtain that cosθ=0 at the same point; i.e., 〈b,k〉=0. Thus, the claim is true. Now differentiating in 〈b,k〉=0 yields 〈n,k〉=0. Combining 〈m,k〉=0, we can obtain that 〈t,k〉=0. Now we deduce thatkis orthogonal to allt,nandb, which is impossible.

Thus we prove our first main theorem.

Theorem1Assume that the ruled surfaceS:r(s,v)=σ(s)+v(cosα(s)·t(s)+sinα(s)·n(s)) is a constant angle surface. ThenSis locally isometric to one of the following surfaces:

1) A surface is given by

r(u,v)=(ucosθ(cosv,sinv)+γ(v),usinθ)

2) A piece of a plane.

Remark1We have known that the tangent developmental constant angle surfaces are generated by cylindrical helices and the normal constant angle surfaces are generated by planar curves (see Theorem 1 and Theorem 5 in Ref.[8]). From the proof of Theorem 1, the generating curves of the constant angle surfacesr(s,v)=σ(s)+v(cosα(s)·t(s)+sinα(s)·n(s)) are also planar curves provided sinα(s)≠0.

In the sequel we consider another kind of ruled surfaceS, which is defined by

r(s,v)=σ(s)+vl(s)

(13)

where

l(s)=cosα(s)·n(s)+sinα(s)·b(s)

Set

m(s)=-sinα(s)·n(s)+cosα(s)·b(s)

It is easy to know thatm(s) is orthogonal to bothl(s) andt(s). We have

Now we compute the normal toS. A routine computation shows

rs=σ′(s)+vl′(s)=(1-κvcosα)t-vsinα(τ+α′)n+

vcosα(τ+α′)b

rv=l(s)=cosα·n+sinα·b

Then the normal of the surface is

(14)

whereΔ=(1-κvcosα)2+v2(τ+α′)2.

Assume that surfaceSis a constant angle surface. Then there is a fixed directionkand a constant angleθsuch that 〈N,k〉=cosθ. Substituting Eq.(14) into this expression and comparing the coefficients in the vanishing polynomial expression of the second order inv, we find the following relationships:

〈m,k〉2=cos2θ

(15)

κsinα(〈m,k〉2-cos2θ)+(τ+α′)〈t,k〉〈m,k〉=0

(16)

κ2cos2α(〈m,k〉2-cos2θ)+(τ+α′)2(〈t,k〉2-cos2θ)+

2κcosα〈m,k〉〈t,k〉(τ+α′)=0

(17)

We claim thatτ+α′≡0. Suppose thatτ+α′≠0. A contradiction will be deduced. From Eq.(15), we have

〈m,k〉=±cosθ

(18)

From Eqs.(16) and (17), we obtain

(τ+α′)2(〈t,k〉2-cos2θ)=0

and thus〈t,k〉2=cos2θ=〈m,k〉2.

At the same time, Eq.(16) shows that 〈t,k〉 〈m,k〉=0, which implies that 〈t,k〉=〈m,k〉=0. Taking the derivative in Eq.(18) and using 〈t,k〉=0, we obtain that 〈l,k〉=0. This is impossible sincekcannot be orthogonal to allt,l,m. Thus, we prove thatτ+α′≡0.

Our aim is to showSis locally isometric to a plane or a cylinder. Ifκ≡0 locally, thenτ≡0 and α is a constant, which means thatSis locally a piece of a plane. So we only need to consider the case ofκ≠0. Taking the derivative into Eq.(18), we have

κ〈t,k〉sinα=(α′+τ) 〈l,k〉=0

When sin≡0,l≡nandSis a piece of a plane by Ref.[8]. When sinα≠0, 〈t,k〉=0 locally. We have the following computations:

〈t,k〉 =0?〈t′,k〉=0?κ〈l,k〉cosα=κ〈m,k〉 sinα?

κ〈cosα·n+sinα·b,k〉cosα=

κ〈-sinα·n+cosα·b,k〉sinα?

〈n,k〉=0?〈n′,k〉=0?τ〈b,k〉=0

where 〈b,k〉 cannot be zero sincekcannot be orthogonal to allt,n,b. Thenτ≡0 locally. Recall thatτ+α′≡0. We know thatαis a constant andSis locally a cylindrical surface.

In the end, our second main theorem reads as follows.

Theorem2Assume that the ruled surfaceS:r(s,v)=σ(s)+v(cosα(s)·n(s)+sinα(s)·b(s)) is a constant angle surface. ThenSis locally isometric to a plane or a cylindrical surface.

[1]Dillen F, Fastenakels J, van der Veken J, et al. Constant angle surfaces inS2×R[J].MonatsheftefürMathematik, 2007,152(2): 89-96.

[2]Dillen F, Munteanu M I. Surfaces inH+×R[C]//ProceedingsoftheConferencePureandAppliedDifferentialGeometry. Brussels, Belgium, 2007: 185-193.

[3]Dillen F, Munteanu M I. Constant angle surfaces inH2×R[J].BullBrazMathSoc, 2009,40(1): 85-97.

[4]Munteanu M I, Nistor A I. A new approach on constant angle surfaces inE3[J].TurkishJMath, 2009,33(2): 169-178.

[5]López R, Munteanu M I. Constant angle surfaces in Minkowski space [J].BullBelgMathSocSimonStevin, 2011,18(2): 271-286.

[6]Munteanu M I. From golden spirals to constant slope surfaces [J].JournalofMathematicalPhysics, 2010,51(7): 073507.

[7]Di Scala A J, Ruiz-Hernández G. Helix submanifolds of euclidean spaces [J].MonatsheftefürMathematik, 2009,157(3): 205-215.

[8]Nistor A I. Certain constant angle surfaces constructed on curves [J].IntElectronJGeom, 2011,4(1): 79-87.