Construction of semisimple categoryover generalized Yetter-Drinfeld modules
Zhang Xiaohui Wang Shuanhong
(Department of Mathematics, Southeast University, Nanjing 211189, China)
In 2007, Panaite and Staic[1]introduced the notion of generalized Yetter-Drinfeld modules which covered both Yetter-Drinfeld modules and anti-Yetter-Drinfeld modules. Liu and Wang[2]studied the notion of generalized weak Yetter-Drinfeld modules and made the category ofHWYDH(α,β) into a braided T-category[3]. The fusion category[4-6]plays an important role in classifying the semisimple Hopf algebra. The semisimple category is the first step to construct a fusion category. In this paper, we discuss the following question: how to make the category of generalized Yetter-Drinfeld modulesHYDH(α,β) into a semisimple category.
Throughout this paper, we assume thatHis a Hopf algebra[7-8]with a bijective antipode over a fieldk. Denote the set of all the automorphisms ofHby AutHopf(H). Letα,β∈AutHopf(H).
1 Preliminaries
Definition1For anyα,β∈AutHopf(H), a (α,β)-Yetter-Drinfeld module is ak-moduleM, such thatMis a leftH-module (with notationh?m|→h·m) and a rightH-comodule (with notationm|→m(0)?m(1)) with the following compatibility condition:
ρ(h·m)=h2·m(0)?β(h3)m(1)α(S-1(h1))
for allh∈Handm∈M. The category of (α,β)-Yetter-Drinfeld modules andH-linearH-colinear maps is denoted byHYDH(α,β).
Define the category of the generalized Yetter-Drinfeld module YD(H) as the disjoint union of allHYDH(α,β).
Definition2Suppose thatM∈YD(H), thenMis called simple if it has no proper subobjects. A direct sum of simple objects is called semisimple. If every objectM∈YD(H) is semisimple, we call the category YD(H) semisimple.
2 Making YD(H) into semisimple
Lemma1[1]Suppose thatM∈HYDH(α,β) andN∈HYDH(γ,δ), thenM?N∈HYDH(αγ,δγ-1βγ) with the following structures
h·(m?n)=γ(h1)·m?γ-1βγ(h2)·n
m?n|→(m?n)(0)?(m?n)(1)=(m(0)?n(0))?n(1)m(1)
Lemma2Ifkis a commutative ring,His a commutative Hopf algebra overk,M∈HYDH(α,β),N∈HYDH(γ,δ), andMis a finitely generated projectiveH-module, then
1)Hhom(M,N) is anH-comodule, andHhomH(M,N)=Hhom(M,N)coH, where theH-coaction is given byρ(f)(m)=f0(m)?f1f(m0)0?f(m0)1S(m1).
2)Hhom(M,N)∈HYDH(α,β), where theH-action is given by (h·f)(m)hf(m)=f(h·m).
Proof1) Define a mapπ:Hhom(M,N)→Hhom(M,N?H) byπ(f)(m)=f(m0)0?f(m0)1S(m1).
For anym∈M,h∈H, we have
π(f)(h·m)=f((h·m)0)0?f((h·m)0)1S((h·m)1)=
f(h2·m0)0?f(h2·m0)1S(β(h3)m1α(S-1(h1)))=
h·f(m0)0?β(h3)β(S(h4))f(m0)1α(S-1(h2))·
α(h1)S(m1)=h·f(m0)0?f(m0)1S(m1)=
h·(π(f))(m))
Thus,πis well defined. SinceMis a finitely generated projectiveH-module, we haveHhom(M,N?H)?Hhom(M,N)?H. So we obtain a map:
ρ:Hhom(M,N)→Hhom(M,N)?H
such thatρ(f)(m)=f(m0)0?f(m0)1S(m1), andHhom(M,N)∈MH.
Now for anyf∈Hhom(M,N), iffisH-colinear, then
ρ(f)(m)=f(m0)0?f(m0)1S(m1)=
f(m0)?m1S(m2)=f(m)?1=(f?1)(m)
Sofis coinvariant. Conversely, takef∈Hhom(M,N)coH, then we have
ρN(f(m))=f(m0)0?f(m0)1ε(m1)=
f(m0)0?f(m0)1S(m1)m2=f(m0)?m1
for anym∈M, andfisH-linear. Thus,HhomH(M,N)=Hhom(M,N)coH.
2) For anym∈M,h∈H, we have
((h·f)0?(h·f)1)(m)=(h·f(m0))0?
(h·f(m0))1S(m1)=h2·f(m0)0?
β(h3)f(m0)1α(S-1(h1))S(m1)=
(h2·f0?β(h3)f1α(S-1(h1)))(m)
Lemma3LetVbe ak-module andNbe anH-module, then
1)Hhom(H?V,N) and hom(V,N) are isomorphic ask-modules, where the bijection is given byθ:Hhom(H?V,N)→hom(V,N),θ(f)(v)=f(1?v).
2) IfVis a projectivek-module, thenH?Vis a projectiveH-module.
Furthermore, ifV∈MH, thenH?Vis an object ofHYDH(α,β) via
h·(h′?v)=hh′?v
ρ(h?v)=h2?v0?β(h3)v1α(S-1(h1))
Similar to Lemma 2, we can obtain the following lemmas.
Lemma4LetV∈MHis a finitely generated projectivek-module. Then for anyH-comoduleN, we have hom(V,N)∈MH, where theH-coaction is given byρ(g)(v)=g(v0)0?g(v0)1S(v1). IfHis commutative, then for anyN∈HYDH(α,β), we can getHhom(H?V,N)∈HYDH(α,β).
Lemma5Suppose thatHis commutative, andN∈HYDH(α,β).
1) IfV∈MHis a finitely generated projectivek-module, thenHhom(H?V,N) and hom(V,N) are isomorphic asH-comodules.
2) Ifkis a field,Vis a finite-dimensionalk-space and a projective rightH-comodule, thenH?Vis a projective object inHYDH(α,β).
Proof1) It is straightforward.
2) Obviously, we have
HhomH(H?V,N)?Hhom(H?V,N)coH?
hom(V,N)coH?homH(V,N)
where the last isomorphism is due to the proof of Lemma 2. So the conclusion holds. From the above two lemmas, we have the following facts.
Lemma6Letkbe a field, andM∈HYDH(α,β). ThenMis a finitely generatedH-module if and only if there exists a finite dimensionalH-comoduleVand anH-linearH-colinear epimorphismπ:H?V→M.
LetH*be the linear dual ofH. IfM,N∈MH, then homk(M,N)∈H*Munder the followingH*-action
(h*·f)(m)=h*(f(m0)1S(m1))·f(m0)0
Lemma7Assume thatHis commutative, andM,N∈HYDH(α,β). ThenHhom(M,N) is a leftH*-submodule of homk(M,N).
Furthermore,M∈H*Mis called rational if the leftH*-action onMis induced by a rightH-coaction onM.
Proposition1Suppose thatHis commutative,kis a field,M,N∈HYDH(α,β), andMis a finitely generatedH-module. ThenHhom(M,N)∈HYDH(α,β).
ProofBy Lemma 6, there exists a finite dimensionalH-comoduleVand anH-linearH-colinear epimorphismπ:H?V→M. So we obtain an injectivek-linear mapHhom(π,N):Hhom(M,N)→Hhom(H?V,N). For anyφ∈H*,v∈V,h∈H,f∈Hhom(M,N), we haveπ(h?v)=h·v,ρ(1?v)=1?v0?v1, and
((φ·f)°π)(1?v)=(φ·f)(v)=
φ(f(v0)1S(v1))f(v0)0=
φ(f(π(1?v0))1S(v1))f(π(1?v0))0=
φ(f(π(1?v)0)1S(1?v)1)f(π(1?v)0)0=
(φ·(f°π))(1?v)
It follows thatHhom(π,N) isH*-linear. Then by Lemma 2,Hhom(H?V,N) is anH-comodule, and, therefore, a rationalH*-module. ThusHhom(M,N) is a rationalH*-submodule ofHhom(H?V,N). This means thatHhom(M,N) is anH-comodule. Then we obtainHhom(M,N)∈HYDH(α,β) by Lemma 2.
We say thatHYDH(α,β) satisfies the exact condition if the following property holds: ifM∈HYDH(α,β) is a finitely generatedH-module, then the functorHhom(M,_):HYDH(α,β)→HYDH(α,β) is exact.
By Proposition 1, ifHis commutative andMis a finitely generatedH-module, we haveHhom(M,N)∈HYDH(α,β) for anyN∈HYDH(α,β). ObviouslyHYDH(α,β) satisfies the exact condition ifHis semisimple.
Proposition2Assume thatHis commutative, andHYDH(α,β) satisfies the exact condition and the functor (-)coH:HYDH(α,β)→kMis exact. Then any finitely generatedH-moduleM∈HYDH(α,β) is a projective object.
Proofwe haveHhomH(M,_)?Hhom(M,_)coH=(-)coH°Hhom(M,_) which implies thatHhomH(M,_) is also an exact functor.
Proposition3Under the same condition of Proposition 2, suppose thatHis noetherian. Then any finitely generatedH-moduleM∈HYDH(α,β) is a direct sum of a family of simple subobjects which are also finitely generated asH-modules inHYDH(α,β).
ProofAssume thatNis a subobject ofM. ThenNandM/Nare finitely generatedH-modules sinceHis noetherian. Furthermore,NandM/Nare projective objects. So we have a split exact sequence inHYDH(α,β): 0→N→M→M/N→0.
Thus the conclusion holds.
TakeM∈HYDH(α,β) and anH-subcomoduleVofM. We set
whereIis a finite set. ThenHVis a subobject ofMinHYDH(α,β) via:
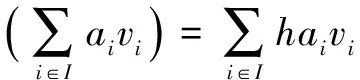
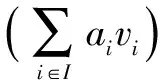
Theorem1LetHbe commutative and noetherian,HYDH(α,β) satisfies the exact condition and the functor (-)coH:HYDH(α,β)→kMis exact. Then everyM∈HYDH(α,β) is a direct sum of a family of simple subobjects ofMwhich are finitely generated asH-modules inHYDH(α,β). Therefore,HYDH(α,β) is a semisimple category.
ProofFor anym∈M,mbelongs to a finite dimensionalH-subcomoduleVmofM. ThenVmis a finitely generatedH-module. By Proposition 3,Vmis a direct sum of a family of simple subobjects which are finitely generated. LetΩbe the set of all direct sumsN=?i∈INiwhere everyNiis both a finitely generatedH-module and a simple subobject ofMinHYDH(α,β). Then the sum of two elements inΩis also an object inΩ. ThusΩcontains a maximal elementM′ through Zorn’s Lemma. For anym∈M, we havem∈HVm∈Ω. This means thatHVm+M′=M′. SoM=M′. Thus, the conclusion holds.
Corollary1LetHbe commutative and noetherian (particularly finite dimensional), semisimple and cosemisimple. Then eachM∈HYDH(α,β) is a direct sum of a family of simple subobjects ofMwhich are finitely generated asH-modules inHYDH(α,β). HenceHYDH(α,β) is a semisimple category.
ProofSinceHis cosemisimple, the functor (-)coH:MH→kMis exact. Thus (-)coH:HYDH(α,β)→kMis exact. Furthermore, the semisimplicity implies thatHYDH(α,β) satisfies the exact condition. Then by Theorem 1, the conclusion holds.
Theorem2As the disjoint union of allHYDH(α,β), the category of the generalized Yetter-Drinfeld modules YD(H) is also semisimple.
[1]Panaite F, Staic M D. Generalized (anti) Yetter-Drinfeld modules as components of a braided T-category [J].IsraelJMath, 2007,158(1): 349-365.
[2]Liu L, Wang S H. Constructing new braided T-categories over weak Hopf algebras [J].ApplCategorStruct, 2010,18(4): 431-459.
[3]Turaev V.Homotopyquantumfieldtheory[M]. Bloomington: European Mathematical Society, 2010.
[4]Etingof P, Nikshych D, Ostrik V. On fusion categories [J].AnnalsofMathematics, 2005,162(2): 581-642.
[5]Drinfeld V, Gelaki S, Nikshych D, Ostrik V. On braided fusion categories Ⅰ [J].SelectaMathematica, 2010,16(1): 1-119.
[6]Naidu D, Rowell E. A finiteness property for braided fusion categories [J].AlgebrRepresentTheor, 2011,14(5): 837-855.
[7]Sweedler M.Hopfalgebras[M]. New York: Benjamin, 1969.
[8]Montgomery S.Hopfalgebrasandtheiractionsonrings[M]. Rhode Island: American Mathematical Society, 1993.
 Journal of Southeast University(English Edition)2013年4期
Journal of Southeast University(English Edition)2013年4期
- Journal of Southeast University(English Edition)的其它文章
- Elastoplastic response of functionally graded cemented carbidesdue to thermal loading
- Effect of aggregation intervalon vehicular traffic flow heteroscedasticity
- Application of neural network merging model in dam deformation analysis
- Mechanical analysis of transmission lines based on linear sliding cable element
- Improvement of pump-probe optical measurement technique using double moving stages
- Improvement of pump-probe optical measurement technique using double moving stages
