Hu Changhui Lu Xiaobo Du Yijun Chen Wujun

(School of Automation, Southeast University, Nanjing 210096, China)(Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education, Southeast University, Nanjing 210096, China)

The direct linear discriminant analysis (DLDA) is an important method for dimension reduction and feature extraction in many applications such as face recognition[1-3], microarray data classification[4], text classification[5]. Yu and Yang[1]first proposed the DLDA algorithm based on eigenvalue decomposition (DLDA/EVD) by utilizing the information of the range space of between-class scatter matrixSband within-class scatter matrixSwfor face identification. In recent years, many approaches have been brought to improve the DLDA algorithm. Song et al.[2]proposed a PD-LDA algorithm by introducing a parameterβto improve the recognition rate; however, the improvement is not obvious and the choice of parameterβis difficult. Paliwal and Sharma[4]developed an improved DLDA algorithm to improve classification accuracy for DNA datasets; however, it is improper to deal with high-dimensional data such as face recognition.

Dimension reduction and eigenvectors extraction corresponding to nonzero eigenvalues are the main tasks of the DLDA algorithm. To achieve the two tasks, Yu and Yang’s algorithm adopts the principal component analysis(PCA )method and EVD; Song and Paliwal’s[2,4]algorithms use singular value decomposition (SVD). All the algorithms mentioned above are computationally complex. In this paper, two improved DLDA algorithms are proposed to reduce the computational complexity of the conventional DLDA algorithm.

In this paper, we propose the DLDA/ESVD algorithm that directly uses economic singular value decomposition (ESVD) to reduce dimension and extract eigenvectors corresponding to nonzero eigenvalues. Then we further propose the DLDA/QR-ESVD algorithm that uses high-performance column pivoting orthogonal triangular (QR) decomposition to reduce dimension and ESVD to extract eigenvectors corresponding to nonzero eigenvalues. The proposed two algorithms are efficient and outperform the conventional DLDA algorithm in terms of computational complexity. In addition, the DLDA/QR-ESVD algorithm achieves better performance than DLDA/ESVD algorithm by processing high-dimensional low rank matrices.

1 Direct Linear Discriminant Analysis

A brief overview of the DLDA algorithm is presented here. The DLDA algorithm aims to find a projection matrix that diagonalizes both within-class scatter matrixSwand between-class scatter matrixSbsimultaneously. In the DLDA algorithm, within-class scatter matrixSwand between-class scatter matrixSbare defined as[6]

(1)

(2)

The precursors[3]HwandHbof the within-class scatter and between-class matrices in Eqs.(1) and (2) are

(3)

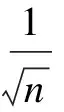
(4)

2 Proposed algorithms

First, the DLDA/ESVD algorithm is presented in detail, and then we further present the DLDA/QR-ESVD algorithm, which can obtain better performance than the DLDA/ESVD algorithm by processing a high-dimensional low rank matrix.

2.1 DLDA/ESVD algorithm

Hb=QbDbVb

(5)

(6)

(7)

Thus, it is easy to verify that

(8)

(9)

Since

2.2 DLDA/QR-ESVD algorithm

Hb=QbRbE

(10)

(11)

Then matrixRbcan be decomposed by the ESVD as

Rb=UbDbVb

(12)

where bothUbandVbare orthogonal matrix;Dbis a diagonal matrix; andUb∈Rr×r,Db∈Rr×r,Vb∈Rr×r.

Substituting Eq.(12) into Eq.(11), we obtain

Thus, it is easy to verify that

(13)

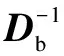
(14)

Since

3 Experiments

The experiments are used to verify the efficiency of the proposed two algorithms and the performance of the DLDA/QR-ESVD is better than that of the DLDA/ESVD by processing a high-dimensional low rank matrix. First, experiments for the DLDA/EVD, DLDA/ESVD and DLDA/QR-ESVD algorithms are conducted on ORL[8], FERET[9]and YALE[10]face databases. Secondly, the comparison testing between the DLDA/ESVD and the DLDA/QR-ESVD are conducted on random matrices. The experiments are tested on the PC with CoreTM2 Duo 2.99 GHz processor with 1.96 GB of RAM using Matlab 7.0 software.

3.1 Experiments on face databases

Tab.1 introduces three face databases in experiments, where Size stands for the number of all images in each database; Dimensions are the dimensionalities of image vectors; and Classes are the number of persons.

Tab.1 Description of three face databases

In each face database, the recognition rates and the training time of the DLDA/EVD, DLDA/ESVD and DLDA/QR-ESVD algorithms are tested. The recognition rates are used to evaluate the accuracy of the three algorithms. The training time is used to measure the computation time of each algorithm for dimension reduction and feature extraction, and the difference of the execution time in databases is mainly caused by the training time using different algorithms.

There are three main steps for testing the aforementioned algorithms. First, training sets are randomly selected from the face database, and the rest forms testing sets. Secondly, the training sets are trained to achieve dimension reduction and feature extraction using the above three algorithms under the same conditions, and the training time of each algorithm is recorded. Finally, both the training sets and the testing sets are projected into the optimal LDA subspace, and the nearest neighbor classifier based on the Euclidean distance is adopted to be the final classifier[11]. The final result we take is an average result of classification for 40 times based on cross-validation experiments.

Fig.1 shows the recognition rates on ORL, FERET and

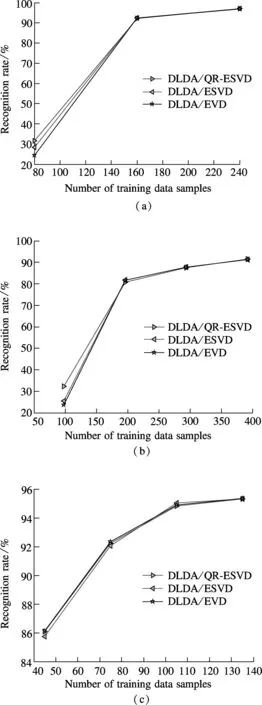
Fig.1 Recognition rates on different databases. (a) ORL face database; (b) FERET face database; (c) YALE face database

YALE face databases by using the DLDA/EVD, DLDA/ESVD and DLDA/QR-ESVD algorithms, respectively. It can be seen that the three algorithms achieve almost the same recognition rates on the three face databases under different numbers of training samples.

Fig.2 shows the training time on ORL, FERET and YALE face databases by using three algorithms respectively. It can be seen that the training times of the DLDA/ESVD algorithm and the DLDA/QR-ESVD algorithm are distinctly lower than those of the DLDA/EVD algorithm on the three face databases. The proposed two algorithms consume almost the same training time; the reason is that the rank of between-class matrixSbis approximately equal to the number of training sample classes (c≈r) on the three face databases.

Fig.2 Computation time on different databases. (a) ORL face database; (b) FERET face database; (c) YALE face database

3.2 Experiments on random data matrices

As it is difficult to find a public database with high-dimensional low rank data matrices to test the DLDA/ESVD and DLDA/QR-ESVD algorithms. Random data matrixH∈Rm×c(rank(H)=r) with variable dimensionsmfrom 5 000 to 10 000 are generated to verify the proposed two algorithms. Fig.3(a) shows that the proposed two algorithms can achieve similar computation time by processing high-dimensional full rank matrices (c=r=500). Fig.3(b) shows that the computation time of the DLDA/QR-ESVD algorithm is distinctly lower than that of the DLDA/ESVD algorithm by processing high-dimensional low rank matrices (r?c,c=800,r=200).

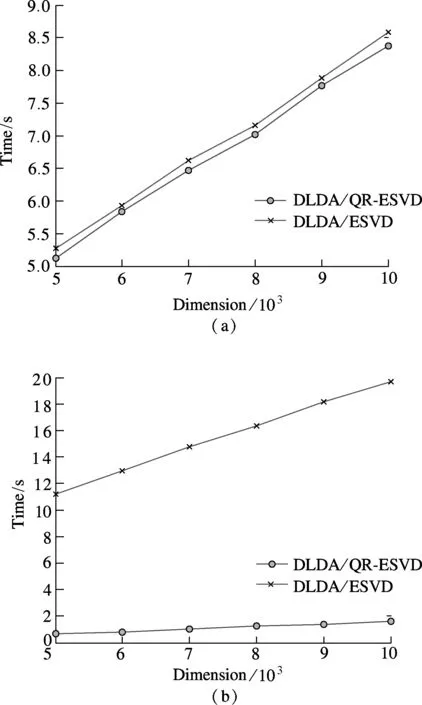
Fig.3 Computation time on random data matrices. (a) High-dimensional full rank matrices; (b) High-dimensional low rank matrices

4 Conclusion

In this paper, the DLDA/ESVD algorithm is proposed, which directly uses the ESVD to reduce dimension and extract eigenvectors corresponding to nonzero eigenvalues. Then we further propose the DLDA/QR-ESVD algorithm that uses high-performance column pivoting QR decomposition to reduce dimension and ESVD to extract eigenvectors corresponding to nonzero eigenvalues. The proposed two algorithms outperform the DLDA/EVD algorithm in terms of computational complexity and training time. The proposed two algorithms consume almost similar computation time by processing a high-dimensional full rank matrix (r=c). But the computation time of the DLDA/QR-ESVD algorithm is distinctly lower than that of the DLDA/ESVD algorithm by processing a high-dimensional low rank matrix (r?c).

It is worth exploring in two directions. First, since a computationally efficient way of reducing dimension is crucial in many fields of research, a number of applications of the DLDA/ESVD and DLDA/QR-ESVD algorithms should be envisaged. Secondly, the theoretical analysis of the proposed two algorithms should be further studied.

[1]Yu H, Yang J. A direct LDA algorithm for high dimensional data with application to face recognition [J].PatternRecognition, 2001,34(10): 2067-2070.

[2]Song F X, Zhang D, Wang J Z, et al. A parameterized direct LDA and its application to face recognition [J].Neurocomputing, 2007,71(1): 191-196.

[3]Joshi A, Gangwar A, Saquib Z. Collarette region recognition based on wavelets and direct linear discriminant analysis [J].InternationalJournalofComputerApplications, 2012,40(9): 35-39.

[4]Paliwal K K, Sharma A. Improved direct LDA and its application to DNA microarray gene expression data [J].PatternRecognitionLetters, 2010,31(16): 2489-2492.

[5]Ye J, Li Q. A two-stage linear discriminant analysis via QR-decomposition [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005,27(6): 929-941.

[6]Li R H, Chan C L, Baciu G. DLDA and LDA/QR equivalence framework for human face recognition[C]//The9thIEEEInternationalConferenceonCognitiveInformatics(ICCI). Beijing, China, 2010: 180-185.

[7]Golub G, Loan C,Matrixcomputations[M]. Baltimore, MD, USA: Johns Hopkins University Press, 1983: 170-236.

[8]Samaria F S, Harter A C. Parameterisation of a stochastic model for human face identification[C]//ProceedingsoftheSecondIEEEWorkshoponApplicationsofComputerVision. Los Alamitos, CA, USA,1994: 138-142.

[9]Phillips P J, Moon H, Rizvi S A, et al. The FERET evaluation methodology for face-recognition algorithms [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2000,22(10): 1090-1104.

[10]Georghiades A, Belhumeur P, Kriegman D. From few to many: illumination cone models for face recognition under variable lighting and pose [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2001,23(6): 643-660.

[11]Ye J, Janardan R, Park C H, et al. An optimization criterion for generalized discriminant analysis on undersampled problems [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2004,26(8): 982-994.