Bao Leping Fei Shumin Zhai Junyong

(Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education, Southeast University, Nanjing 210096, China)(School of Automation, Southeast University, Nanjing 210096, China)

During the last decade, the study of switched systems has attracted considerable attention due to its significance in both theoretical research and practical applications[1]. A switched system is a dynamical system described by a family of continuous-time subsystems and a rule that governs the switching between them. In many real cases, switched systems can be described by partial differential equations (PDE) or a combination of ordinary differential equations (ODE) and PDE, such as in chemical industry processes and biomedical engineering. We refer to these switched systems as distributed parameter switched systems (DPSS) or infinite dimensional switched systems[2-3]. The results of infinite dimensional dynamical switched systems are usually not straightforward, and they frequently require further analysis. Based on the fact that switched systems described by the PDE are more common in general, there is a realistic need to discuss such systems.

Analysis of switching sequences is a main research topic in the field of switched systems, and it plays an important role in the study of problems such as stability analysis and control design. The stability issues of switched systems include several interesting phenomena. It is well known and easy to demonstrate that switching between stable subsystems may lead to instability[4-6]. This fact makes stability and stabilization analysis of switched systems an important and challenging problem, which has received great attention[4-13]. Among them, there has been considerable growth of interest in using the dwell time approach to deal with switched systems[4,11,13].

On the other hand, there are several works concerning the infinite dimensional DPSS[14-21]. For example, Farra et al.[14]used Galerkin’s method to control synthesis for a quasi-linear parabolic equation, in which the state equation is fixed and the controller is switched. Sasane[15]generalized the finite dimensional switched system[8]to the infinite dimensional Hilbert space. Ref.[15] shows that when all the subsystems are stable and commutative pairwise, the switched linear system is stable under arbitrary switching via the common Lyapunov function. Hante et al.[18-19]gave necessary and sufficient conditions in terms of the the existence of the common Lyapunov function for the DPSS. Ouzahra[20]considered the feedback stabilization of the fixed distributed semilinear systems using switching controls which does not require the knowledge of the state of the system. Although much research has been done on stability and stabilization for switched systems, to the best of our knowledge, the control synthesis problem for the DPSS has not been extensively investigated.

Motivated by the above considerations, in this paper, we investigate control synthesis of the DPSS via the multiple Lyapunov function method. We use the semigroup theory due to the fact that it plays a central role and provides a unified and powerful tool for the study of the PDE systems[22]. The control design problem concentrates on the state feedback design problem. The main contribution of this paper is twofold. First, the controller is designed for the DPSS by applying the linear operator inequalities (LOIs) framework for the first time. Secondly, the sufficient conditions for exponential stabilization are derived in terms of the LOIs where the decision variables are operators in the Hilbert space, and the stabilization properties depend on the switching rule, while the existing work aims at unswitched distributed parameter systems. Being applied to heat switched propagation equations with the Dirichlet boundary conditions, the LOIs are subsequently reduced to standard linear matrix inequalities (LMIs), which has the advantage of being numerically well tractable by using the Matlab software. Compared with Ref.[21], it should be pointed out that our stabilization conditions completely depend on the system parameters and boundary data.

1 Preliminaries and Problem Formulation

LetH,Ube separable Hilbert space with the inner product 〈·,·〉. Notation ‖·‖ denotes the usual norm onH. LetL(U,H) denote the space of the bounded linear operator fromUtoH, andL(H) denotes the space of the bounded linear operator fromHtoH.Istands for the identity operator onHor appropriate dimensional identity matrix.

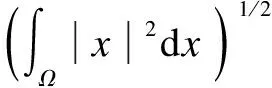
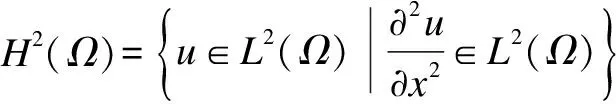
Definition1[23]LetP:H→Hwith a dense domainD(P)?Hbe self-adjoint, thenP≥0 (positive) if

〈Px,x〉≥0 ?x∈D(P)

(1)

whereP>0 (strictly positive), iff it is self-adjoint in the sense thatP*=Pand there exists a constantm>0, such that

〈Px,x〉≥m‖x‖2?x∈D(P)

(2)

A0≤0,A0<0 mean that-A0≥0,-A0>0, respectively.

Definition2An operatorM∈L(H) is called invertible if there exists an operatorN∈L(H) such thatMN=NM=I. We writeN=M-1to denote the inverse of operatorM.

(3)

We consider a general form of the linear distributed parameter switched control system

(4)

with the initial condition

x(t0)=x0

(5)

wherex∈His the state of the system;u∈Uis the control.σ:[t0,∞)→Θis the switching signal mapping time to some finite index setΘ={1,2,…,m}, and the switching signalσis a piecewise constant. The discontinuities ofσare called switching times or switches.

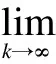
tk-tk-1≥τd?k∈N

(6)

whereτd>0 is the dwell time.

The objective of this paper is concerned with the control synthesis problem for switched systems (4) and (5). The control synthesis is related to the design of a switched state feedback control

u(t)=Kσ(t)x(t)

(7)

which ensures the exponential stability of the closed-loop DPSS

(8)

under some switching law, whereK1,K2,…,Kmare a family of gain operators to be determined.

2 Exponential Stabilization Analysis for DPSSunder Dwell Time Constraints

In this section, the exponential stabilization condition for the switched control system is extended to the distributed parameter system in the Hilbert space.

Without loss of generality, we make the following assumptions.

Assumption11) The state of the DPSS (8) does not jump at switching instants; i.e., the trajectoryx(t) is everywhere continuous. Switching signalσ(t) has a finite switching number at any finite interval time.

2) Each operatorAi(i=1,2,…,m) generates analytical semigroupTi(t) and the domainD(Ai)?Hof the operatorAiis dense inH.

3) Operators satisfy the conditionsBi∈L(U,H) andKi∈L(H,U).

Choose the following multiple Lyapunov function candidate

V(x,t)=Vσ(t)(x,t)=〈Pσ(t)x(t),x(t)〉

(9)

for (8) in the corresponding Hilbert spaceD(Ai)(i=1,2,…,m), where operatorsPi:D(Ai)→HandPi>0 satisfy

γpi〈x,x〉≤〈Pix,x〉≤γPi〈x,x〉,x∈D(Ai)

(10)

for some positive constantsγpi,γPi.

Theorem1For a given constantβ>0, suppose that Assumption 1 holds, if there exist linear operatorsXi>0 andYisuch that the following LOIs

(11)

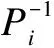
ProofSystems (4) and (5) with state feedback control (7) results in system (8). Suppose that Assumption 1 holds, from Corollary 5.2.4 of Ahmed[22], it can be proved that systems (5) and (8) have a unique classical solution for everyx0∈H, i.e., systems (5) and (8) turn to be well-posed on time interval [t0,∞) because the state does not jump at the switching instants.

Choosing the multiple Lyapunov function candidate for system (8) as the form of (9), whereVi=C(H×[t0,+∞),R+), and operatorsPisatisfying (10) and the following inequalities

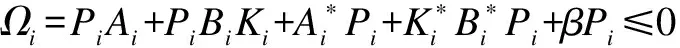
(12)

Fort∈[tk-1,tk), we can obtain

〈Pσ(tk-1)x(t),x(t)〉=V(t)≤γpσ(tk-1)‖x(tk-1)‖2

By using (10), it follows that

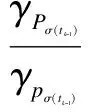
It is easy to calculate that

‖x(t)‖2≤μ‖x(tk-1)‖2≤
μe-β(t-tk-1)‖x(tk-1)‖2≤
μ2e-β(t-tk-1)e-β(tk-1-tk-2)‖x(tk-2)‖2≤
μ2e-β(t-tk-2)‖x(tk-1)‖2≤
?
μke-β(t-t0)‖x(t0)‖2

for allt≥t0and constantμ≥1. Noticing the fact that(k-1)τd≤t-t0, then

‖x(t)‖2≤μe-β(t-t0)e(k-1)ln μ‖x(t0)‖2≤
μe-(β-ln μ/τd) (t-t0)‖x(t0)‖2

(13)

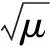
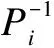
3 Application of Two Dimensional Switched HeatPropagation Systems

For the following switched heat propagation control system:

yt(x,y,t)=Dσ(t)2y(x,y,t)+Bσ(t)u(t)
(x,y,t)∈[0,]×[0,]×[t0,+∞)

(14)

Let the boundary value condition be

y(x,y,t)=0(x,y,t)∈?Ω×[t0,+∞)

(15)

The initial condition is

y(x,y,t0)=y0

(16)

We consider that the static state feedback is

u(t)=Kσ(t)y(t)

(17)

Ensure the exponential stability of the closed-loop DPSS to be

(18)

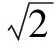
For a precise characterization of the class of the PDE systems considered in this paper, we formulate the system of Eq.(14) as an infinite dimensional system in the Hilbert spaceH=L2(Ω,Rn)) withHbeing the space of sufficiently smoothn-dimensional vector functions defined onΩthat satisfy the boundary condition (16).

Define the state functionxonHas

x(t)=y(·,·,t)t≥t0

(19)

the operatorsA1=D12=D1+D1,A2=D22=D2+D2; then Eq.(14) can be rewritten in the form of Eq.(4) and the first equation of (18) can be rewritten as Eq.(8), respectively, where the operatorAihas the dense domain

(20)

It is easily known that operatorsA1andA2generate analytical semigroupsT1(t) andT2(t), respectively, and system (18) has a unique classical solution[2].

The multiple Lyapunov function is chosen as

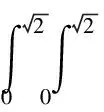
(21)

with positive constant diagonal matricesPi.

Differentiating (21), we find that

forx∈D(Ai).

BecausePi,Diare constant diagonal matrices, thenPiDi=DiPi.

Noticing thatPi,Diare positive diagonal matrices, we have

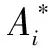
hold in correspondingx∈D(Ai)(i=1,2).

Integrating by part, according to the famous Green’s first identity and boundary condition (15), we can obtain the following inequalities

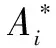
According to Poincare’s inequality (3), we can obtain

Then we have

provided that the following inequalities

(22)

are satisfied.

By the similar argument used in Theorem 1, it can be easily seen that (22) is equivalent to

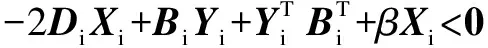
(23)

So, the following result is obtained.

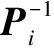
Remark2The idea of the LOIs is first applied to the study of distributed parameter systems in Refs.[25-26]. As it is shown, these LOIs are subsequently reduced to standard LMIs, which provide a new insight into the control theory of distributed parameter systems. Inspired by the above works, we utilize LOIs to the DPSS for the first time, and generalize the stability result of ODE switched systems[4]to the DPSS.

4 Examples

In this section we consider two examples to illustrate the proposed results.

Example1Utilize Theorem 2 for the switched heat propagation Eq.(18) with

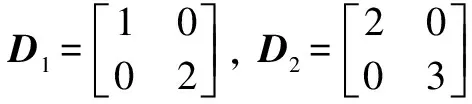
Letβ=0.5, by resolving LMIs (23), we obtain the state feedback matrices

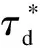
‖y(t)‖≤2.2095e-0.059 6(t-t0)‖y0‖

Example2Consider the switched heat propagation Eq.(18) with the following parameters:

Letβ=0.7, by resolving LMIs(23), we obtain the state feedback matrices:

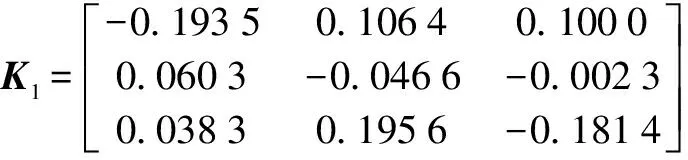
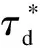
‖y(t)‖≤1.7432e-0.422 2(t-t0)‖y0‖

5 Conclusion

In this paper, based on the semigroup and operator theory, some sufficient conditions of exponential stabilization for a class of linear DPSS are derived in a LOIs framework. We transform the LOIs into the LMIs, which has the advantage of being numerically well tractable by using the Matlab software. The control synthesis is investigated by means of the multiple Lyapunov approach. Finally, two examples are given to illustrate the effectiveness of the proposed results.

[1]Lin H, Antsaklis P J. Stability and stabilizability of switched linear systems: a survey of recent results [J].IEEETransAutomatControl, 2009,54(2): 308-322.

[2]Curtain R F, Zwart H.Anintroductiontoinfinitedimensionallinearsystemtheory[M]. New York: Springer, 1995.

[3]Luo Z H, Guo B Z, Morgul O.Stabilityandstabilizationforinfinitedimensionalsystemswithapplications[M]. London: Springer, 1999.

[4]Liberzon D.Switchinginsystemsandcontrol[M]. Boston: Birkhauser, 2003.

[5]Liberzon D, Morse A S. Basic problems in stability and design of switched systems [J].IEEEContrSystMag, 1999,19(10): 59-70.

[6]Decarlo R A, Branicky M S, Pettersson S, et al. Perspectives and results on the stability and stabilizability of hybrid systems[J].ProceedingsofIEEE, 2000,88(7): 1069-1082.

[7]Sun Z, Ge S S.Switchedlinearsystems:controlanddesign[M]. Berlin: Springer-Verlag, 2004.

[8]Narendra K S, Balakrishnan J. A common Lyapunov function for stable LTI systems with commuting A-matrices [J].IEEETransAutomatControl, 1994,39(12): 2469-2471.

[9]Branicky M S. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems [J].IEEETransAutomatControl, 1998,43(4):186-200.

[10]Cheng D, Guo L. Stabilization of switched linear systems [J].IEEETransAutomatControl, 2005,50(5): 661-666.

[11]Geromel J, Colaneri P. Stability and stabilization of continuous time switched linear systems [J].SIAMJournalonControlandOptimization, 2006,45(5):1915-1930.

[12]Chen Y, Fei S, Zhang K, et al. Control of switched linear systems with actuator saturation and its applications [J].MathematicalandComputerModelling, 2012,56(1/2): 14-26.

[13]Allerhand L, Shaked U. Robust stability and stabilization of linear switched systems with dwell time [J].IEEETransAutomatControl, 2011,56(2): 381-386.

[14]Farra N, Christofides P. Coordinating feedback and switching for control of spatially distributed processes [J].ComputersandChemicalEngineering, 2004,28(1/2): 111-128.

[15]Sasane A. Stability of switching infinite-dimensional systems [J].Automatica, 2005,41(1): 75-78.

[16]Michel A, Sun Y. Stability of discontinuous cauchy problems in Banach space [J].NonlinearAnalysis, 2006,65(9): 1805-1832.

[17]Prieur C, Girard A, Witrant E. Lyapunov functions for switched linear hyperbolic systems [C]//The4thIFACConferenceonAnalysisandDesignofHybridSystems. Eindhoven, Netherlands, 2012:382-387.

[18]Hante F, Sigalotti M. Converse Lyapunov theorems for switched systems in Banach and Hilbert Spaces [J].SIAMJournalonControlandOptimization, 2011,49(2): 752-770.

[19]Amin S, Hante F, Bayen A. Exponential stability of switched linear hyperbolic initial-boundary value problems [J].IEEETransAutomatControl, 2012,57(2): 291-301.

[20]Ouzahra M. Global stabilization of semilinear systems using switching controls [J].Automatica, 2012,48(5): 837-843.

[21]Dong X, Wen R, et al. Feedback stabilization for a class of distributed parameter switched systems with time delay [J].JournalofAppliedSciences—ElectronicsandInformationEngineering, 2011,29(1):92-96.

[22]Ahmed N U.Semigrouptheorywithapplicationstosystemandcontrol[M]. New York: Longman Scientific Technical, 1991.

[23]Tucsnak M, Weiss G.Observationandcontrolforoperatorsemigroups[M]. Basel: Birkhauser Verlag, 2009.

[24]Chen Z.Partialdifferentialequations[M].2nd Ed. Beijing: University of Science and Technology of China Press, 2002. (in Chinese)

[25]Fridman E, Orlov Y. Exponential stability of linear distributed parameter systems with time-varying delays [J].Automatica, 2009,45(1):194-201.

[26]Tai Z, Lun S. Absolute mean square exponential stability of Lur’e stochastic distributed parameter control systems [J].AppliedMathematicsLetters, 2012,25(3): 115-119.