Liu Sifeng,Hu Mingli,Forrest Jef frey,2,Yang Yingjie,3

(1.Institute for Grey Systems Studies,Nanjing University of Aeronautics and Astronautics,Nanjing,211106,P.R.China;2.Mathematics Department,Slippery Rock University,Slippery Rock,PA 16057,USA;3.Centre for Computational Intelligence,De M ontfort University,Leicester,LE1 9BH,UK)

INTRODUCTION

In 1982,Deng Julong first proposed the grey system theory[1]. It focuses on the study of problems involving small samples and poor information and deals with uncertain systems with partially known information through generating, excavating and extracting useful information from what is available.In the natural world,uncertain systems with small samples and poor information exist commonly[2-3]. That fact determines the wide range of applicability of grey system theory.

A computer software on most of grey systems modeling can be downloaded from the web site of Institute for Grey System Studies of Nanjing University of Aeronautics and Astronautics(http://igss.nuaa.edu.cn)for free[4].

1 BASICSOF GREY SYSTEMS

Many systems in studies are named after the features of the research objects, while grey systems are labeled by the color of the research objects. For instance, Ashby referred objects with unknown internal information as black boxes.We use ″black″to indicate the unknown information, ″white″for the completely known information,and ″grey″for the partially known and partially unknown information.Accordingly,systems with completely known information are regarded as white, those with completely unknown information as black,and those with partially known and partially unknown information as grey.Here,the term ″system″is used to indicate the studies of the structure and function of the concerned object through analyzing the existing organic connections among the object,the relevant factors,the environment,and the related change laws[5-11].

Def in ition 1 Grey interval number

The f

ollowing equation

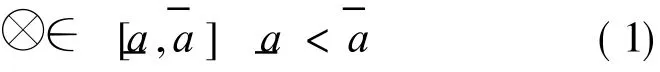
is called a grey interval number,or a grey interval for short,whereandare the upper and lower limits of the information separately[12]. The arithmetic of grey interval is very similar to the interval values[13].But a grey interval is the only one number which belongs to interval＜.It is different from an interval.

Def inition 2 General grey number

Let g±∈ R be an unknown real number within a union set of closed or open grey intervals,shown as

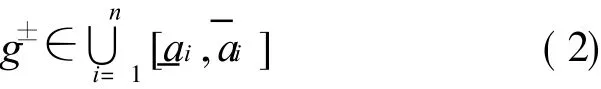
where i=1,2,… ,n,n is an integer and 0＜n＜∞,,for any grey interval,? i∈

±,then g is called a general grey number.g-=and g+=

are called the lower and upper limits of g±[14].

In practice,grey numbers can be represented in different forms, such as interval grey numbers,sets of discrete numbers,kernels and reduced form,etc.[15-17].

The operation rules of general grey numbers can be defined as operation rules of real numbers,but the degree of greyness of operation result should be considered carefully[18].

2 SEQUENCE GENERATION

Different from the stochastic theory that investigates statistical laws on the basis of probabilities established on prior knowledge,the grey system theory uncovers the change laws by excavating and organizing the available raw data,representing an approach to finding data out of data,which is referred to as grey sequence generation[12,19-20].

Def in ition 3 Sequence operator[17]

Assume that X is a sequence of numbers,and D a symbol of a series operations to work on X such that after applying D,the sequence X becomes XD=(x(1)d,x(2)d,…,x(n)d),where D is referred to as the first order sequence operator,XD as the first order sequence worked on by the operator D.

If D1,D2and D3are all sequence operators,D 1D2 is referred to as the second order sequence operator,and its application on X produces the second order sequence XD1D2=(x(1)d1d2,x(2)d 1d 2,…,x(n)d 1d 2).Similarly,D1D2D3 is referred to as the third order sequence operator and XD1D2D3=(x(1)d1d2d3,x(2)d1d2d3,…,x(n)d 1d 2d 3)is the third order sequence.

The most important sequence operator is the accumulating generation operator,which is the basis to build the widely applied GM(1,1).

Definition 4 Accumulating generation operator

Assume that X(0)=(x(0)(1),x(0)(2),…,x(0)(n))is an original sequence,D is a sequence operator to work on X(0), the first order sequence X(0)D=(x(0)(1)d,x(0)(2)d,…,x(0)(n)d)is defined as

where N+n is a set of all integers from 1 to n,then D is called an accumulating(generation)operator[12].

3 GREY INCIDENCE ANALYSIS

In the study of a complex system,many factors are involved,and the system represents the mutual interactions of these factors that determine its behavior.Grey incidence analysis[12]provides a new method to analyze which factors have primary influence,and which have less influence,on thedevelopment of the system[21-24].

Several different models of grey incidence analysis have been put forward,such as the model of degree of grey incidence defined by Professor Deng Julong[12],the model of absolute degree of grey incidence[2],the model of relative degree of grey incidence[2],the model of synthetic degree of grey incidence[2],the grey incidence models based on similarity and nearness[21],and so on.The most commonly used model is the model of absolute degree of grey incidence[25-29].

Def inition 5 Absolute degree of grey incidence

Let Xi,i∈N+2 be two sequences with the same length that is defined as the sum of the distances between two consecutive time moments,shown as

Then

is referred to as the absolute degree of grey incidence between X 1 and X2.

4 GREY CLUSTER EVALUATION MODEL

The grey cluster evaluation model is mainly applicable to checking whether or not the observational objects belong to pre-determined classes such that they can be treated differently.The grey cluster model with variable weight[12],the grey cluster model with fixed weight[23],the grey cluster model based on endpoint triangular whitenization functions[23],and the grey cluster model based on center-point triangular whitenization functions are the commonly used grey cluster evaluation models based on whitenization weight functions[30].

Assume that n objects are clustered into s different grey classes according to m criteria.The observed value of object i in terms of criterion j is xij,i∈The object i needs to be evaluated and diagnosed based on xij. The particular computational steps of the grey evaluation model based on endpoint triangular whit enization functions are as follows.

Step 1 Based on the predetermined number s of grey classes for the planned evaluation,divide the each ranges of the criteria into s grey classes.For example,let[a1,as+1]be the range of the values of criterion j.Now,divide[a1,as+1]into s grey classes as follows

[a1,a2],… ,[ak-1,ak],… ,[as-1,as],[as,as+1]where ak,k∈ N+s+1,in general,can be determined based on specific requirements of a situation or relevant qualitative analysis.

Step 2 Calculate the geometric midpoint between the various cells,λk=(ak+ ak+1)/2,k∈

Step 3 Let the whitenization weight function value forλk to belong to the k th grey class be 1.When(λk,1)is connected to the starting pointλk-1 of the(k-1)th grey class and the ending pointλk+1 of the(k+ 1)th grey class,a triangular whitenization weight function fkj(?)is obtained in terms of criterion j about the k th grey class,j∈ N+m,k∈ N+s.For f1j(? )and fsj(? ),the range of criterion j can beex tended to the left to a0 and to the right to as+2,respectively(Fig.1).

For an observed value x of criterion j,its de-gree

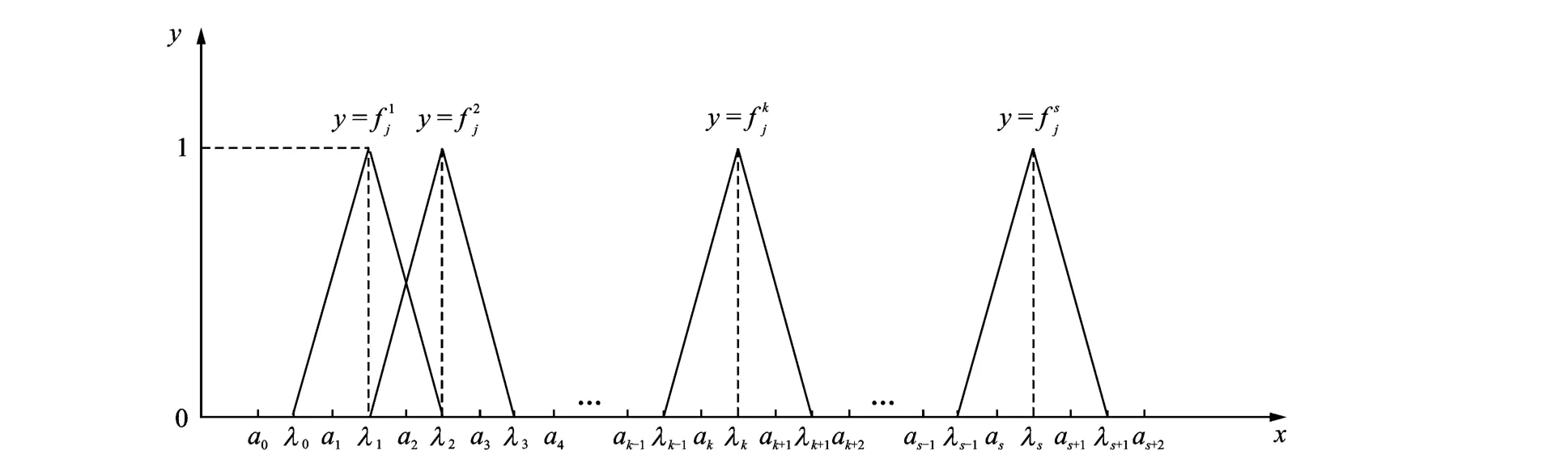
Fig.1 General endpoint triangular whitenization weight function

5 GREY PREDICTION MODEL

Step 4 Compute the comprehensive clustering coefficient for object i with respect to grey class k,that is

The computational steps of the grey cluster model based on center-point triangular whiten ization functions are mainly common but different form the following Step 1.

Step 1 Based on the s grey classes required by the evaluation task,respectively,determine the centersλ1,λ2,… ,λs-1,andλs of thegrey class 1,2,…,s-1,and s.

The centers stand for the particular points for the observed values to belong to particular grey classes,and they could be either the centers of their individual interval or not.Also,the field of each criterion is correspondingly divided into s grey classes,which are represented respectively using their centersλk,k∈

The grey cluster evaluation model based on end-point triangular whitenization weight functions is applicable to the case that the boundary of each grey class is clear but the most possible point of each grey class is unknown.The grey cluster evaluation based on center-point triangular whiten ization weight functions is applicable to the case that the most possible point of each grey class is known but the boundary of each grey class is unclear.

Grey prediction models can be used to predict the future behavior of system variables with small samples.Based on the practical circumstances,various grey prediction models such as GM(1,1),remnant GM(1,1),GM(0,N),and power GM(1,1) models, can be used. The most commonly used model in grey system theory for prediction of sequences is GM(1,1)[1,19,31-36].

Definition 6 Model GM(1,1)

Assume that X(0)=(x(0)(1),x(0)(2),…,x(0)(n))is a sequence of raw data which satisfy the law of grey exponent,X(1)=(x(1)(1),x(1)(2),… ,x(1)(n)),n ≥ 4,is its accumulation generated sequence,and Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))is the sequence generated from X(1)by adjacent neighbor means,where z(1)(k)=(x(1)(k)+ x(1)(k-1)),k=2,3,…,n.Then,x(0)(k)+ az(1)(k)=b is referred to as the model GM(1,1),where the symbol GM(1,1)stands for″the first order grey model with one variable″[12].

Assume that X(0)is non-negative.(a,b)Tis the sequence of parameters in model GM(1,1),then theleast square estimate sequence of the model GM(1,1)satisfies(BTB)-1BTY,where

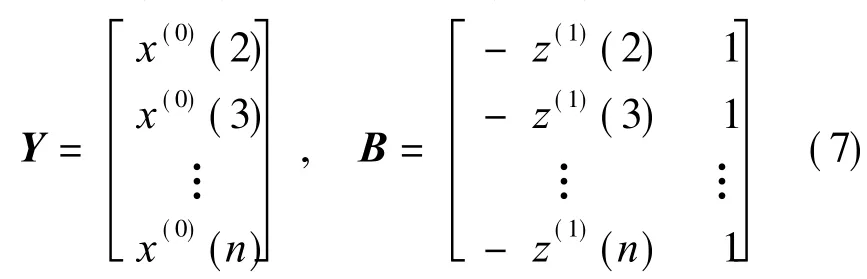
Example 1 Given a sequence of raw data X(0)=(x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5))=(2.874, 3.278, 3.337, 3.390, 3.679),simulate this sequence X(0)by GM(1,1).

Solution X(1)=(x(1)(1),x(1)(2),x(1)(3),x(1)(4),x(1)(5))=(2.874,6.152,9.489,12.897,16.558)

Z(1)=(z(1)(2),z(1)(3),z(1)(4),z(1)(5))=(4.513,7.820,11.184,14.718)

Therefore

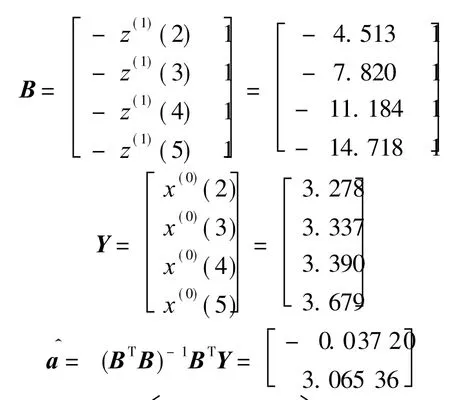
The sequence of errors is

X(k)=X(0)(k)-(k)=(0,0.046,- 0.017 5,- 0.091 7,0.065 4)

6 GREY MODELS FOR DECISION-MAKING

Grey decision-making is about making decision using such decision models that involve grey elements or combine the general decision model and grey system models.The emphasis of grey decision-making is the study on the problem of choosing a specific scheme.

Def inition 7 Scheme

Assume that A={a1,a2,… ,an}with ai,i∈N+n

? as the i th event,is the set of all events within the range of a study,and B={b1,b2,…,bm}with bj,j∈N+m as the j th countermeasure,is the set of all possible countermeasures. Then the Cartesian product S=A× B={(ai,bj)|ai∈ A,bj∈B}is called a schemes set,where each ordered pair sij=(ai,bj),for ai∈ A and bj∈ B,is called a scheme[12].

For a given scheme sij∈ S,evaluating the effects under a set of pre-determined objectives and deciding based on the evaluation on what to take and what to let go is the decision-making.

Definition 8 Grey target

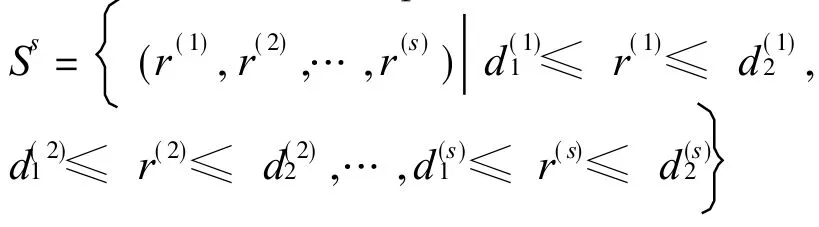
is called a grey target of a s-dimensional decisionmaking. Similarly,we can define satisfactory effect vector,desirable scheme and desirable countermeasure with respect to objectives 1,2,…,and s.

The weighted multi-attribute grey target decision model is presented as follows.

Definition 9 Effect measure[37]

(1)Let k be a benefit type objective,that is,for k the larger the effect sample value is the better,and the decision grey target of objective kthat is,stands for the threshold effect valueof objective k.Then

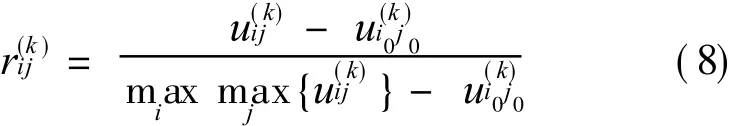
is referred to as the effect measure of a benefittype objective.

(2)Let k be a cost type objective,that is,for k the smaller the effect value is the better,and thedecision grey target of objective k is,that is,stands for the threshold effect value of objective k.Thenis referred to as the effect measure of cost type objective.

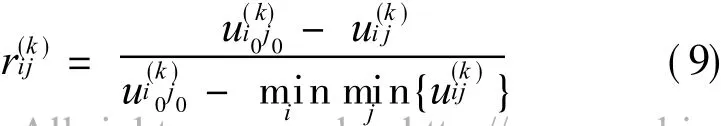
(3)Let k bea moderate-value typeobjective,that is,for k the closer to a moderatevalue A the effect value is the better,and the decision grey target of objective k isthat is,both A-are respectively the lower and upper threshold effect values of objective k.Then

is referred to as the lower effect measure of moderate-value type objective.(ii)When u(k)ij∈ [A,A+],then

is referred to as the upper effect measure of moderate-value type objective.

The effect measures of benefit type objectives represent the degrees of both how close the effect sample values are to the maximum sample values and how far away they are from the threshold effect values of the objectives. Similarly,the effect measures of cost type objectives represent the degrees of how close the effect sample values are to the minimum effect samplevalues and how far away the effect sample values are from the threshold effect values of the objectives. The lower effect measures of moderate value type objectives represent the degrees of both how close the effect sample values which are smaller than the moderatevalue A are to the moderate value A and how far away they are from the lower threshold effect value of the objectives,and the upper effect measures of moderate value type objectives represent the degrees of both how close the effect samplevalues which are larger than the moderate value A are to them oderatevalue A and how far away hey are from the upper threshold effect value of the objectives.

For the situation of undershoot,it can also correspondingly be divided into the following four kinds:

(1) The effect value of a benefit-type objective is smaller than the threshold valuethat is,

(2)The effect value of a cost-type objective is larger than the threshold valuethat is,

(3)The effect value of a moderate-value type objective is smaller than the lower threshold effect value A-that is,

(4)The effect value of a moderate-value type objective is larger than the upper threshold effect value A+that is,

In order to make the effect measures of each type objective satisfy the condition of normality,that is,-1,1],without loss of generality,we can assume that:

(1) For a benefit type objective,-mia x mja x

(2) For a benefit type objective,-miinmji n

(3)For the situation that the effect value of a moderate-value type objective is smaller than the lower threshold effect value A-A-

(4)For the situation that the effect value of a moderate-value type objective is larger than the upper threshold effect value A+≤A+

Proposition 1 The effect measure(i=1,2,… ,n;j=1,2,… ,m;k=1,2,… ,s),as defined in Definition 9,satisfy the following properties:(1)are non-dimensional;(2)the more ideal the effect is,the largerare;(3)∈ [- 1,1].Therefore,are called the uniform effect measure.

For the situation of hitting the target,[0,1]; and for the situation of missing the target,

Definition 10 Synthetic effect measure

Assume that Z k stands for the decision weight of objectives k,k=1,2,…,s,and satisfiesis called a synthetic effect measure of the scheme sij,which is still denoted as rij=And R=(rij)n×m is known as the matrix of synthetic effect measures[37].

The weighted multi-attribute grey target decision can be made by the following steps:

Step 1 Based on the set A={a1,a2,…,an}of events and the set B={b1,b2,…,bm}of countermeasures,construct the set of schemes S={sij=(ai,bj)|ai∈ A,bj∈ B}.

Step 2 Determine the decision objectives k,k=1,2,…,s.

Step 3 Determine the decision weights Z1,Z2,…,Z s of the objectives.

Step 4 For each objective k,compute the corresponding observed effect matrix U(k)=(u(ijk))n×m.

Step 5 Determine the threshold effect value of objective k.

Step 8 Determine the optimum scheme si0j0.

Example 2 Select the supplier of key components of large commercial aircrafts by the weighted multi-attribute grey target decision model.

Solution The following five objectives are considered: quality,price, time of delivery,design proposal,and competitiveness.

Among these objectives,competitiveness,quality,and design proposal are qualitative.They are scored by relevant experts′evaluations satisfying that the higher evaluation scores are better.That is,they are benefit type objectives.Take the threshold value=9,k=1,4,5.For the objective of cost,the lower cost is better.Therefore,it is a cost type objective.Take the threshold value=15.The objective of″time of delivery″is one of moderate-value type.The main manufacturer desires the delivery at the end of the 16th month with allowed two-month deviation.That is,=2,the lower threshold effect value is 16- 2=14,and the upper threshold effect valueis 16+2=18.

The AHP method is used to determine the weights.The detailed procedure is omitted here and Table 1 shows the obtained weight for each objective.

Table 1 Evaluation system of objectives

The effect sample vectors of each of the objectives as follows

U(1)=(9.5,9.4,9)

U(2)=(14.2,15.1,13.9)

U(3)=(15.5,17.5,19)

U(4)=(9.6,9.3,9.4)

U(5)=(9.5,9.7,9.2)

Using the uniform effect measure,we have

R=[r 11,r12,r13]=[0.846 3,0.485 2,0.299 9]

Because r11＞ 0,r 12＞ 0,r13＞ 0,it means that all these threesuppliers havehit the target.From=0.846 3,it follows that the main manufacturer should sign the agreement with supplier 1.

7 CONCLUSION

The general grey numbers, the grey sequence operators and several most commonly used grey system models,such as the absolute degree of grey incidence model,the grey cluster model based on endpoint triangular whit enization functions,thegrey cluster model based on center-point triangular whiteniza tion functions,the grey prediction model of the model GM(1,1),and the weighted multi-attribute grey target decision model are introduced.From this paper,we can see that the research on grey methods and models remains in the ascendant.Related theories and practice achievements emerge endlessly[38-39].But as a new branch of systems science, it is unavoidable that there exist immature and imperfect parts in the grey system theory.The studies on grey analysis models,grey prediction models, grey decision-making models, grey control models and common high-dimensional models are all in progressing stage. A large number of practical and scientific problems in reality remain to be excavated,explored and solved. The testing and specific quantitative standards of grey models remain to be further studied.

[1] Deng Julong.Control problems of grey systems[J].Systems&Control Letters,1982,1(5):288-294.

[2] Vallee R.Book reviews:Grey information:Theory and practical applications[J].Kybernetes,2008,37(1):89.

[3] Andrew A M.Why the world is grey[J].Grey Systems:Theory and Application,2011,1(2):112-116.

[4]Zeng Bo,Liu Sifeng,Meng Wei.Development and application of MSGT 6.0(modeling system of grey theory 6.0)based on Visual C# and XML[J].Journal of Grey System,2011,23(2):145-154.

[5]Deng Julong.Several problems on the research and development of grey systems [C]//New Developments in Grey Systems Research.Wuhan:Press of Huangzhong University of Science and Technology,1996:1-12.(in Chinese)

[6]Gu Jifa,Xu Guozhi.Preface for grey systems theory and its application[M].2nd Edition.Beijing:Science Press,1999.(in Chinese)

[7]Haken H.Synegetics[M].2nd Edition.Berlin:Springer-Verlag,1978.

[8]Lin Yi,Liu Sifeng.Several programming models with unascertained parameters and their application[J].Journal of Multi-Criteria Decision Analysis,1999,8(1):206-220.

[9]Liu Sifeng,Forrest J.Onastray of complicated model for uncertain systems[J]. Systems Engineering-Theory& Practice,2011,31(10):1960-1965.(in Chinese)

[10]Pawlak Z.Rough sets[J].International Journal of Computer&Information Sciences,1982,11(5):341-356.

[11]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[12]Deng Julong.Grey control systems[M].Wuhan:Press of Huazhong University of Science and Technology,1985.(in Chinese)

[13]Alefeld G,Herzberger J.Introduction to interval computations[M].New York:Academic Press Inc,1983.

[14]Liu Sifeng,Fang Zhigeng,Yang Yingjie,et al.General grey numbers and its operations[J].Grey Systems:Theory and Application,2012,2(3):4-15.

[15]Liu Sifeng,Fang Zhigeng,Xie Naiming.Algorithm rules of interval grey numbers based on the″Kernel″and the degree of greyness of grey numbers[J].Systems Engineering and Electronics,2010,32(2):313-316.

[16]Yang Yingjie,Liu Sifeng.Reliability of operations of grey numbers using kernels[J]. Grey Systems:Theory and Application,2011,1(1):57-71.

[17]Liu Sifeng.The three axioms of buffer operator and their application[J].The Journal of Grey System,1991,3(1):39-48.

[18]Xie Naiming, Liu Sifeng. Novel methods on comparing grey numbers[J].Applied Mathematical Modelling,2010,4(2):415-423.

[19]Wei Yong,Kong Xinhai,Hu Dahong.A kind of universal constructor method for buff er operators[J].Grey System:Theory and Application,2011,1(2):178-185.

[20]Liu Sif eng.Axiom on grey degree[J].The Journal of Grey System,1996,8(4):397-400.

[21]Lin Yi.Liu Sifeng.A systemic analysis with data(I)[J].International Journal of General Systems,2000,29(6):989-999.

[22]Lin Yi,Liu Sifeng.A systemic analysis with data(II)[J].International Journal of General Systems,2000,29(6):1001-1013.

[23]Liu Sifeng,Guo Tianbang.Grey system theory and application[M].Kaifeng:Henan University Press,1991.

[24]Liu Sif eng,Xie Naiming,Forrest J.Novel models of grey relational analysis based on visual angle of similarity and nearness[J].Grey Systems: Theory and Application,2011,1(1):8-18.

[25]Liu Sifeng,Lin Yi.An introduction to grey systems theory[M].Grove City:IIGSSAcademic Publisher,1998.

[26]Liu Sifeng,Dang Yaoguo,Fang Zhigeng,et al.Grey system theory and application[M].5th Edition.Beijing:Science Press,2010.

[27]Liu Sifeng,Lin Yi. Grey systems: Theory and applications[M].London:Springer-Verlag,2011.

[28]Liu Sifeng,Lin Yi.Grey information: Theory and practical applications [M]. London: Springer-Verlag,2006.

[29]Zhang Ke,Liu Sifeng.Extended clusters of grey incidences for panel data and its application[J].Systems Engineering Theory& Practice,2010,30(7):1253-1258.(in Chinese)

[30]Liu Sifeng,Xie Naiming.A new grey evaluation method based on reformative triangular whitenization weight function[J].Journal of Systems Engineering,2011,26(2):244-250.(in Chinese)

[31]Wang Ziliang,Liu Sifeng. Trend testing of grey dynamic models[C]//2004 IEEE International Conference on Systems, Man and Cybernetics.Alaska,USA:IEEE,2004:2438-2442.

[32]Xiao Xinping,Peng Kunkun.Research on generalized non-equidistance GM(1,1)model based on matrix analysis[J].Grey Systems:Theory and Application,2011,1(1):87-96.

[33]Li Qiaoxing,Liu Sifeng,Lin Yi.Grey enterprise input-output analysis[J].Journal of Computational and Applied Mathematics,2012,236(7):1862-1875.

[34]Xie Naiming,Liu Sifeng.Discrete grey forecasting model and its optimization[J].Applied Mathematical Modelling,2009,33(2):1173-1186.

[35]Cui Jie,Zeng Bo.Study on parameters characteristics of NGM(1,1,k)prediction model with multiplication transformation[J]. Grey Systems: Theory and Application,2012,2(1):24-35.

[36]Yao Tianxiang,Forrest J,Gong Zaiwu.Generalized discrete GM(1,1)model[J].Grey Systems:Theory and Application,2012,2(1):4-12.

[37]Liu Sifeng,Yuan Wenfeng,Sheng Keqin.Multiattribute intelligent grey target decision model[J].Control and Decision,2010,25(8):1159-1163.(in Chinese)

[38]Scarlat E,Delcea C.Complete analysis of bankruptcy syndrome using grey systems theory[J]. Grey Systems:Theory and Application,2011,1(1):19-32.

[39]Delcea C,Scarlat E.The diagnosis of firm’s″diseases″using thegrey systems theory methods[M].Edited by Liu Sifeng,Lin Yi.London:Springer-Verlag,2010:105-119.