羅美菊, 吳歐

(1.遼寧大學(xué)數(shù)學(xué)院,遼寧 沈陽 110036;2.中國人民解放軍理工大學(xué)理學(xué)院,江蘇 南京 210007)

求解廣義納什均衡問題的增量罰算法

羅美菊1, 吳歐2

(1.遼寧大學(xué)數(shù)學(xué)院,遼寧 沈陽 110036;2.中國人民解放軍理工大學(xué)理學(xué)院,江蘇 南京 210007)

研究每個(gè)局中人的決策集都有可能與競爭者的決策集有關(guān)的廣義納什均衡問題.給出了該廣義納什均衡問題罰函數(shù)形式的再定式.通過分析其KKT點(diǎn)的特點(diǎn),進(jìn)一步給出了求解廣義納什均衡問題的增量罰算法.

廣義納什均衡問題;罰函數(shù);KKT條件;算法

1 引言

廣義納什均衡問題(generalized Nash equilibrium problem簡記為GNEP)是標(biāo)準(zhǔn)的納什均衡問題的一種推廣.它考慮每個(gè)局中人的決策集都有可能與競爭者的決策集有關(guān)的情形.最早的關(guān)于GNEP的研究在1952年由文獻(xiàn)[1]給出.此后,在1965年文獻(xiàn)[2]中考慮了所有局中人的決策都滿足相同的約束條件的GNEP.此外,1991年文獻(xiàn)[3]運(yùn)用變分不等式或擬變分不等式再定式的方法考慮了GNEP.廣義納什均衡問題在實(shí)際中有著廣泛的應(yīng)用.特別地,近期關(guān)于GNEP的研究大部分都集中在工程應(yīng)用上[45],主要目的是從博弈論的觀點(diǎn)得到更好的平衡系統(tǒng).

關(guān)于GNEP,對(duì)于不同的目標(biāo)函數(shù)和問題集目前已有很多方法對(duì)其求解.其中比較著名的是將GNEP表示成擬變分不等式問題[3,6],再進(jìn)一步求解.此外,通過引入擬變分不等式問題的價(jià)值函數(shù),也可將GNEP再定式為最小值為零的最優(yōu)化問題[7],進(jìn)而應(yīng)用全局優(yōu)化方法求解.亦可通過罰函數(shù)方法把GNEP轉(zhuǎn)化成一系列納什均衡問題,然后給出該納什均衡問題變分不等式形式的再定式,進(jìn)而對(duì)其求解[6,8].

本文提出了一種新的求解GNEP的方法–增量罰函數(shù)方法.利用該方法在一定條件下能得到合理的GNEP的解.

2 廣義納什均衡問題

本文考慮有N個(gè)局中人的非合作博弈問題.以后把第v個(gè)局中人簡單的記作v.用nv維向量xv表示局中人v的策略,其中nv為正整數(shù).將所有局中人的策略用向量

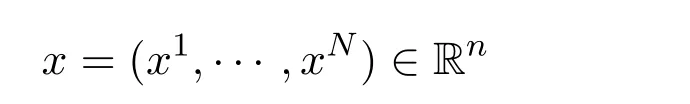
3 廣義納什均衡問題的再定式

4 求解廣義納什均衡問題的增量罰算法

[1]Debreu G.A social equilibrium existence theorem[J].Proceedings of the National Academy of Sciences, 1952,38:886-893.

[2]Rosen J B.Existence and uniqueness of equilibrium points for concave N-person games[J].Econometrica, 1965,33:520-534.

[3]Harker P T.Generalized Nash games and quasi-variational inequalities[J].European Journal of Operational Research,1991,54:81-94.

[4]Kesselman A,Leonardi S,Bonifaci V.Game-theoretic analysis of internet switching with sel fi sh users[J]. Proceedings of the First International Workshop on Internet and Network Economics,WINE,Lecture Notes in Computer Science,2005,3828:236-245.

[5]Pang J S,Scutari G,Facchinei F,et al.Distributed power allocation with rate constraints in Gaussian parallel interference channels[J].IEEE Transactions on Information Theory,2008,54:3471-3489.

[6]Pang J S,Fukushima M.Quasi-variational inequalities,generalized Nash equilibria,multi-leader-follower games[J].Computational Management Science,2005,2:21-56.

[7]Fukushima M.A class of gap functions for quasi-variational inequality problems[J].Journal of Industrial and Management Optimization,2007,3:165-171.

[8]Facchinei F,Pang J S.Large-Scale Nonlinear Optimization[M].Heidelberg:Springer-Verlag,2006.

Incremental penalty method for solving generalized NASH equilibrium problem

Luo Meiju1,Wu Ou2
(1.School of Mathematics,Liaoning University,Shenyang 110036,China;
2.College of Science,PLA University of Science and Technology,Nanjing 210007,China)

This paper is concerned with the generalized Nash equilibrium problem(GNEP),in which each player′s strategy set may depend on the rival players′strategies.We then propose a penalized reformulation for GNEP.Furthermore,we present an incremental penalty method for solving GNEP by analysis characteristic of the KKT points.

generalized Nash equilibrium problem,penalty function,KKT condition,algorithm

O225

A

1008-5513(2012)05-0599-05

2011-12-10.

遼寧大學(xué)青年基金(2011LDQN09).

羅美菊(1982-),博士,講師,研究方向：隨機(jī)均衡問題及其應(yīng)用.

2010 MSC:90C33