劉利群,陳祥恩

(1.長(zhǎng)江大學(xué)信息與數(shù)學(xué)學(xué)院,湖北 荊州 434023;2.西北師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,甘肅 蘭州 730079)

關(guān)于圖的鄰點(diǎn)可區(qū)別全色數(shù)的上界研究

劉利群1,陳祥恩2

(1.長(zhǎng)江大學(xué)信息與數(shù)學(xué)學(xué)院,湖北 荊州 434023;2.西北師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,甘肅 蘭州 730079)

圖G的鄰點(diǎn)可區(qū)別全染色是指G存在一個(gè)正常全染色f使得任意相鄰兩點(diǎn)有不同的色集合.本文主要研究鄰點(diǎn)可區(qū)別正常全色數(shù)的上界,目前鄰點(diǎn)可區(qū)別全染色的一個(gè)較好的上界是?+C+20,本文用概率方法改進(jìn)了這個(gè)結(jié)果,得到了鄰點(diǎn)可區(qū)別全色數(shù)的一個(gè)較小上界?+C+3.

鄰點(diǎn)可區(qū)別全染色;鄰點(diǎn)可區(qū)別全色數(shù);上界

1 引言

染色問(wèn)題是圖論中具有重要實(shí)際意義和理論意義的研究課題之一.1965年,Bahzad和Vizing各自獨(dú)立提出了圖的全染色的概念和猜想.2004年,文獻(xiàn)[1-2]提出了圖的鄰點(diǎn)可區(qū)別全染色的概念和猜想.文獻(xiàn)[3-4]對(duì)圖的全染色作了進(jìn)一步研究,得到了一些較好的結(jié)果.文獻(xiàn)[5]得到了鄰點(diǎn)可區(qū)別全染色的一個(gè)上界?+C+20.本文嘗試通過(guò)應(yīng)用局部引理,得到了鄰點(diǎn)可區(qū)別全色數(shù)的一個(gè)較小的上界?+C+3.

下面給出將要用到的一些概念與定理.

定義1[1]G(V,E)是階至少為2的連通圖,k是正整數(shù),f是從V(G)∪E(G)到{1,2,···,k}的一個(gè)映射.對(duì)任意u∈V(G),記

2 主要結(jié)果及證明

定理1 設(shè)G(V,E)是連通圖,若

證明 假設(shè)圖G(V,E)已給出,分以下四個(gè)步驟對(duì)圖G的邊進(jìn)行染色:

第一步由引理3,可先用?(G)+C種顏色對(duì)G進(jìn)行正常全染色.

第二步取一種新顏色a,對(duì)G的每個(gè)頂點(diǎn)隨機(jī)獨(dú)立的挑選它的一條關(guān)聯(lián)邊用新顏色a重染.這時(shí),邊e=uv被新顏色a重染的概率是

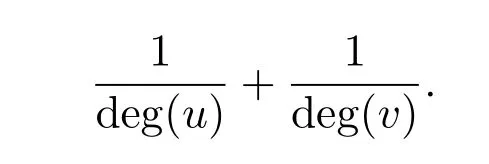
第三步在第二步完成后,另取一種新顏色b,再對(duì)G的每個(gè)頂點(diǎn)隨機(jī)獨(dú)立的挑選它的一條關(guān)聯(lián)邊用新顏色b重染.注意:新顏色b可能覆蓋新顏色a.

第四步在第三步完成后,另取一種新顏色c,再對(duì)G的每個(gè)頂點(diǎn)隨機(jī)獨(dú)立的挑選它的一條關(guān)聯(lián)邊用新顏色c重染.注意:新顏色c可能覆蓋新顏色a,b.

下面將證明以下兩點(diǎn)成立的概率為正:

1.著色仍然正常即沒(méi)有相鄰兩條邊或相鄰的兩點(diǎn)著色相同或相關(guān)聯(lián)的點(diǎn)與邊著色相同;

2.著色是鄰點(diǎn)可區(qū)別的即對(duì)任意兩點(diǎn)u,v∈V(G)(1≤d(u,v)≤2),有C(u)?=C(v).為此,定義如下壞事件:

(I)對(duì)每對(duì)相鄰的邊{e,f∈E(G)},令A(yù)e,f表示e和f被染成同種顏色的事件.

(II)對(duì)每一條邊

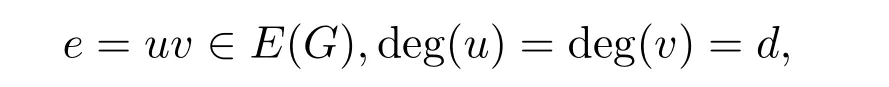
令Bu,v表示u和v的關(guān)聯(lián)邊是正常著色且C(u)=C(v)的事件.

下面證明上述事件都不發(fā)生的概率為正.

構(gòu)造相關(guān)圖D,其中D的頂點(diǎn)是以上二種類型的所有事件,設(shè)EX,EY是D的兩個(gè)頂點(diǎn)(每個(gè)X,Y是一對(duì)相鄰邊,或者是和一條邊相鄰的所有邊及其這條邊本身.EX和EY是相鄰的當(dāng)且僅當(dāng)X和Y至少包含一條公共邊.由于EX的每個(gè)事件發(fā)生依賴于X的邊,從而D是事件的相關(guān)圖.

首先,需要計(jì)算每個(gè)壞事件發(fā)生的概率,有以下三條成立:

1)對(duì)類型(I)的每個(gè)事件Ae,f,有

[1]張忠輔,陳祥恩,李敬文,等.關(guān)于圖的鄰點(diǎn)可區(qū)別全染色[J].中國(guó)科學(xué):A輯,2004,34(5):577-583.

[2]Zhang Zhongfu,Chen X iang′en,Li Jingwen,et al.On the ad jacent vertex distinguishing total coloring of graph[J].Science in China:Ser A,2005,48(3):289-299.

[3]Zhang Zhongfu,Yao Bing.A note on the ad jacent vertex distinguishing total chromatic number of graph[J]. Journal of Lanzhou Jiaotong University:Natural Science,2006,23(6):143-145.

[4]M olloy M,Reed B.A bound on the total chromatic number[J].Combinatorica,1998,18:241-280.

[5]晁福剛,張忠輔,強(qiáng)會(huì)英.圖的鄰點(diǎn)可區(qū)別全色數(shù)的一個(gè)上界[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2010,26(1):91-95.

[6]A lon N,Spencer J.The Probabilistic Method[M].New York:W iley,1992.

[7]M olloy M,Reed B.G raph Coloring and the Probabilistic M ethod[M].New York:Springer,2002.

[8]Yap H P.Total Coloring of G raphs[M].New York:Springer,1996.

[9]Bondy J A,M urty U SR.G raph Theory with App lications[M].London:London M acm illan Press,1976.

[10]Dietel R.G raph Theory[M].New York:Springer,1997.

On an upper bound for ad jacen t vertex d istinguish ing total ch rom atic num ber of graphs

Liu Liqun1,Chen Xiang′en2

(1.College of In form ation and M athem atics,Yangtze University,Jingzhou 434023,China; 2.College of M athem atics and In form ation Science,Northwest Norm al University,Lanzhou 730079,China)

A proper total coloring of the graph G is called ad jacent vertex distinguishing total coloring,for any two ad jacent vertices u,v∈V(G),we have C(u)?=C(v),where C(u)is called color set of vertex u.Inthis paper, we study the upper bound on the ad jacent vertex distinguishing total chromatic number.Δ+C+20is a good conclusion of the upper bound on the ad jacent vertex distinguishing total chrom atic number of graphs up till now.By probability m ethod,we obtained the conclusion that a upper bound on the ad jacent vertex distinguishing total chrom atic number isΔ+C+3 in som e condition in this paper.

ad jacent vertex distinguishing total coloring,ad jacent vertex distinguishing total chrom atic number,upper bound

O157.5

A

1008-5513(2012)06-0744-05

2011-12-16.

國(guó)家自然科學(xué)基金(61163037,61163054).

劉利群(1977-),碩士,講師,研究方向：圖論及其應(yīng)用.

2010 M SC:05C15