WEI Yi-kun, QIAN Yue-hong

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072 Shanghai, China, E-mail: ykun_wei@sina.com

LATTICE BOLTZMANN METHOD SIMULATIONS FOR MULTIPHASE FLUIDS WITH REDICH-KWONG EQUATION OF STATE*

WEI Yi-kun, QIAN Yue-hong

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072 Shanghai, China, E-mail: ykun_wei@sina.com

(Received February 23, 2011, Revised July 25, 2011)

In this article we state that the compression factor of the Redlich-Kwong Equation Of State (EOS) is smaller than that of van der Waals EOS. The Redlich-Kwong EOS is in better agreement with experimental data on coexistence curves at the critical point than the van der Waals EOS. We implement the Redlich-Kwong EOS in the Lattice Boltzmann Method (LBM) simulations via a pseudo-potential approach. We propose a new force, which can obtain computational stationary and reach larger density ratio. As a result, multi-phase flows with large density ratio (up to 1012in the stationary case) can be simulated. We perform four numerical simulations, which are respectively related to single liquid droplet, vapor-liquid separation, surface tension and liquid coalescence of two droplets.

Redlich-Kwong equation of state, lattice Bhatager-Gross-Krook models, numerical simulations, phase transition

Introduction

In this article a Redlich-Kwong EOS pseudopotential approach is proposed in LBM simulations. A new body force is then introduced in lattice Boltzmann equation. We show that Redlich-Kwong EOS is more suitable for a liquid-vapor system than the van der Waals EOS. The implementation of the Redlich-Kwong EOS in LBM simulations is straightforward. Four numerical simulations are performed, including single liquid droplet, vapor-liquid separation, surface tension and liquid coalescence of two droplets, which demonstrate the applicability of this method.

1. Compression factor and equation of state

There are several equations of state for liquid and vapor. The most classical EOS was proposed by Van der Waals[6], given as

where p is pressure, v is volume and T is temperature. The theoretical critical values of density p, control parameter T and v can be obtained from the following equations

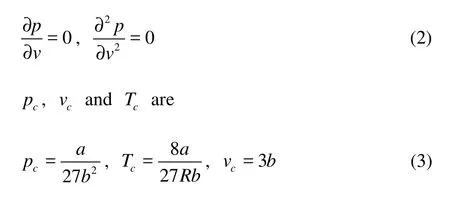
where a and b are constants. The compression factor is defined as

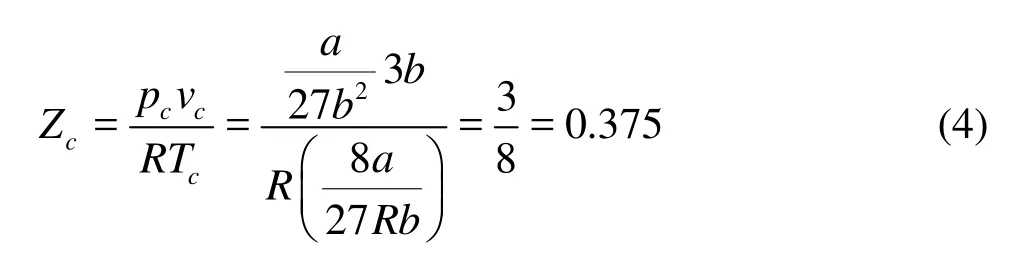
where R is constant. Table 1 shows the compression factors of critical point in common gases. One can find that most of them are between 0.2 and 0.3, which are significantly smaller than the theoretical value 3/8.

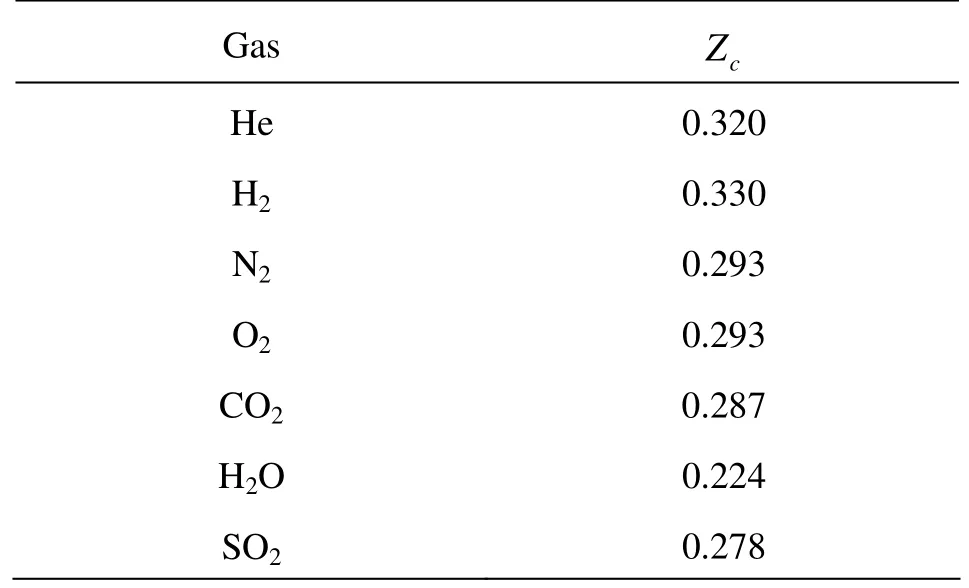
Table 1 The compression factor of critical point different gases[10]

A modified van der Waals EOS is proposed by Redlich and Kwong, namely the Redlich-Kwong EOS

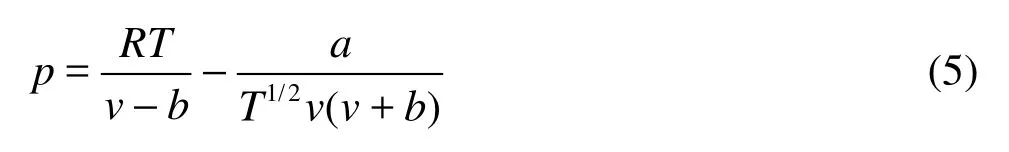
The theoretical value (Zc) is now 1/3. Hence, the compression factor of Redlich-Kwong EOS is closer to real gases than that of van der Waals EOS.

The van der Waals EOS and Redlich-Kwong

EOS are normalized as the following:

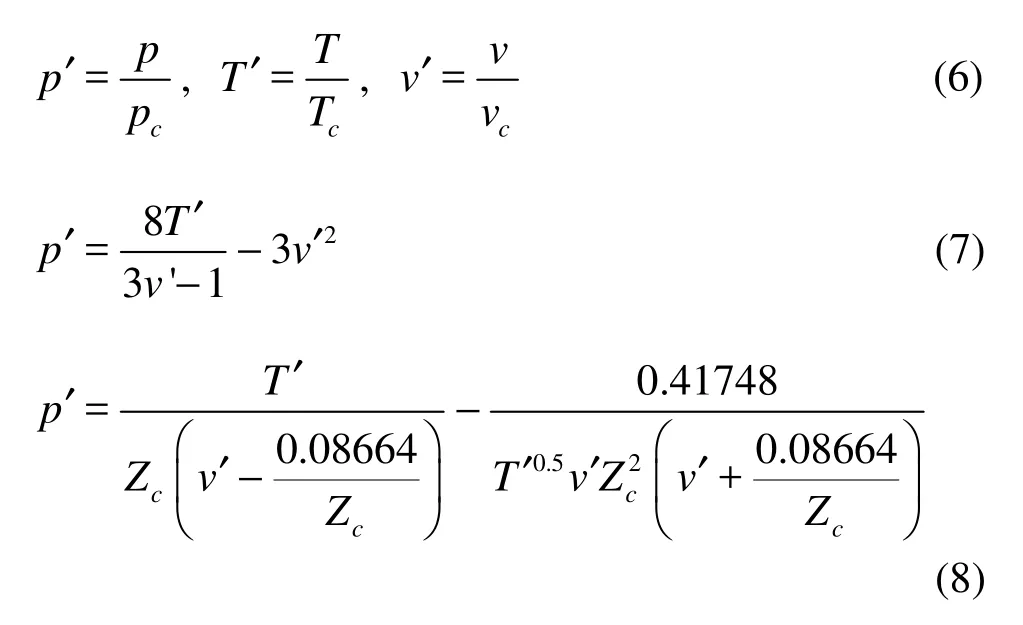
where p′, T′ and v′ are the reduced variables of pressure, temperature and volume.

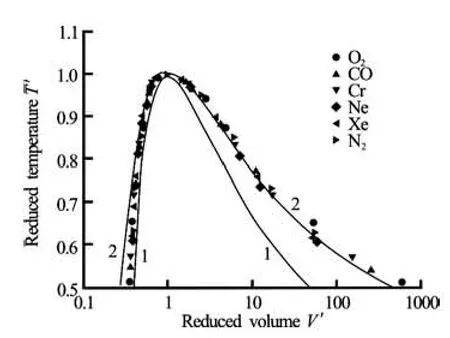
Fig.1 Comparison of the coexistence curves with experimental data: Curve 1 -van der Waals EOS, Curve 2 -Redlich-Kwong EOS, symbols-experimental data[6]

Figure 1 shows the coexistence curves for van der Waals EOS and Redlich-Kwong EOS. For comparison, experimental data from Ref.[6] are also shown as symbols. One can find that the Redlich-Kwong EOS curve is in better agreement with the experimental data. It indicates that the Redlich-Kwong EOS is more suitable for the real gases simulations. We thus propose to implement the Redlich-Kwong EOS in the LBM simulations via a pseudo-potential approach.

2. Lattice Boltzmann method

The LBE with a Bhatnagar-Gross-Krook collision term is written as

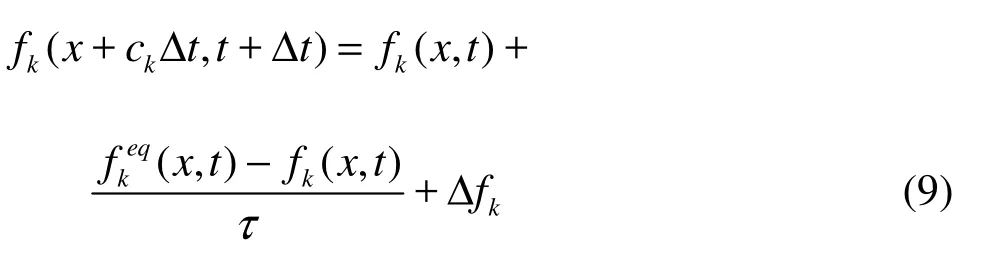
where fkis the particle density with given velocity, τ the collision time, k the index of discrete velocity, Δfka fictitious forcing term describing intera-ctions between neighboring sites, known as body force. It will be explained in more detail later, and ckthe discrete velocity by the following choice:

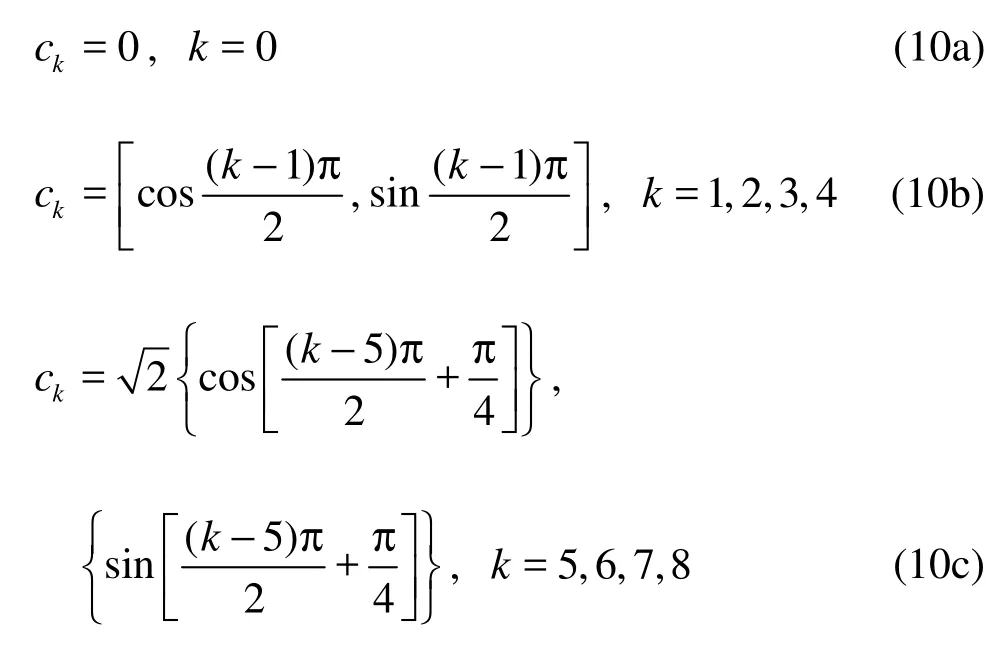
It is sufficient to choose the equilibrium distribution function as

where Δu = F ·Δt /ρ, η is white noise between–0.005 and 0.005, and F is the special mesoscopic forces acting between every pair of neighbor nodes[13]. To describe the phase transition in this model, an attractive force is introduced between every neighbor nodes[5]. For two-dimensional case we have

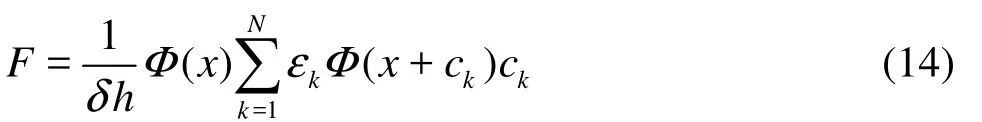
where εk’s are the interaction strength, being 1 for k ={1,2,3,4}and 1/4 for k={5,6,7,8}, The coefficient δ is equal to 2/3 and h is lattice spacing, Φ( x) is the interaction potential function. We choose potential function as

where U = P(ρ,T )?ρθ, and P(ρ,T) is determined by Redlich-Kwong EOS. We rewrite the reduced variables as

where the coefficient q is PcΔt2/ρch2. If we take h / Δt =103m/s , then q≈0.01 for several fluids, e.g., argon[5]. Thus θ ′ = θ(Δ t/h)2=1/3, and h is the lattice spacing.

The Chapman-Enskog expansion is a common tool to derive the macroscopic hydrodynamic equations corresponding to specific LBM. Performing a Taylor expansion of equilibrium distribution functions, we can obtain

Meanwhile, we also obtain the momentum equation

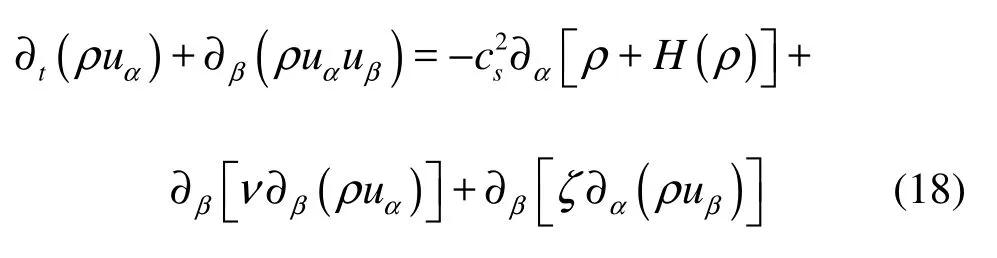
where ν and ζ are shear and bulk viscosities

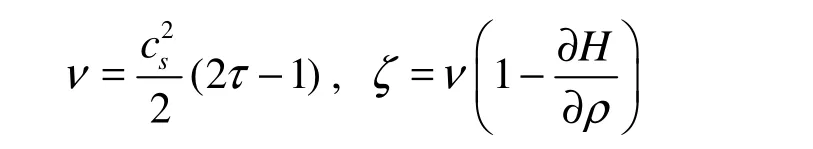
The EOS for this model has the form

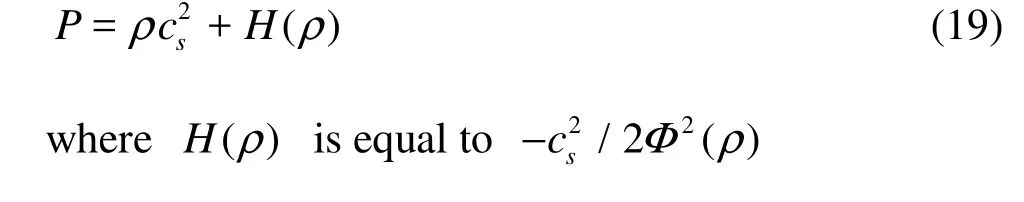
3. Numerical simulations

In this section, we first verify the coexistence curve of the numerical simulation results and the theoretical curve for the Redlich-Kwong EOS. Then we perform four numerical simulations. They are single liquid droplet, vapor-liquid separation, surface tension and liquid coalescence of two droplets.

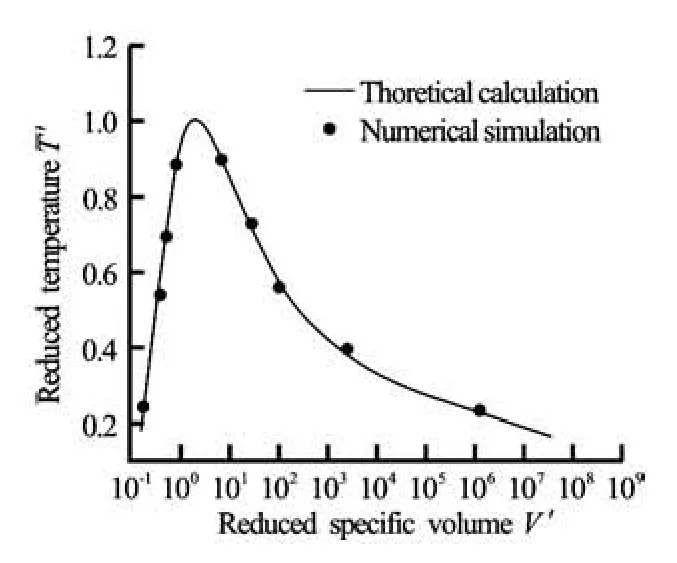
Fig.2 Coexistence curve for the Redlich-Kwong EOS curve and τ=1

3.1 Coexistence curves

Numerical simulations are performed on 100× 100 lattice. Periodic boundary conditions are used in both directions, τ=1 and q=0.01.The system reaches equilibrium after about 105iterations. The density in the bulk phases are then measured for different values of the reduced temperature and plotted in Fig.2. The numerical solution shown as the solid line is found to be in good agreement with simulation results.

Fig.3(a) A snapshot of liquid droplet

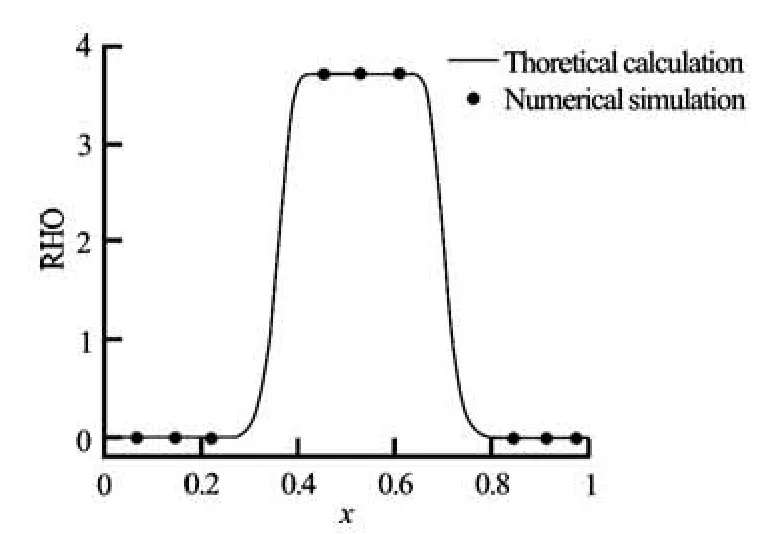
Fig.3(b) Equilibrium density profile normal to a planar interface for a Redlich-Kwong EOS for the reduced temperature T′= 0.19, y=50, τ=1 and q= 0.005

3.2 Single liquid droplet

Fig.4 The evolution of phase separation, t=300, 1 000, 6 000, T′= 0.65 and τ=1

3.3 Vapor-liquid separation

Numerical simulations are performed in two dimensions on a 200×200 lattice nodes. We chooses noise intensity η= 0.01, initial mass densityρ′=1 and particles distributed uniformly. The reduced temperature T′= 0.65, the relaxation time τ=1. The periodic boundary condition is applied in this case. In Fig.4, it is shown the domain morphology at times steps of 300, 1 000 and 6 000. As time evolves, the liquid and vapor are separated gradually. Finally, a big liquid mass can be formed at about center of computational domain.

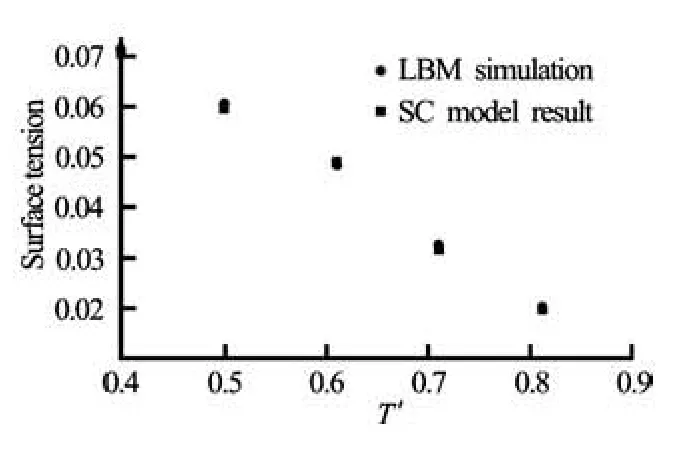
Fig.5 A comparison of surface tension with the theoretical result for the SC model with the surface tension values obtained from the LBM simulations

3.4 Surface tension

Using the Laplace law, we can obtain the surface tension numerically

where Pin′ and Pout′are the reduced pressure inside and outside the bubble. R is a radius of bubble. Theoretical result of the surface tension for LBM was proposed by Shan and Chen, which is calculated from the following equation (SC model)[14]

where c is the lattice constant, D is the dimension of space, n is the direction normal to the interface, and P′ is the reduced pressure. Numerical simulations are performed on 100×100 lattices. Periodic boundary conditions are used in both directions, τ= 1 and q=0.01.The system reaches equilibrium after about 105iterations. Surface tension is then measured for different values of the reduced temperature and plotted in Fig.5. One can find that LBM simulations are in good agreement with the numerical solution of Eq.(21).

3.5 Liquid coalescence of two droplets

Fig.6(a) Snapshots showing coalescence of two droplets at different LBM time-steps, t=1 300, 2 000, 3 000, T′= 0.65, k=0.01 and τ=1

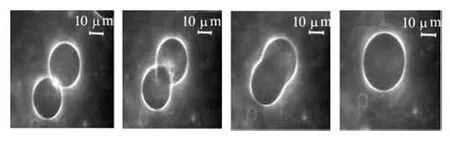
Fig.6(b) Experimental results that is collision of droplets of PIB (430 Pa·s) in PDMS (60 Pa·s), t=0 s, t=10 s, t =12.4 s , t =16.8 s[15]

4. Conclusion

In summary, we have found that the compression factor of the Redlich-Kwong EOS is smaller than that of van der Waals EOS. We have introduced a nonlinear harmonic distribution function about Δu in body force, which remains the stabilization of interfacial tension in liquid-vapor system and obtain large density ratio (up to 1012in the stationary case). We have implemented the Redlich-Kwong EOS in the LBM simulations via a pseudo-potential approach, and illustrated with the cases of single liquid droplet, vapor-liquid separation, surface tension and liquid coalescence of two droplets.

Acknowledgements

The authors wish to acknowledge sincerely to Doctor Xu Hui for very useful discussions.

References

[1] NIE Xiao-bo, SHAN Xiao-wen and CHEN Hu-dong. Thermal lattice Boltzmann model for gases with internal degrees of freedom[J]. Physical Review E, 2008, 77(1): 0357011-0357019.

[2] PRASIANAKIS N. I., KARLIN I. V. Lattice Boltzmann method for thermal flow simulation on standard lattices[J]. Physical Review E, 2007, 76(1): 0167022-0167032.

[3] HE Xiao-yi, DOOLEN G. D. Thermodynamic foundations of kinetic theory and lattice Boltzmann models for multiphase flows[J]. Journal of Statistical Physics, 2002, 107(2): 309-328.

[4] ZHANG Rao-yang, CHEN Hu-dong. Lattice Boltzmann method for simulations of liquid-vapor thermal flows[J]. Physical Review E, 2003, 67(6): 0667111-0667116.

[5] KUPERSHTOKH A. L., MEDVEDEV D. A. and KARPOV D. I. On equations of state in a lattice Boltzmann method[J]. Computers and Mathematics with Applications, 2009, 58(1): 965-974.

[6] YUAN Peng, SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18(4): 0421011-0421019.

[7] YANG Jia-qing, LU De-tang and LI Dao-lun. A new method for boundary condition in lattice Boltzmann method[J]. Chinese Journal of Hydrodynamics, 2009, 24(3): 279-285(in Chinese).

[8] GUO Zhao-li, SHI Bao-chang and ZHAO T. S. et al. Discrete effects on boundary conditions for the lattce Boltzmann equation in simulation microscale gas flow[J]. Physical Review E, 2007, 76(1): 0567041-0567049.

[9] DING Lei, ZHANG Qing-he. 3D lattice Boltzmann simulation of forces on a fixed spherical particle in oscillatory boundary layer flow[J]. Chinese Journal of Hydrodynamics, 2010, 25(3): 391-397(in Chinese).

[10] LI Chun, Zhang Li-yuan. Thermodynamics[M]. Beijing: Higher Education Press, 2002(in Chinese).

[11] QIAN Y. H., D'HUMIèRES D. and LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europe Physics Letter, 1992, 17(6): 479-484.

[12] KUPERSHTOKH A. L. New method of incorporating a body force term into the lattice Boltzmann equation[J]. Proceeding of the Fifth International Workshop. Poitiers, France, 2008, 241-246.

[13] GUO Zhao-li, ZHENG Chu-guang. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review E, 2002, 65(2): 0463081-0463088.

[14] SHI Zi-yuan, YAN Yong-hua and YANG Fan et al. A lattice Boltzmann method for simulation of a threedimensional drop impact on a liquid film[J]. Journal of Hydrodynamics, 2008, 20(3): 267-272..

[15] VERDIER C. The influence of the viscosity ratio on polymer droplet collision in quiescent blends[J]. Journal of Polymer, 2001, 6(1): 6999-7007.

10.1016/S1001-6058(10)60180-1

* Project supported by the Ministry of Education in China (Grant No. IRT0844), the Shanghai Science and Technology Commission Project of Excellent Academic Leaders (Grant No. 11XD1402300).

Biography: WEI Yi-kun (1980-), Male, Ph. D. Candidate

QIAN Yue-hong, E-mail: qian@shu.edu.cn