解亞軍,葉正寅

(西北工業(yè)大學(xué)翼型、葉柵空氣動力學(xué)國家重點(diǎn)實(shí)驗(yàn)室,西安 710072)

0 Introduction

In recent years,many wind tunnel experiments about large aspect ratio aircraft indicate that the test model presences obvious vibration,as shown in Fig.1 which illustrates the wing vibration in the NF-3 low speed wind tunnel of Northwestern Polytechnical University.Thearrow in Fig.1right down region represents the amplitudes of vibration.According to the literature[1-3],it is well known that the reason of producing vibration of large aspect ratio wing mainly comes from elastic vibration of model itselfand vibration of supporting system[4]. Therefore,it is important to be able to improve the precision and reliability of wind tunnel experiments.

Fig.1 The sketch of a wind tunnel model wing vibration圖1 風(fēng)洞模型機(jī)翼振動示意圖

With the development of high-speed computer and numerical computational methods,the computational fluid dynamics(CFD)was introduced in this study.This method possesses some superior characteristics,such as low cost and easy controlling of the properties of fluid.Therefore,in this paper,the CFD approach is employed to study the effect of model vibration on the airfoil flow field by designing several different vibration models[5-7].U-sing the method it is primary found that the elastic vibration of the model may cause the stall incidence ahead.

1 Numerical method

Due to the time consuming of computation on the unsteady flow field,the study of a two-dimensional airfoil is approximately thought as the aerodynamic performance of high aspect ratio wing. Consequently,the evolved infinite interpolation approach is employed to investigate the chosen airfoil-NACA0008 using the C type grid.And the compressible and unsteady N-S equation is described as follow s：

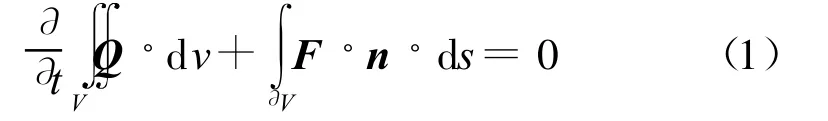
where Q=[ρ,ρ u,ρ v,e]T,in which ρ denotes the fluid density;u and v denote components of the velocity in the directions x and y respectively;e denotes whole internal energy of unit volume;n denotes a unit normal vector of integral boundary;V denotes the integral energy of a unit flow field;?V denotes the boundary of integral region;F denotes flux, which can be classified two categories：non-viscosity FEand viscosity Fv：

In order to improve the reliability of the computation,in the case of unsteady condition,double time method is applied to figure out the unsteady NS equation,where the SST model is employed based on the k-ωequation.In addition,for the sake of comparing the results in different conditions,the computation in different vibration model and different parameters adopts the same grid and viscous coefficient.And when the physical time is advanced, the maximum error advanced about pseudo time in every step is controlled below 10-5.These measures can be used to ensure the computing results reliability.

2 Results and discussion

To simulate the vibration of large aspect ratio aircraft,the NACA0008 airfoil test with the lesser thickness is carried out.According to the low speed in wind tunnel,the Reynolds number of wing is considered to be 1×106,and Mach number is 0.15. In the case of αm=15°,the plunging mode and pitching mode and their various combinations are chosen(showed in the Table 1)to be investigated.

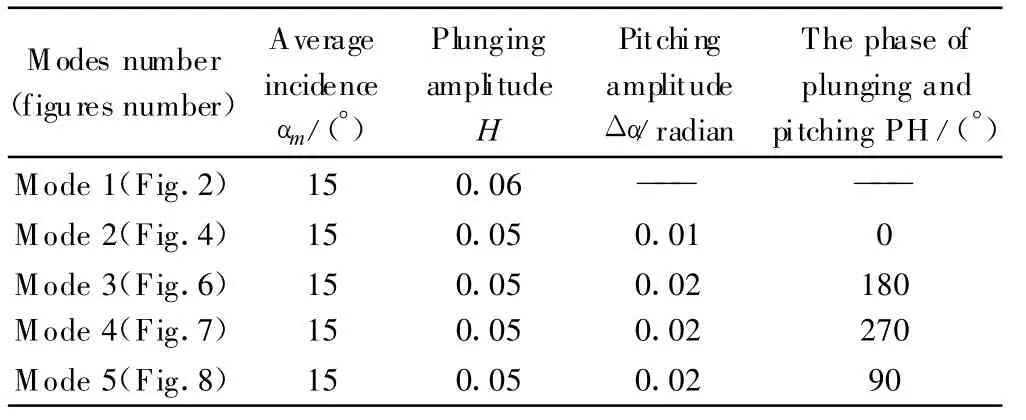
Table 1 Table of calculation modes表1 計(jì)算模態(tài)對應(yīng)表

For the purposes of accurately describing the history variation ofairfoil's lift coefficientand plunging mode with non-dimensional time,the parameter αm=15°,the non-dimensional amplitude (relative airfoil chord length)H=0.06 and k=0.5 are used in the computation.This case is close to the wing tip's vibration of high aspect ratio airplane model which mainly have bending motion.The variation of lift coefficient and plunging movements with non-dimensional time is illustrated in Fig.2(Mode 1),where the curve of lift coefficient with non-dimensional time is above,and the curve of plunging movements of airfoil with non-dimensional time is below.It can be seen from the results that when the airfoil is at rest,which corresponds to the non-dimensional time T less than 150,the separate vortex around the airfoil's flow field doesn't appear.In addition,it is evident that when airfoil begins to vibrate, which corresponds to the non-dimensional time T＞150, the oscillation amplitude of lift coefficient presents periodical change.However the reason of this variation is mainly from the unsteady plunging movements of airfoil.Consequently,when the airfoil descends to the lower points,the small separated vortex is emerged in the back of airfoil,as shown in Fig.3.

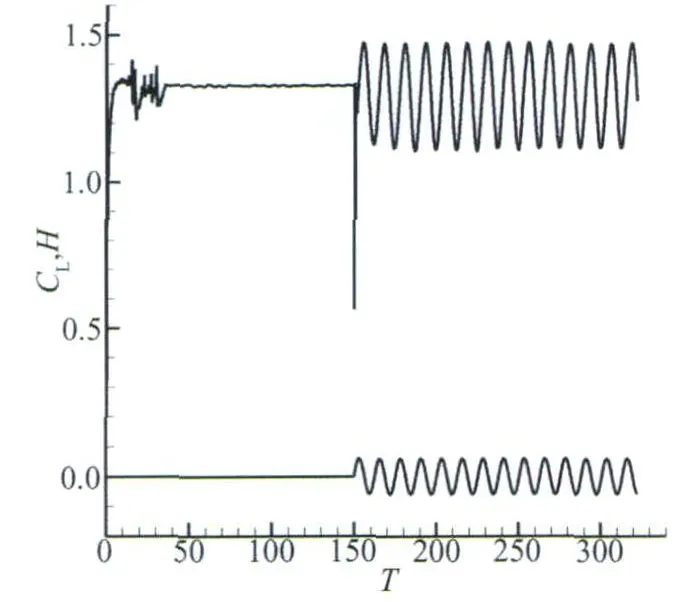
Fig.2 Curve of the airfoil's lift coefficient and plunge vibration with time圖2 翼型升力系數(shù)和沉浮位移隨時(shí)間振動曲線

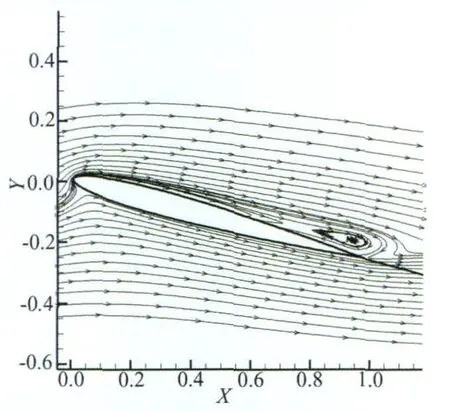
Fig.3 The flow field of the airfoil's plunge vibration at the lowest position圖3 翼型沉浮振動到最低位置的流場

Generally,aircraft wing will perform bend vibration and torsion vibration at the same time when the center of gravity of airfoil model along the chord from the leading edge is not consistent with the elastic axis,which is corresponding with pitching and plunging movement of the airfoil.The variation of lift with non-dimensional time is shown in Fig.4 (Mode 2)for αm=15°,H=0.05 and Δα=0.01 radian(corresponding to angle 0.573°).The curve that is upper in Fig.4 represents the variation of lift coefficient with non-dimensional time,the middle curve denotes the variation of pitching angle with non-dimensional time,the lower curve shows the variation of plunging displacement with non-dimensional time.It is evident that the top surface of airfoilpresents the regularlarge scale shedding process.Furthermore,the shedding frequency of separate vortex is coincident with the vibration frequency.This is attributed to the combination of airfoil plunging and pitching vibration.Also,it can be seen that the phase of pitching vibration is consistent with the plunging movements,namely the maximum value of pitching is correspondence with the peak of lift-dow n movements.T he evidence of this phenomenon represents the contribution from the fact that the airfoil elastic axis locates behind the center of gravity of airfoil.Moreover,when the phase of pitching vibration is opposite to that of the plunging movements,namely the minimum value of pitching is correspondence with the peak of the plunging movements.This is attributed to the fact that the airfoil elastic axis locates the front of center of gravity of airfoil.Fig.5 shows the severe separation flow field of the airfoil's vibration.It is evident that even though the vibration magnitude of pitching reaches 0.02 radians,the severe separation vortex unsteady shedding as shown in Fig.5 does not appear in the flow field of airfoil.Fig.6(Mode 3) presents the variation of lift coefficient for αm=15°, H=0.05 and Δα=0.02 radians.

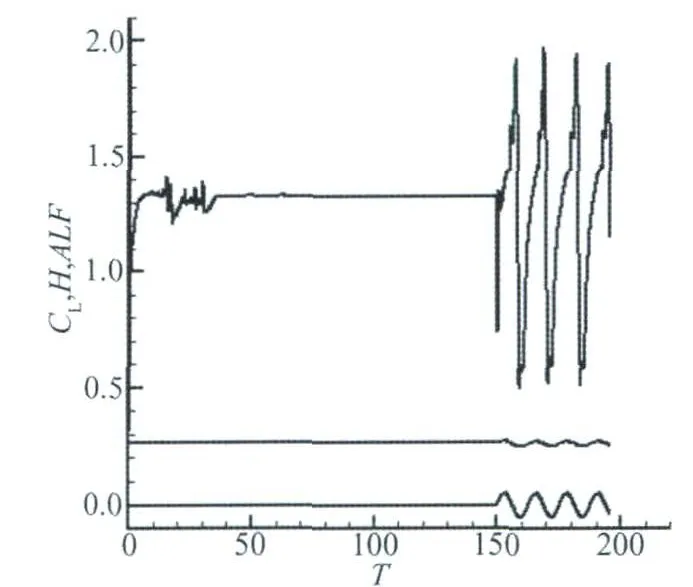
Fig.4 Curve of the airfoil's lift coefficient and plunge and pitch vibration with time(PH=0°)圖4 翼型升力系數(shù)和沉浮俯仰位移隨時(shí)間振動曲線(PH=0°)

To demonstrate the effect of different phases on the calculation,Fig.7(Mode 4)shows the variation of airfoil lift with the non-dimensional time in pitching vibration lagging behind the 270°phase of plunging movements for αm=15°,H=0.05 and Δα=0.02 radians.It is demonstrated that the severe separation vortex doesn't emerge in the flow field of airfoil and the oscillation magnitude of lift coefficient resulted from the unsteady vibration attenuation obviously.

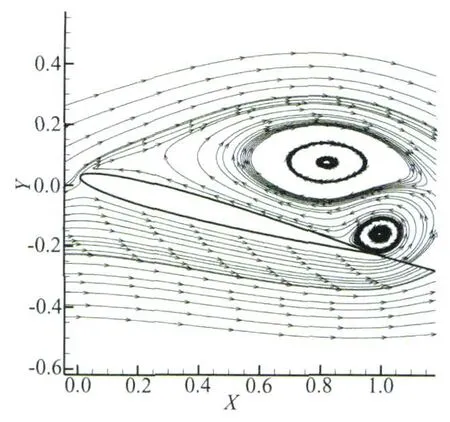
Fig.5 Severe separation flow field of the airfoil's vibration corresponding to Fig.4圖5 與圖4對應(yīng)的翼型大旋渦分離流場

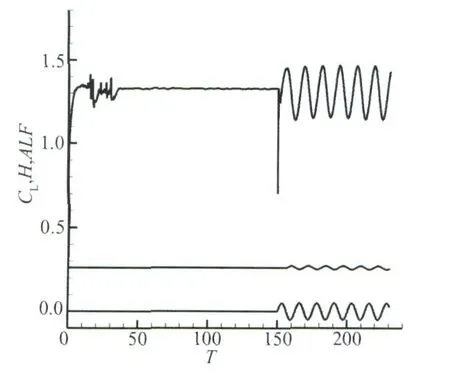
Fig.6 Curve of the airfoil's lift coefficient and plunge and pitch vibration with time(PH=180°)圖6 翼型升力系數(shù)和沉浮俯仰位移隨時(shí)間振動曲線(PH=180°)

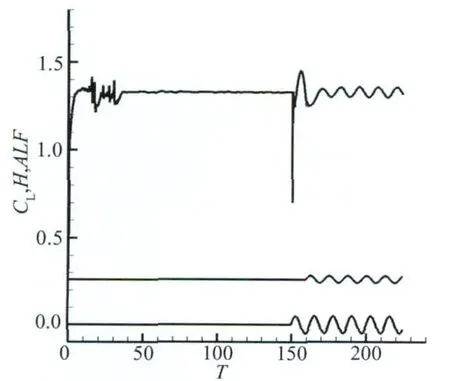
Fig.7 Curve of the airfoil's lift coefficient and plunge and pitch vibration with time(PH=270°)圖7 翼型升力系數(shù)和沉浮俯仰位移隨時(shí)間振動曲線(PH=270°)

Based on the mode above,the unsteady process with pitching vibration lagging behind 90°phase of plunging movements is given in Fig.8(Mode 5).It is clear that the severe separation vortex unsteady shedding presents.Additionally,the oscillation magnitude of lift coefficient is greater than that of same phase,as shown in Fig.9.

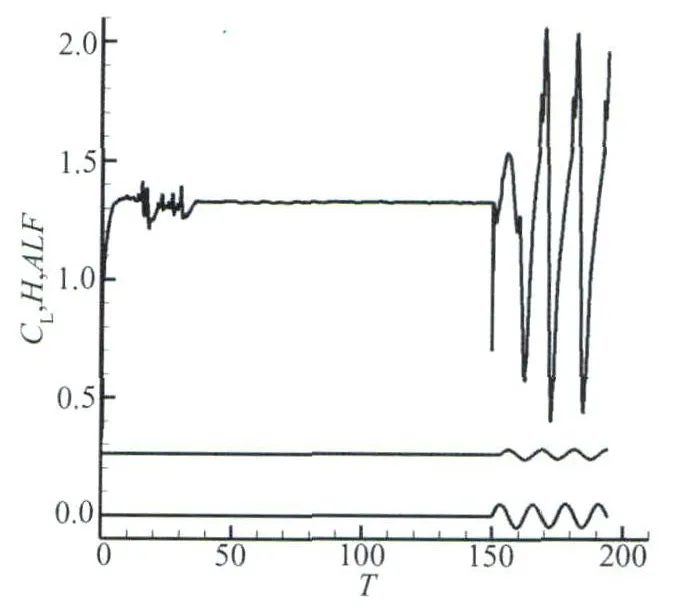
Fig.8 Curve of the airfoil's lift coefficient and plunge and pitch vibration with time(PH=90°)圖8 翼型升力系數(shù)和沉浮俯仰位移隨時(shí)間振動曲線(PH=90°)

Fig.9 More severe separation flow field of the airfoil's vibration corresponding to Fig.8圖9 與圖8對應(yīng)的翼型大旋渦分離流場

3 Conclusions

In this paper the numerical method CFD for the simulation of the interaction between model vibration and the flow field of airfoil in wind tunnel experiments is discussed.The study focuses on the flow field of airfoil at high incidence.Combination of different phase between two vibrations(the plunging vibration and pitching vibration)of the airfoil is also studied.The basic conclusions that can be drawn from the studies are as below：(1)When the different vibration lags behind the different phase,the response of separation of airfoil flow field is different.When the phase between the pitching vibration and plunging movements is consistent or little difference,the effect of pitching vibration and plunging movements on the flow field is marked,which corresponds to the wind tunnel test model at the center of gravity of airfoil along the chord from the leading edge that is in front of the elastic axis.When the phase angle difference between the pitching vibration and lift-down movements is 270°,the effect of pitching vibration and plunging movements on the flow field is weaker, which corresponds to the wind tunnel test model at the center of gravity of airfoil along the chord from the leading edge that is behind the elastic axis.(2) For the low speed wind tunnel test models,particularly,in the design of large aspect ratio wind tunnel test models,their wings must be provided enough strength.In addition,the influence of model vibration on the wind tunnel models must be considered in the experiments,especially,the effect of variation near the stall incidence is visible.

[1]BUEHRLE R D,YOUNG C P Jr,BALAKRISHNA S, et al.Experimental study of dynamic interaction between model support structure and a high speed research model in the national transonic facility[R].AIAA Paper 94-1623,1994.

[2] EDWARDS J W.National transonic facility model and tunnel vibrations[R].AIAA Paper 97-0345,1997.

[3] LIVNE E.Controlled-motion models for wind tunnel unsteady aerodynamic loads identification on deforming configurations：a multidisciplinary challenge[R].AIAA Paper 2000-1485,2000.

[4] WHITING R J,DELAMORE-SUTCLIFFE D W,GREENWELL D.Experimental and numerical study of gust loads on stall flutter initiative[R].AIAA Paper 2005-5097,2005.

[5] 葉正寅,謝 飛.彈性振動對翼型失速迎角附近流場的影響[J].航空學(xué)報(bào),2006,27(6)：1028-1032.

[6] 葉正寅.彈性振動翼對流場和氣動性質(zhì)的影響[C].近代空氣動力學(xué)研討會論文集(祝賀莊逢甘院士八十華誕),北京,2005.

[7] 葉正寅,王 剛,楊永年.變形機(jī)翼非定常繞流的數(shù)值模擬[C].第十屆計(jì)算流體力學(xué)會議論文集,綿陽, 2000.