馮迎春, 鄭 列

(湖北工業(yè)大學(xué) 理學(xué)院, 武漢 430068)

FENG Ying-chun, ZHENG Lie

( School of Science , Hubei University of Technology ,Wuhan 430068 , China)

一般約束非線性規(guī)劃問題的光滑牛頓法

馮迎春, 鄭 列

(湖北工業(yè)大學(xué) 理學(xué)院, 武漢 430068)

用改進(jìn)的光滑NCP函數(shù)替代了文 [1,2]中的弱互補(bǔ)函數(shù), 提出了一種新的光滑牛頓法, 從而實(shí)現(xiàn)了一般約束優(yōu)化問題的KKT條件到非線性方程組之間的完全等價轉(zhuǎn)化, 且將文[3]中提出的求解無約束最優(yōu)化問題的修正BFGS 方法加以改進(jìn), 應(yīng)用于求解一般的約束最優(yōu)化問題, 避免了計算Hesse矩陣工作量較大的問題, 并在一定的條件下證明了該算法的全局收斂性.

NCP函數(shù); 牛頓法; KKT條件

A Smooth Newton Method for General Constrained Nonlinear Optimization Problem

FENG Ying-chun, ZHENG Lie

( School of Science , Hubei University of Technology ,Wuhan 430068 , China)

Abstract:In this paper, an improved smooth NCP function replaces the weak complementary functions in the literature [1,2] and a new smooth Newton method is proposed, therefore the KKT conditions of the constraint optimization is transformed into an equivalent nonlinear equations. the Modified BFGS Algorithm proposed in literature [3] is applied to solve the general constrained optimization problem, the main advantages of this method lies that its iterative matrix is positive definite, while avoiding the calculation of the workload of Hesse matrix, and it is proved that the algorithm is global convergence under certain conditions.

Key words:NCP function; Newton method; KKT conditions

引言

考慮一般約束非線性規(guī)劃問題(簡稱為GNP問題)

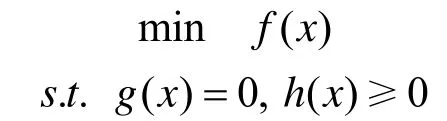
其中g(shù)( x)=(g1( x),…,gl( x ))T:→Rl,h( x)=(hl+1(x),…,hl+m(x ))T:→和f:→均為連續(xù)可微函數(shù), E={1,2,…,l},I={l+1,l+2,…,l+m}.

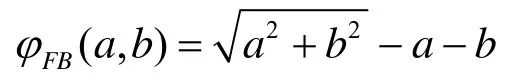
1 算法及理論基礎(chǔ)

為了把約束規(guī)劃問題轉(zhuǎn)化為無約束規(guī)劃問題, 引入廣義Lagrange函數(shù)

下面考慮基于改進(jìn)的光滑NCP函數(shù)和廣義Lagrange函數(shù)的光滑牛頓法, 其算法如下:

Step1 給定初值: x1∈Rn, λ1∈Rl, μ1∈Rm為給定正數(shù), 參數(shù)η, γ∈(0,1), ε≥0, θ∈[0,1], 初始對稱正定矩陣B1, k:=1.

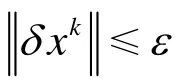
Step3 取αk為{1,η ,η2,…}中滿足不等式φ(zk+αkδk)≤φ(zk)+γαkH(zk)δk的最大值.

Step4 令zk+1=zk+αkδk.

Step5計算Bk+1, k:=k+1, 轉(zhuǎn)Step2.

在算法中, 我們采用BFGS公式來計算Bk+1, 其修正公式為:

2 收斂性分析

若u=0, 由式(6)及假設(shè)2)可知v=0,w=0. 若u≠0, 由于Bk為正定矩陣及式(6), 所以

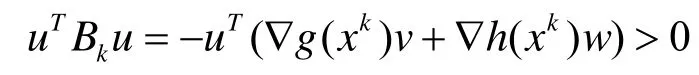
由(7)、(10)及(11)可知uTB u恒為0, 故與上式相矛盾, 從而假設(shè)u≠0不成立, 因此(u, v, w)=0. 所以ω為

kk可逆陣.

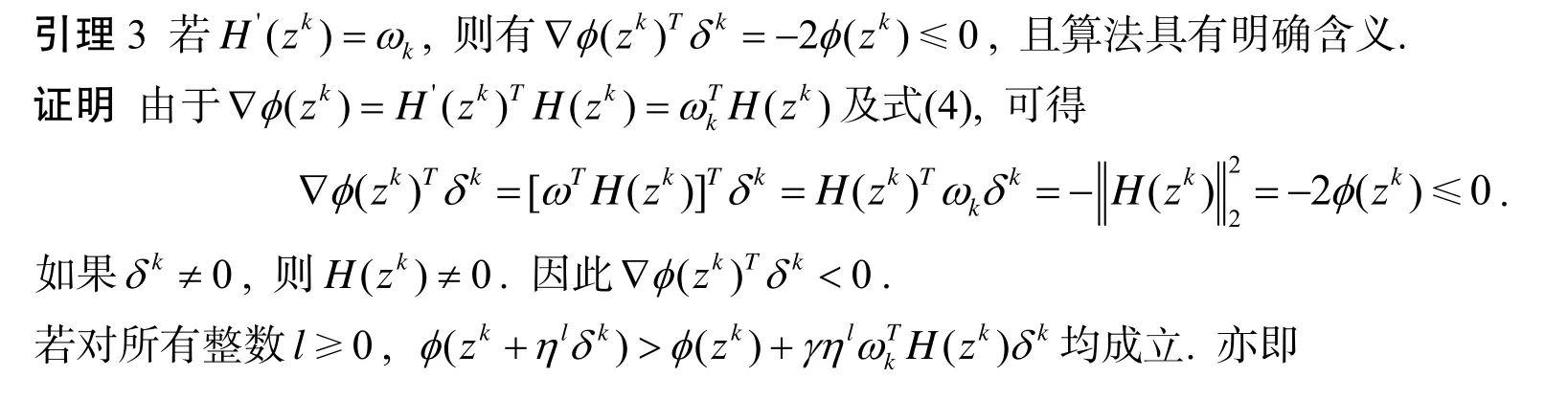
[1] 桂勝華, 張 倩, 邢 麗. 弱互補(bǔ)函數(shù)的拉格朗日—擬牛頓法[J]. 上海第二工業(yè)大學(xué)學(xué)報, 2005, 12(5): 21～27

[2] 桂勝華, 周 巖. 拉格朗日—擬牛頓法解約束非線性規(guī)劃問題[J]. 同濟(jì)大學(xué)學(xué)報, 2007, 4(4): 556～561

[3] 焦寶聰. 一類改進(jìn)BFGS算法及其收斂性分析[J]. 數(shù)學(xué)的實(shí)踐與認(rèn)識, 1999, 29 (2): 143～149

[4] 王秀國, 邱菀華. 一種解決不等式約束優(yōu)化的光滑牛頓法[J]. 運(yùn)籌與管理, 2004, 10(5): 62～66

[5] 孫守霞, 劉 偉. 解非線性不等式約束優(yōu)化問題的非精確光滑牛頓法[J]. 魯東大學(xué)學(xué)報, 2007, 23(1): 19～22

[6] 陳寶林. 最優(yōu)化理論與算法[M]. 北京: 清華大學(xué)出版社, 2005

[7] 袁亞湘. 非線性優(yōu)化計算方法[M]. 北京: 科學(xué)出版社, 2008

O221.2

A

1672-5298(2010)01-0020-04

2009-09-26

馮迎春(1983- ), 女, 湖南長沙人, 湖北工業(yè)大學(xué)理學(xué)院碩士研究生. 主要研究方向: 最優(yōu)化理論