XIE Jia, DENG Bing-mao

(1School of Mathematics and Information Science, Guangzhou University, Guangzhou, Guangdong,510006, P.R. China; 2School of Financial Mathematics and Statistics, Guangdong University of Finance, Guangzhou, Guangdong, 510521, P.R. China)

Abstract: Let k be a positive integer, let h(z)0 be a holomorphic functions in a domain D, and let F be a family of zero-free meromorphic functions in D, all of whose poles have order at least l. If, for each f ∈F, P(f)(z)?h(z) has at most k +l ?1 distinct zeros(ignoring multiplicity) in D, where P(f)(z)=f(k)(z)+a1(z)f(k?1)(z)+···+ak(z)f(z) is a differential polynomial of f and aj(z)(j =1,2,··· ,k) are holomorphic functions in D, then F is normal in D.

Key words: Meromorphic Function; Normality; Zero-free

§1. Introduction and Main Result

Let D be a domain in C and F a family of meromorphic functions in D. F is said to be normal in D (in the sense of Montel) if each sequence {fn} ?F has a subsequence {fnj}which converges locally uniformly in D with respect to the spherical metric, to a meromorphic function or ∞.

We define that P(f)(z) is a differential polynomial of f, where P(f)(z) = f(k)(z) +a1(z)f(k?1)(z)+···+ak(z)f(z) and aj(z)(j =1,2,··· ,k) are holomorphic functions in D.

In 1959, Hayman[4]proved the following result.

Theorem ALet f be a nonconstant meromorphic function in C and k be a positive integer. Then f or f(k)?1 has at least a zero. Moreover, if f is transcendental, then f or f(k)?1 has infinitely many zeros.

The normality corresponding to Theorem A was conjectured by Hayman[5]and confirmed by Gu[3]in 1979.

Theorem BLet F be a family of zero-free meromorphic functions in a domain D and k be a positive integer. If f(k)1 for each f ∈F, then F is normal in D.

In 1986, Yang[9]extended Theorem B as follows.

Theorem CLet F be a family of zero-free meromorphic functions in a domain D and h(0) be a holomorphic function in D. If, for each f ∈F, f0 and f(k)h for z ∈D, then F is normal in D.

Chang[1]improved Theorem B and proved the following result.

Theorem DLet F be a family of zero-free meromorphic functions in a domain D and k be a positive integer. If, for each f ∈F, the function f(k)?1 has at most k distinct zeros(ignoring multiplicity) in D, then F is normal in D.

Deng, Fang and Liu[2]extended Theorem C and proved the following result.

Theorem ELet F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic function in D, and let k be a positive integer. If, for each f ∈F,f(k)?h has at most k distinct zeros (ignoring multiplicity) in D, then F is normal in D.

In 2013, Liu, Deng and Yang[6]replaced f(k)(z)?h(z) by P(f)(z)?h(z), and proved the following result.

Theorem FLet F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic function in D, and let k be a positive integer. If, for each f ∈F,P(f)(z)?h(z) has at most k distinct zeros (ignoring multiplicity) in D, then F is normal in D.

In this paper, we consider about the order of poles of f. Here is our main result.

Theorem 1Let k be a positive integer,let h(0)be a holomorphic functions in a domain D,and let F be a family of zero-free meromorphic functions in D,all of whose poles have order at least l. If, for each f ∈F, the function P(f)(z)?h(z) has at most k+l ?1 distinct zeros(ignoring multiplicity) in the domain D, then F is normal in D.

ExampleSuppose that F ={fn(z)=1/nzl:n ≥(k+l?1)!+1},that P(fn)(z)=that D = {z : |z| < 1} and that h(z) = 1/(z ?1)k+l, where k is a positive integer. Then, for each fn∈F, the function P(fn)(z)?h(z) has k+l distinct zeros (ignoring multiplicity) in D,but F is not normal in D. This shows that the condition in Theorem 1 that P(f)?h has at most k+l ?1 distinct zeros (ignoring multiplicity) in D is best possible.

Corollary 1Let F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic functions in D, and let k be a positive integer. If, for each f ∈F,all of whose poles have order at least l, and the function f(k)(z)?h(z) has at most k+l ?1 distinct zeros (ignoring multiplicity) in D, then F is normal in D.

Corollary 2Let F be a family of zero-free meromorphic functions in a domain D, and k be a positive integer. If, for each f ∈F, all of whose poles have order at least l, and the function f(k)has at most k+l ?1 fixed points (ignoring multiplicity) in D, then F is normal in D.

§2. Some Lemmas

Lemma 1[7]Let α ∈R satisfying ?1 < α < ∞and let F be a family of zero-free meromorphic functions in a domain D. If F is not normal at z0∈D,then there exist points zj(∈D)→z0, functions fj∈F, and positive numbers ρj→0+, such that gj(ξ)=f(zj+ρjξ)converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ).

Lemma 2[8]Let f be a transcendental meromorphic function,let a(0)be a polynomial,and let k be a positive integer. If f0, then f(k)?a has infinitely many zeros.

Lemma 3Let f be a nonconstant zero-free rational function,all of whose poles have order at least l, let a(0) be a polynomial and let k be a positive integer. Then f(k)?a has at least k+l distinct zeros (ignoring multiplicity) in C.

ProofSuppose that

since f is a nonconstant zero-free rational function, f is not a polynomial, and hence has at least one finite pole with order at least l. Further, by calculation, the function f(k)?a has at least one zero in C. Thus, we can write

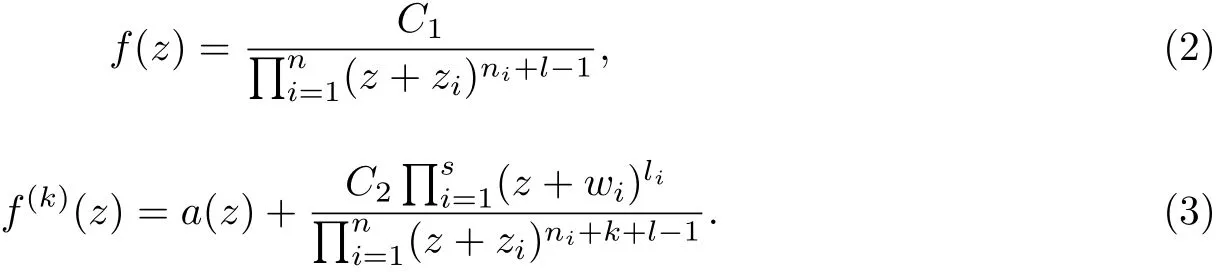
Where C1and C2are nonzero constants, m, n, s, li, mi, and ni≥1(1 ≤i ≤n) are positive integers, the vi(when 1 ≤i ≤m) are distinct complex numbers, and the zi(when 1 ≤i ≤n)and wi(when 1 ≤i ≤s) are distinct complex numbers. Set

Then by induction, we deduce from (2) that

where Pkis a polynomial of deg Pk=(n ?1)k. Thus, by (1), (3), and (4),

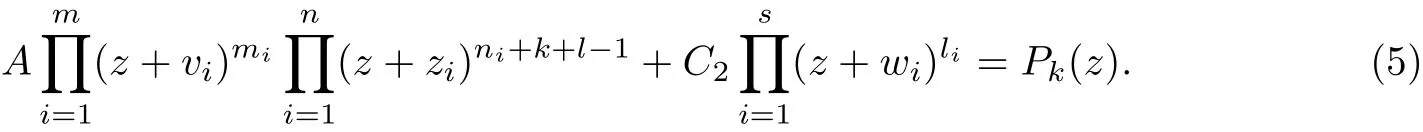
and C2=?A. Thus by (5), we get

where Q(t)=t(n?1)kPk(1/t)/A is a polynomial of deg Q ≤(n ?1)k, and it follows that

Logarithmic differentiation of (6) shows that

We consider two cases.

Case 1If deg a=M =0then a is constant. Thus (7) may be rewritten:

Comparing the coefficients of tj(j =0,1,··· ,N +k+n(l ?1)?2), we deduce that

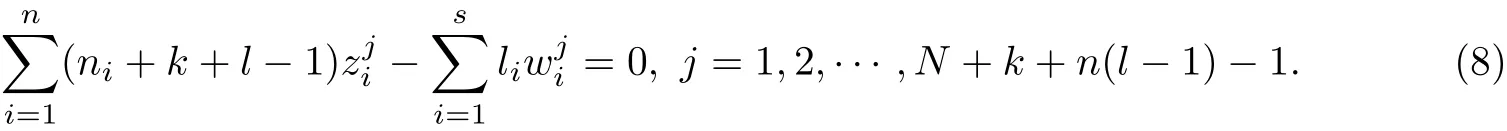
Let zn+i=wi(1 ≤i ≤s).

Subcase 1.10 for each i ∈{1,··· ,n+s}. Noting that0 and using (8), we deduce that the system of linear equations

has a nonzero solution

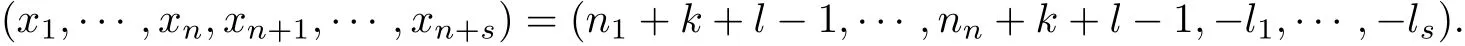
If n+s ≤N +k+n(l ?1), then by Cramers rule,

where 0 ≤j ≤N+k+n(l ?1)?1. However, the determinant is a Vandermonde determinant,so cannot be 0, which is a contradiction. Hence, we conclude that n+s>N +k+n(l ?1). It follows from this and the inequality N =≥n that s ≥k+l.

Subcase 1.2There exist i ∈{1,··· ,n+s} such that zi= 0, for all. Without loss of generality, we assume that zn+s=0, then it follows from (8) that

has a nonzero solution. Next, using the same argument as in Subcase 1.1, we deduce that s ≥k+l.

Case 2deg a=M ≥1. Comparing the coefficients of tj(j =0,1,··· ,M+N+k+n(l ?1)?2) in (7), we deduce that

Set

Obviously, S2∩S3=?.

Subcase 2.1S1∩S2=and S1∩S3=. Let zn+1= vi(1 ≤i ≤m), and zn+m+i=wi(1 ≤i ≤s).

Subsubcase 2.1.10 for all i ∈{1,...,n+m+s}. Since

it follows from (9) that

has a nonzero solution. Then using the same argument as Subcase 1.1,we deduce that s ≥k+l.

Subsubcase 2.1.2There exist i ∈{1,··· ,n+m+s} such that zi=0, for all. Without loss of generality, we assume that zn+m+s=0, then it follows from (9) that

has a nonzero solution. Next,using the same argument as Subcase 1.2,we deduce that s ≥k+l.

Subcase 2.2S1∩S2= ?and S1∩S3= ?. Without loss of generality, we may assume that S1∩S2={v1,v2,··· ,vM1}, where vi=zi(1 ≤i ≤M1). Let M3=m ?M1, and set

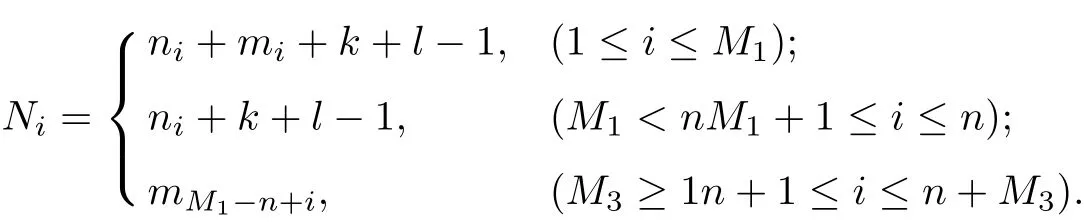
If M3≥1, then set zn+i=vM1+i(1 ≤i ≤M3). In the subcase, (9) may be rewritten:

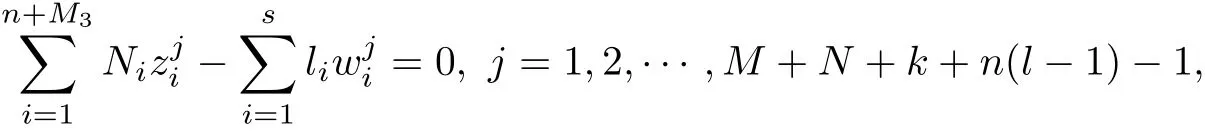
where 0 ≤M3≤m ?1. Using the argument of Subcase 2.1, we deduce that s ≥k+l.

Subcase 2.3S1∩S2= ?and S1∩S3?. Without loss of generality, we may assume that S1∩S3={v1,v2,··· ,vM2}, where vi=wi(1 ≤i ≤M2). Let M4=m ?M2, and set

If M4≥1, then set ws+i=vM2+i(1 ≤i ≤M4). In the subcase, (9) may be rewritten that

where 0 ≤M4≤m ?1. Using the argument of Subcase 2.1, we deduce that s ≥k+l.

Subcase 2.4S1∩and S1∩S3Without loss of generality, we may assume that S1∩S2= {v1,v2,··· ,vM1}, S1∩S3= {w1,w2,··· ,wM2}, where vi= zi(1 ≤i ≤M1)and wi=vM1+i(1 ≤i ≤M2). Set M5=m ?M2?M1, and set

If M5≥1, then set zn+i=vM1+M2+i(1 ≤i ≤M5). In the subcase, (9) may be rewritten that

where 0 ≤M5≤m ?2. Using the argument of Subcase 2.1, we deduce that s ≥k+l.

This completes the proof of Lemma 3.

§3. Proof of Theorem 1

At first we show that F is normal in the set D= {z ∈D : h(z). Suppose that F is not normal at z0∈D. We may assume that D =?and h(z0)=1. By Lemma 1, there exist fn∈F, zn→z0and ρn→0+such that gn(ξ)=+ρnξ) converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ), all of whose poles have order at least l.

We claim that g(k)?1 has at most k+l ?1 distinct zeros. Suppose that g(k)?1 has k+l distinct zeros ξj(1 ≤j ≤k+l). Obviously, we have1. Then by

uniformly in compact subsets of C disjoint from the poles of g. And by Hurwitzs theorem, for n sufficiently large, there exist points ξn,j→ξj(j = 1,2,··· ,k +l) , such that P(f)(zn+ρnξn,j) = h(zn+ρnξn,j). However, P(f)(z)?h(z) has at most k+l ?1 distinct zeros in D and zn+ρnξn,j→z0, which is a contradiction, and proves our claim.

However, by Lemma 2, we know that g is a rational function. But this contradicts Lemma 3. This contradiction shows that F is normal in.

We now prove that F is normal at{z :h(z)=0}. Making standard normalizations,we may assume that h(z)=zmb(z) (z ∈?), where m ≥1, b(0)=1 and h(z)0 for 0<|z|<1. Let

Suppose not. Then by Lemma 1, there exist Fn∈F∞, zn→0 and ρn→0+such that gn(ξ)=ρ?knFn(zn+ρnξ)converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ).

Next we distinguish two cases.

Case 1There is a subsequence of zn/ρn, we still denote as zn/ρn, such that zn/ρn→α,where α is a finite complex number. Let ?g(ξ)=g(ξ ?α), then uniformly in compact subsets of C disjoint from the poles oObviously,0, and the pole of ?g at ξ =0 has order at least m. Now

uniformly in compact subsets of C disjoint from the polesand all of the poles of G have multiplicity at least l. Since ?g has a pole of order at least m at ξ = 0, then G(0)0, and noting that

For

uniformly in compact subsets of C. And

That is

So

uniformly in compact subsets of C disjoint from the poles of G.

Since P(f)(z)?h(z) has at most k+l ?1 distinct zeros in D, as discussed as the above,we get that G(k)(ξ)?ξmhas at most k+l ?1 distinct zeros in C. However, by Lemma 2 and Lemma 3, G(ξ)≡C, where C is a constant. Then we have Gn(ξ)=fn(ρnξ)C, and

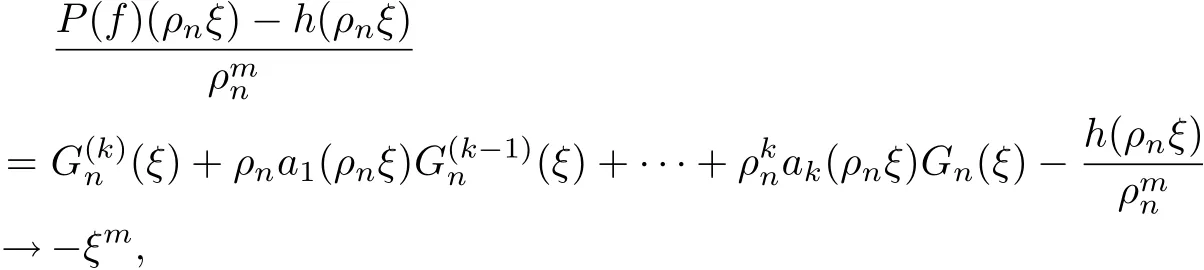
uniformly in compact subsets of C disjoint from the poles of G.

Recall {fn} is normal in, but not normal at z = 0, and since, we can deduce that there exist εn→0, such that fn(εn) = ∞, where |εn| = min{|f?1n(∞)|}. We claim that εn/ρn→∞. Otherwise, suppose that εn/ρn→α. Then

A contradiction. Then εn/ρn→∞.

It is easy to get that P?(Qn)(z)?zmb(εnz)has at most k+l ?1 distinct zeros in C. Obviously,Qn(0. It follows from the above that {Qn} is normal inSince Qnis holomorphic in ?, and0, by the Maximum Principle Theorem, it is easy to obtain that {Qn} is normal in ?, then {Qn} is normal in C.

Next, there exist a subsequence of Qn, we still denote as Qn, such that Qn(z) converges locally spherically uniformly in C to a meromorphic function Q(z) or ∞. Since Qn0 and Qn(0) = Gn(0)(ρn/εn)k+m→0, we get Q(z)0 by Hurwitzs theorem. But Qn(1) = ∞, so Q(1)=∞, a contradiction.

Case 2 There exist a subsequence of zn/ρn, we still denote as zn/ρn, such that zn/ρn→∞. By simple calculation,

where

Note that all of the poles of gnhave order at least l at the point zn+that is ξ?zn/ρn, and zn/ρn→∞. By gnconverging locally spherically uniformly in C to g, we see that all of the poles of g have multiplicity at least l. So we have

Note that

disjoint from the poles of g(ξ) and

So

uniformly in compact subsets of C disjoint from the poles of g.

Thus,we proved that F∞is normal at z =0. It remains to prove that F is normal at z =0.Since F∞is normal at z =0 and F(0)=∞for each , F ∈F∞there exist 0<δ <1 such that|F(z)|≥1 for each F ∈F∞and each z ∈?(0,δ). And0, hence 1/f is analytic in ?(0,δ)for all f ∈F. Therefore, for all f ∈F, we have

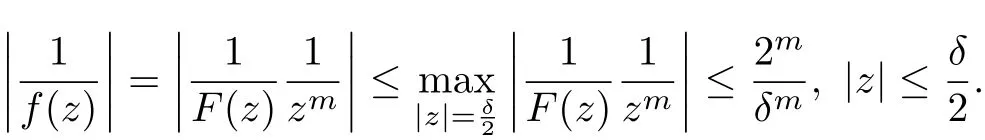
By the Maximum Principle and Montels Theorem, F is normal at z =0. Thus F is normal in D.

This completes the proof of Theorem 1.